Modelul Ising este un exemplu particular de sistem termodinamic și este un sistem model pentru înțelegerea tranzițiilor de fază. Știți cum atât de mulți biologi petrec atât de mult timp cu niște amărâte de muște de fructe? Ei bine, fizicienii petrec foarte mult timp cu modelul Ising. După cum ne spune în mod util profesorul Raghu, acesta este Drosophila tranzițiilor de fază.

Personal, nu sunt cel mai mare fan al analogiei sale, deoarece cred că muștele de fructe sunt scârboase. Să sperăm că modelul Ising nu va fi prea scârbos.

Motivație

De ce ar trebui să petrecem atât de mult timp vorbind despre modelul Ising?

• Este surprinzător de util pentru a ne ajuta să ne gândim la tot felul de comportamente legate de tranzițiile de fază. De exemplu:

  • modelul Ising prezintă rupere de simetrie în faza de temperatură joasă (despre care tocmai am vorbit)

  • are un „punct critic” special la o temperatură bine definită (la care am făcut aluzie în diagrama de fază a apei)

  • alte caracteristici bogate.

• Este unul dintre puținele modele exact rezolvabile în care putem calcula efectiv mărimile termodinamice și le putem interpreta.

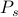  • În general, calcularea mărimilor termodinamice este dificilă pentru că trebuie să însumăm mulți termeni. Amintiți-vă de la primul nostru curs de termoficare că vă puteți gândi la un sistem de echilibru ca la un ansamblu de multe stări , fiecare ponderată cu propria probabilitate . În acest cadru, mărimile termodinamice pe care le observați corespund mediilor asupra ansamblului. În particular, dacă doriți să găsiți media ansamblului unei anumite observabile 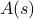, trebuie să găsiți suma 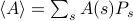, unde suma se desfășoară peste toate stările posibile. Problema cu acest lucru, după cum vă amintiți, este că numărul de stări ale unui sistem termodinamic se scalează exponențial cu numărul de particule! Chiar și pentru un sistem de dimensiuni moderate, există pur și simplu prea multe stări pentru ca un calculator să calculeze explicit media – cu atât mai puțin un sistem termodinamic în care 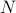este de ordinul .

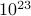  • Așa că trebuie să ”fim isteți” pentru a calcula funcția de partiție, și ar trebui să fim recunoscători pentru sistemele exact rezolvabile!

• Modelul Ising este simplu, dar poate fi aplicat la un număr surprinzător de sisteme diferite.

  • Aceasta este prima noastră mostră de universalitate – o caracteristică a fenomenelor critice în care aceeași teorie se aplică la tot felul de tranziții de fază diferite, fie în lichide și gaze, fie în magneți sau supraconductori sau orice altceva. Fizicienii iubesc acest tip de comportament general deoarece sugerează un fel de ordine mai profundă în lumea noastră haotică.

Definiția modelului Ising

Modelul Ising este un model matematic care nu corespunde unui sistem fizic real. Este o rețea imensă (pătrată) de situsuri, în care fiecare situs poate fi într-una din cele două stări. Etichetăm fiecare sit cu un indice , iar cele două stări le numim și . Pentru a spune că cel de-al -lea sit este în starea , scriem .

Acum, această definiție este lamentabil de abstractă și nefizică, așa că pentru noi, fizicienii, este extrem de util să avem în minte un sistem real, astfel încât să ne putem referi la ceva explicit și să ne construim o intuiție fizică. Iată câteva sisteme fizice pe care le-ar putea reprezenta modelul Ising:

• Un magnet. Fiecare loc reprezintă un anumit „spin” din material (un electron neperecheat???), și este dacă spinul este îndreptat în jos sau dacă spinul este îndreptat în sus. Fiecare dintre spini se comportă ca un mini-iman cu propriul său mini-moment magnetic; dacă toți spinii sunt aliniați, atunci întreaga rețea de spini se comportă ca un magnet mare cu un moment magnetic net macroscopic.

• Un aliaj; să zicem, alamă. Fiecare dintre site reprezintă un atom din rețea; reprezintă un atom de cupru în acel site; reprezintă zincul.

• Un ”gaz de rețea”. Fiecare dintre situri reprezintă posibila localizare a unei particule; înseamnă că acel sit este gol, iar înseamnă că acel sit este ocupat de o particulă.

• Rețelele vortexurilor bacteriene??

Deocamdată, ne vom gândi la modelul Ising ca la un model pentru un magnet. Este un model extrem de simplificat și de jucărie al unui magnet, cu siguranță, dar analogia cu magnetul poate totuși să ne ajute să ne ghidăm intuiția fizică prețioasă.

Punând laolaltă hamiltonianul

O întrebare firească pe care trebuie să ne-o punem cu privire la acest model de magnet de tip Mickey-mouse este ce energie are acesta. Pentru a fi mai preciși, dorim să scriem o funcție care să reprezinte energia fiecărei configurații posibile (a.k.a. microstate) a spinilor din magnet. După cum știm, această funcție energetică se numește hamiltonian.

În modelul Ising, hamiltonianul include două tipuri de interacțiuni:

• termenul de câmp extern. După cum ne amintim din mecanica cuantică, un câmp magnetic extern poate împărți energiile stării de spin-down și spin-up, astfel încât una este mai mare în energie și cealaltă este mai mică.

  • Mărimea lui reprezintă cât de puternic este câmpul, deci vă spune cât de mult este mai mare în energie un spin decât celălalt.

  • Semnul lui vă spune dacă este preferat spinul up sau spinul down.

  • Din moment ce fiecare spin individual resimte câmpul extern, trebuie să adunăm toate sitele pentru a găsi contribuția totală la energie.

• termenul de interacțiune dintre spinii vecini – poate că vor să se alinieze unul cu celălalt și să puncteze în aceeași direcție, poate că vor să se antialinieze și să puncteze în moduri diferite. Din punct de vedere fizic, ne putem imagina că această interacțiune apare pentru că fiecare spin din magnet este propriul său mini-dipol magnetic care își stabilește propriul câmp magnetic, iar vecinii săi pot simți acest câmp magnetic.

  • Mărimea lui ne spune cât de puternic sunt cuplate între ele spinii vecini – cât de mult vor să se (anti)alinieze. Din punct de vedere fizic, intensitatea cuplării spin-spin ar putea depinde de distanța dintre ei în lattica magetului, de exemplu.

  • Semnul lui vă spune dacă vecinii preferă să se alinieze sau să se antialinieze. (Termenul tehnic pentru aceasta este feromagnetic sau, respectiv, antiferomagnetic). Din punct de vedere fizic, dacă un material este unul sau altul (sau niciunul) depinde de detaliile exacte de mecanică cuantică ale modului în care interacționează spinii.

  • Din moment ce interacțiunea spin-spin apare între doi spini, trebuie să adunăm peste perechile de situri pentru a găsi interacțiunea sa totală la energie.

Mai multe despre termenul de interacțiune

O întrebare firească despre termenul de interacțiune spin-spin este care spini sunt cuplați cu care spini?

Dacă ne întoarcem din nou la imaginea fizică a magnetului și ne concentrăm asupra unui anumit spin, ne-am aștepta ca puterea interacțiunii spin-spin să fie mai puternică pentru spinii apropiați și mai slabă pentru spinii îndepărtați. Dependența exactă de distanță a interacțiunilor spin-spin este probabil destul de complicată pentru magneții reali.

Pentru modelul Ising, facem cea mai simplă ipoteză posibilă pentru natura acestei interacțiuni spin-spin:

Câteva comentarii:

• Într-o rețea pătrată de dimensiuni, fiecare sit are 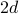vecini mai apropiați: stânga și dreapta într-o dimensiune, sus și jos odată ce se adaugă a doua dimensiune, etc…

• Supunem că interacțiunea este izotropă – toți vecinii sunt tratați în mod egal, indiferent de direcție.

• Deseori vorbim despre interacțiunile între vecinii cei mai apropiați ca despre energia unei legături care unește două situri de rețea.

• Când adunăm peste perechi adiacente de situri, simbolic, scriem mici paranteze unghiulare în jurul indicilor pentru a reprezenta ”cel mai apropiat vecin”.

O consecință plăcută a interacțiunilor celui mai apropiat vecin este că atunci când găsim energia totală a unei anumite configurații de spini, în loc să adunăm peste toate perechile posibile de situri, adunăm numai peste perechile de situri care sunt adiacente între ele.

Acum că am discutat toate aceste lucruri, suntem gata să scriem expresia reală a hamiltonianului. (Am vrut să explic și să interpretez fizica înainte de a scrie hamiltonianul, astfel încât simbolurile să aibă un fel de sens.)

Hamiltonianul modelului Ising

Hamiltonianul modelului Ising poate fi scris ca

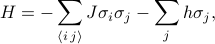
unde reprezintă interacțiunea spin-spin, reprezintă câmpul extern, iar 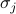sunt spinii individuali pe fiecare dintre locurile rețelei. Prima sumă se referă la toate perechile de situri de rețea vecine (denumite și legături); ea reprezintă interacțiunile dintre spini. A doua sumă se referă la toate site-urile de rețea; reprezintă câmpul extern care încearcă să alinieze toți spinii într-o singură direcție.

Continuați cu termodinamica modelului Ising.

.