Convoluția nedorită este o problemă inerentă în transferul de informații analogice. De exemplu, toate următoarele pot fi modelate ca o convoluție: încețoșarea imaginii într-o cameră foto tremurândă, ecourile în convorbirile telefonice la mare distanță, lățimea de bandă finită a senzorilor și electronicii analogice etc. Deconvoluția este procesul de filtrare a unui semnal pentru a compensa o convoluție nedorită. Scopul deconvoluției este de a recrea semnalul așa cum era înainte de a avea loc convoluția. Acest lucru necesită, de obicei, cunoașterea caracteristicilor deconvoluției (de exemplu, răspunsul la impuls sau la frecvență). Acest lucru se poate deosebi de deconvoluția oarbă, în care caracteristicile convoluției parazite nu sunt cunoscute. Deconvoluția oarbă este o problemă mult mai dificilă care nu are o soluție generală, iar abordarea trebuie să fie adaptată la aplicația particulară.

Deconvoluția este aproape imposibil de înțeles în domeniul timpului, dar destul de simplă în domeniul frecvenței. Fiecare sinusoidă care compune semnalul inițial poate fi modificată în amplitudine și/sau fază pe măsură ce trece prin convoluția nedorită. Pentru a extrage semnalul original, filtrul de deconvoluție trebuie să anuleze aceste modificări de amplitudine și fază. De

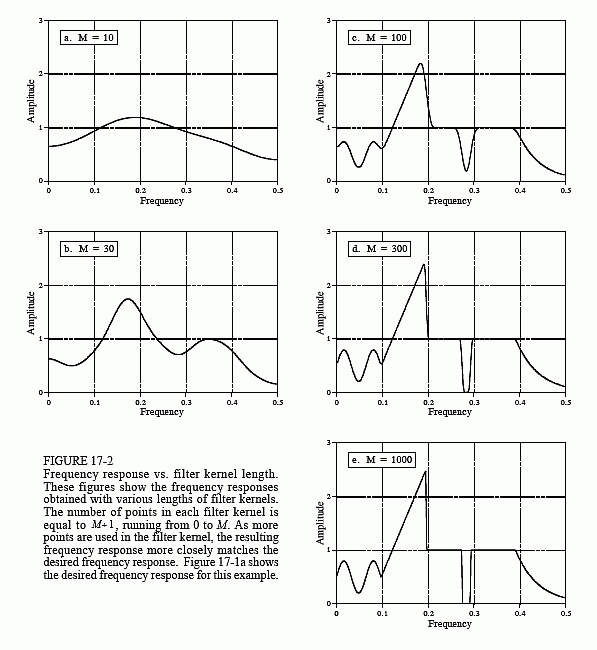
exemplu, dacă convoluția modifică amplitudinea unui sinusoid cu 0,5 cu o schimbare de fază de 30 de grade, filtrul de deconvoluție trebuie să amplifice sinusoidul cu 2,0 cu o schimbare de fază de -30 de grade.

Exemplul pe care îl vom folosi pentru a ilustra deconvoluția este un detector de raze gamma. Așa cum este ilustrat în Fig. 17-3, acest dispozitiv este compus din două părți, un scintilatorși un detector de lumină. Un scintilator este un tip special de material transparent, cum ar fi iodura de sodiu sau germanatul de bismut. Acești compuși transformă energia din fiecare rază gamma într-o scurtă explozie de lumină vizibilă. Această lumină

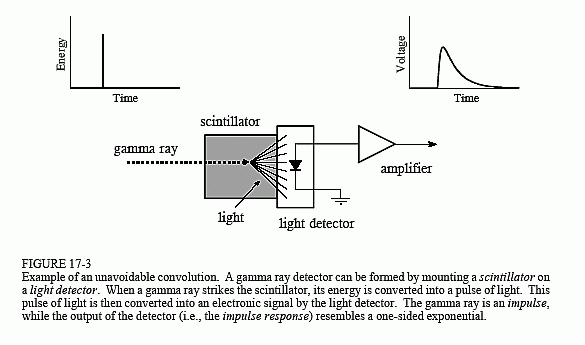
este apoi transformată într-un semnal electronic de către un detector de lumină, cum ar fi o fotodiodă sau un tub fotomultiplicator. Fiecare impuls produs de detectorseamănă cu o exponențială unilaterală, cu o anumită rotunjire a colțurilor. Această formă este determinată de caracteristicile scintilatorului utilizat. Atunci când o rază gama își depune energia în scintilator, atomii din apropiere sunt excitați la un nivel energetic mai ridicat. Acești atomi se deexcinează aleatoriu, fiecare dintre ei producând un singur foton de lumină vizibilă. Rezultatul net este un impuls luminos a cărui amplitudine scade pe parcursul a câteva sute de nanosecunde (pentru iodura de sodiu). Având în vedere că sosirea fiecărei raze gamma este un impuls, impulsul de ieșire de la detector (adică exponențiala unilaterală) este răspunsul la impuls al sistemului.

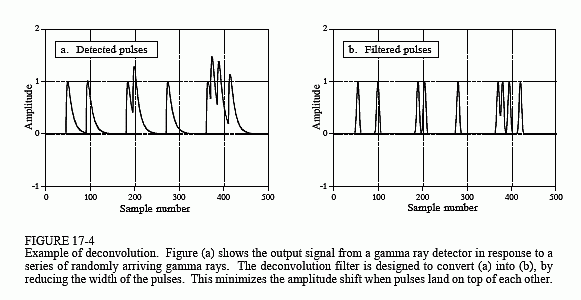
Figura 17-4a arată impulsurile generate de detector ca răspuns la razele gamma care sosesc aleatoriu. Informația pe care am dori să o extragem din acest semnal de ieșire este amplitudinea fiecărui impuls, care este proporțională cu energia razei gamma care l-a generat. Aceasta este o informație utilă, deoarece energia poate spune lucruri interesante despre locul pe unde a fost raza gamma. De exemplu, poate furniza informații medicale despre un pacient, poate indica vârsta unei galaxii îndepărtate, poate detecta o bombă în bagajele unei companii aeriene etc.

Toate ar fi în regulă dacă s-ar detecta doar o rază gamma ocazională, dar de obicei nu este cazul. După cum se arată în (a), două sau mai multe impulsuri se pot suprapune,modificând amplitudinea măsurată. Un răspuns la această problemă este deconvoluția semnalului de ieșire al detectorului, făcând impulsurile mai înguste, astfel încât să se producă mai puțină suprapunere. În mod ideal, am dori ca fiecare impuls să semene cu impulsul original. După cum probabil bănuiți, acest lucru nu este posibil și trebuie să ne mulțumim cu un impuls care are o lungime finită, dar semnificativ mai scurtă decât impulsul detectat. Acest obiectiv este ilustrat în Fig. 17-4b.

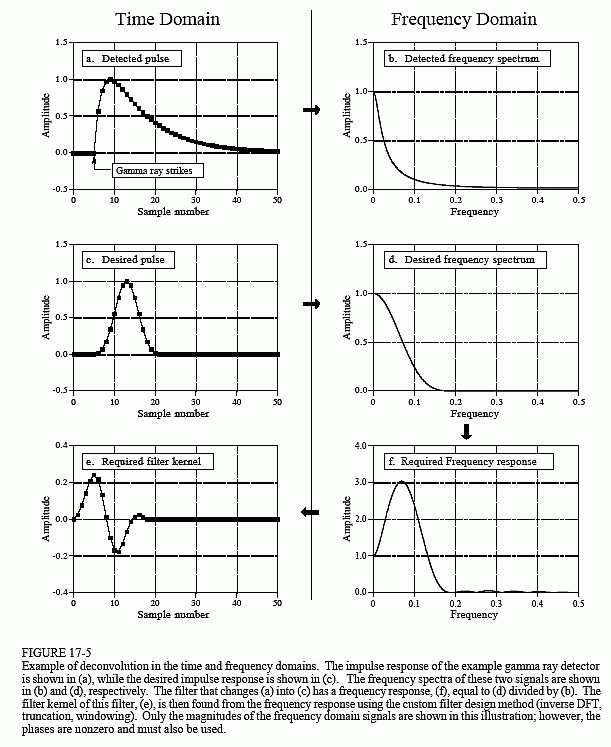
Chiar dacă semnalul detectorului are informația sa codificată în domeniul timpului, o mare parte din analiza noastră trebuie să se facă în domeniul frecvenței, unde problema este mai ușor de înțeles. Figura 17-5a este semnalul produs de detector(ceva ce cunoaștem). Figura (c) este semnalul pe care dorim să-l avem (de asemenea, ceva ce știm). Acest impuls dorit a fost ales în mod arbitrar pentru a avea aceeași formă ca o fereastră Blackman, cu o lungime de aproximativ o treime din cea a impulsului original. Scopul nostru este de a găsi un nucleu de filtru, (e), care, atunci când este convoltat cu semnalul din (a), produce semnalul din (c). Sub formă de ecuație: dacă a * e = c, și date fiind a și c, găsimde.

Dacă aceste semnale ar fi fost combinate prin adunare sau înmulțire în loc deconvoluție, soluția ar fi fost ușoară: scăderea este folosită pentru a „de-aduna”, iar împărțirea este folosită pentru a „de-multiplica”. Convoluția este diferită; nu există o operație inversă simplă care să poată fi numită „deconvoluție”. Convoluția este prea complicată pentru a fi anulată prin manipularea directă a semnalelor din domeniul temporal.

Din fericire, această problemă este mai simplă în domeniul frecvenței. Amintiți-vă,convoluția într-un domeniu corespunde cu înmulțirea în celălalt domeniu. Referindu-ne din nou la semnalele din Fig. 17-5: dacă b × f = d, și date fiind b și d, găsiți f. Aceasta este o problemă ușor de rezolvat: răspunsul în frecvență al filtrului, (f), estespectrul de frecvență al impulsului dorit, (d), împărțit la spectrul de frecvență al impulsului detectat, (b). Deoarece impulsul detectat este asimetric, acesta va avea o fază diferită de zero. Aceasta înseamnă că trebuie utilizată o diviziune complexă (adică o magnitudine & fază împărțită la o altă magnitudine & fază). În cazul în care ați uitat, capitolul 9 definește modul în care se efectuează o diviziune complexă a unui spectru cu altul. Sâmburele de filtru necesar, (e), se găsește apoi din răspunsul în frecvență prin metoda filtrului personalizat (IDFT, decalare, trunchiere, &multiplicare cu o fereastră).

Există limite la îmbunătățirea pe care o poate oferi deconvoluția. Cu alte cuvinte, dacă deveniți lacomi, lucrurile se vor prăbuși. A deveni lacom în acest exempluînseamnă a încerca să faci impulsul dorit excesiv de îngust. Să ne uităm la ceea ce se întâmplă. Dacă impulsul dorit este făcut mai îngust, spectrul său de frecvență trebuie să conțină mai multe componente de înaltă frecvență. Deoarece aceste componente de înaltă frecvență sunt la o amplitudine foarte mică în impulsul detectat, filtrul trebuie să aibă un câștig foarte mare la aceste frecvențe. De exemplu, (f) arată că unele frecvențe trebuie să fie înmulțite cu un factor de trei pentru a obține pulsul dorit în (c). În cazul în care impulsul dorit este mai îngust, câștigul filtrului de deconvoluție va fi și mai mare la frecvențe înalte.

Problema este că erorile mici sunt foarte neiertătoare în această situație. De exemplu,dacă o anumită frecvență este amplificată cu 30, când este necesară doar 28, semnalul deconvoluționat va fi probabil un dezastru. Atunci când deconvoluția este împinsă la niveluri mai mari de performanță, caracteristicile convoluției nedorite trebuie să fie înțelese cu mai multă acuratețe și precizie. Există întotdeauna necunoscute în aplicațiile din lumea reală, cauzate de răufăcători precum: zgomotul electronic, deriva de temperatură, variația dintre dispozitive etc. Aceste necunoscute stabilesc o limită la cât de bine va funcționa deconvoluția.

Chiar dacă convoluția nedorită este perfect înțeleasă, există totuși un factor care limitează performanța deconvoluției: zgomotul. De exemplu, majoritatea convoluțiilor nedorite iau forma unui filtru trece-jos, reducândamplitudinea componentelor de înaltă frecvență din semnal. Deconvoluția corectează acest lucru prin amplificarea acestor frecvențe. Cu toate acestea, dacă amplitudinea acestor componente scade sub nivelul zgomotului inerent al sistemului, informațiile conținute în aceste frecvențe se pierd. Nici o cantitate de procesare a semnalului nu poate să o recupereze. Este pierdută pentru totdeauna. Adios! La revedere! Sayonara! Încercarea de a recupera aceste date nu va face decât să amplifice zgomotul. Ca un caz extrem, amplitudinea unor frecvențe poate fi complet redusă la zero. Acest lucru nu numai că șterge informația, dar va încerca să facă ca filtrul de deconvoluție să aibă un câștig infinit la aceste frecvențe. Soluția: concepeți un filtru de deconvoluție mai puțin agresiv și/sau impuneți limite la cât de mult câștig este permis la oricare dintre frecvențe.

Cât de departe se poate merge? Cât de lacom este prea lacom? Acest lucru depinde în totalitate deproblema pe care o atacați. Dacă semnalul se comportă bine și are un zgomot redus, probabil că se poate face o îmbunătățire semnificativă (gândiți-vă la un factor de 5-10). În cazul în care semnalul se schimbă în timp, nu este deosebit de bine înțeles sau este zgomotos, nu veți reuși la fel de bine (gândiți-vă la un factor de 1-2). O deconvoluție reușită implică foarte multe teste. Dacă funcționează la un anumit nivel, încercați să mergeți mai departe; veți ști când se prăbușește. Nici o cantitate de muncă teoretică nu vă va permite să ocoliți acest proces repetitiv.

Deconvoluția poate fi aplicată, de asemenea, la semnale codificate în domeniul frecvenței. Un exemplu clasic este restaurarea înregistrărilor vechi ale celebrului cântăreț de operă,Enrico Caruso (1873-1921). Aceste înregistrări au fost realizate cu echipamente foarte primitive în comparație cu standardele moderne. Cea mai importantă problemă este reprezentată de rezonanțele cornului tubular lung de înregistrare folosit pentru a colecta sunetul. Ori de câte ori cântărețul se întâmplă să atingă una dintre aceste frecvențe de rezonanță, zgomotul înregistrării crește brusc. Deconvoluția digitală a îmbunătățit calitatea subiectivă a acestor înregistrări prin

reducerea punctelor tari din muzică. Vom descrie doar metoda generală;pentru o descriere detaliată, consultați lucrarea originală: T. Stockham, T. Cannon, andR. Ingebretsen, „Blind Deconvolution Through Digital Signal Processing”,Proc. IEEE, vol. 63, Apr. 1975, pp. 678-692.

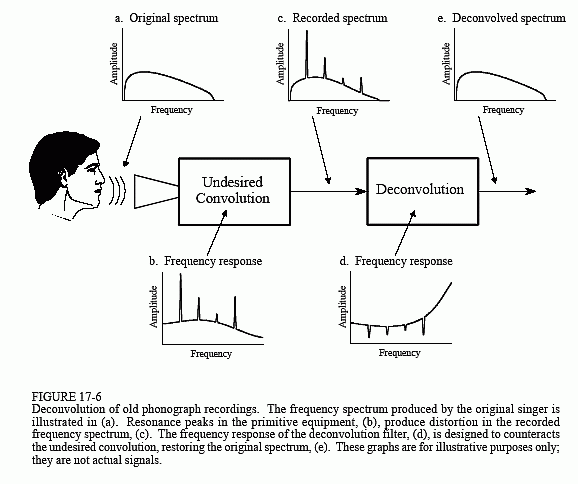
Figura 17-6 prezintă abordarea generală. Spectrul de frecvență al semnalului audio original este ilustrat în (a). Figura (b) prezintă răspunsul în frecvență al echipamentului de înregistrare, o curbă relativ netedă, cu excepția câtorva vârfuri de rezonanță ascuțite. Spectrul semnalului înregistrat, ilustrat în (c), este egal cu spectrul adevărat, (a), înmulțit cu răspunsul neuniform la frecvență, (b). Scopul deconvoluției este acela de a contracara această deconvoluție nedorită. Cu alte cuvinte, răspunsul în frecvență al filtrului de deconvoluție,(d), trebuie să fie inversul lui (b). Altfel spus, fiecare vârf din (b) este anulat de o scădere corespunzătoare din (d). Dacă acest filtru ar fi perfect proiectat, semnalul rezultat ar avea un spectru, (e), identic cu cel al originalului.

Iată care este șmecheria: echipamentul original de înregistrare a fost de mult aruncat, iar răspunsul său în frecvență, (b), este un mister. Cu alte cuvinte, aceasta este o problemă de deconvoluție oarbă; având în vedere doar (c), cum putem determina (d)?

Problemele de deconvoluție oarbă sunt de obicei atacate prin efectuarea unei estimări sau a unei presupuneri cu privire la parametrii necunoscuți. Pentru a trata acest exemplu, se presupune că spectrul mediu al muzicii originale se potrivește cu spectrul mediu al aceleiași muzici interpretate de un cântăreț din zilele noastre folosind echipament modern. Spectrul mediu se găsește prin tehnicile de la capitolul 9: se împarte semnalul într-un număr mare de segmente, se ia DFT a fiecărui segment, se convertește în formă polară și apoi se calculează media mărimilor împreună. În cel mai simplu caz, răspunsul de frecvență necunoscut este considerat ca fiind spectrul mediu al înregistrării vechi, împărțit la spectrul mediu al înregistrării moderne. (Metoda utilizată de Stockham et al. se bazează pe o tehnică mai sofisticată, numită procesare homomorfă, care oferă o estimare mai bună a caracteristicilor sistemului de înregistrare).