de Marco Taboga, PhD
Funcția indicatoare a unui eveniment este o variabilă aleatoare care ia valoarea 1 când evenimentul se produce și valoarea 0 când evenimentul nu se produce. Funcțiile indicatoare sunt adesea folosite în teoria probabilităților pentru a simplifica notația și pentru a demonstra teoreme.

Definiție
În cele ce urmează este o definiție formală.
Definiție Fie  un spațiu de eșantionare și
un spațiu de eșantionare și  un eveniment. Funcția indicatoare (sau variabila aleatoare indicatoare) a evenimentului
un eveniment. Funcția indicatoare (sau variabila aleatoare indicatoare) a evenimentului  , notată cu
, notată cu  , este o variabilă aleatoare definită după cum urmează:
, este o variabilă aleatoare definită după cum urmează: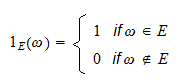
În timp ce indicatorul unui eveniment  este de obicei notat cu
este de obicei notat cu  , uneori este notat și cu
, uneori este notat și cu unde
unde  este litera greacă Chi.
este litera greacă Chi.
Exemplu Aruncăm un zar și unul dintre cele șase numere de la 1 la 6 poate apărea cu fața în sus. Spațiul de probă este Definiți evenimentul
Definiți evenimentul  descris de propoziția „Un număr par apare cu fața în sus”. O variabilă aleatoare care ia valoarea 1 atunci când un număr par apare cu fața în sus și valoarea 0 în caz contrar este un indicator al evenimentului
descris de propoziția „Un număr par apare cu fața în sus”. O variabilă aleatoare care ia valoarea 1 atunci când un număr par apare cu fața în sus și valoarea 0 în caz contrar este un indicator al evenimentului  . Definiția cazuistică a acestui indicator este
. Definiția cazuistică a acestui indicator este
Din definiția de mai sus, se poate observa cu ușurință că  este o variabilă aleatoare discretă cu suport
este o variabilă aleatoare discretă cu suport  și funcție de masă de probabilitate
și funcție de masă de probabilitate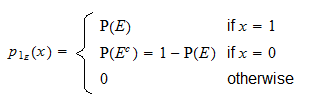
Proprietăți
Funcțiile indicatoare se bucură de următoarele proprietăți.
Putere
Puterea  -a a
-a a  este egală cu
este egală cu  :
: pentru că
pentru că  poate fi fie
poate fi fie  , fie
, fie  și
și
Valoarea așteptată
Valoarea așteptată a lui  este egală cu
este egală cu  :
: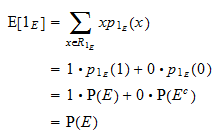
Varianța
Varianța lui  este egală cu
este egală cu  . Mulțumită formulei uzuale a varianței și proprietății puterilor de mai sus, obținem
. Mulțumită formulei uzuale a varianței și proprietății puterilor de mai sus, obținem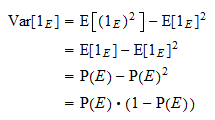
Intersecții
Dacă  și
și  sunt două evenimente, atunci
sunt două evenimente, atunci deoarece:
deoarece:
-
dacă
 , atunci
, atunci  și
și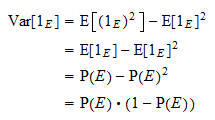
-
dacă
 , atunci
, atunci și
și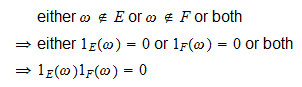
Indicatori ai evenimentelor cu probabilitate zero
Fie  un eveniment cu probabilitate zero și
un eveniment cu probabilitate zero și  o variabilă aleatoare integrabilă. Atunci,
o variabilă aleatoare integrabilă. Atunci, În timp ce o demonstrație riguroasă a acestui fapt depășește scopul acestei expuneri introductive, această proprietate ar trebui să fie intuitivă. Variabila aleatoare
În timp ce o demonstrație riguroasă a acestui fapt depășește scopul acestei expuneri introductive, această proprietate ar trebui să fie intuitivă. Variabila aleatoare  este egală cu zero pentru toate punctele de eșantionare
este egală cu zero pentru toate punctele de eșantionare  cu excepția, eventual, a punctelor
cu excepția, eventual, a punctelor  . Valoarea așteptată este o medie ponderată a valorilor pe care le poate lua
. Valoarea așteptată este o medie ponderată a valorilor pe care le poate lua  , unde fiecare valoare este ponderată cu probabilitatea sa respectivă. Valorile diferite de zero pe care le poate lua
, unde fiecare valoare este ponderată cu probabilitatea sa respectivă. Valorile diferite de zero pe care le poate lua  sunt ponderate cu probabilități zero, deci
sunt ponderate cu probabilități zero, deci  trebuie să fie zero.
trebuie să fie zero.
Exerciții rezolvate
Mai jos găsiți câteva exerciții cu rezolvarea explicată.
Exercițiu 1
Se consideră o variabilă aleatoare  și o altă variabilă aleatoare
și o altă variabilă aleatoare  definită ca funcție de
definită ca funcție de  .
.
Exprimați  folosind funcțiile indicatoare ale evenimentelor
folosind funcțiile indicatoare ale evenimentelor  și
și  .
.
Denotați prin  indicatorul evenimentului
indicatorul evenimentului  și notați prin
și notați prin  indicatorul evenimentului
indicatorul evenimentului  . Putem scrie
. Putem scrie  ca
ca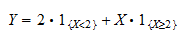
Exercițiu 2
Fie  o variabilă aleatoare pozitivă, adică o variabilă aleatoare care poate lua numai valori pozitive. Fie
o variabilă aleatoare pozitivă, adică o variabilă aleatoare care poate lua numai valori pozitive. Fie  o constantă. Să se demonstreze că
o constantă. Să se demonstreze că  unde
unde  este indicatorul evenimentului
este indicatorul evenimentului  .
.
În primul rând observați că suma indicatorilor  și
și  este întotdeauna egală cu
este întotdeauna egală cu  :
: În consecință, putem scrie
În consecință, putem scrie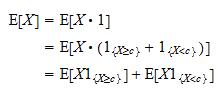 Acum, observați că
Acum, observați că  este o variabilă aleatoare pozitivă și că valoarea așteptată a unei variabile aleatoare pozitive este pozitivă:
este o variabilă aleatoare pozitivă și că valoarea așteptată a unei variabile aleatoare pozitive este pozitivă: Atunci,
Atunci,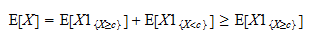
Exercițiu 3
Fie  un eveniment și să notăm funcția sa indicatoare prin
un eveniment și să notăm funcția sa indicatoare prin  . Fie
. Fie  complementul lui
complementul lui  și să se noteze funcția sa indicatoare prin
și să se noteze funcția sa indicatoare prin  . Se poate exprima
. Se poate exprima  ca funcție a lui
ca funcție a lui  ?
?
Suma celor doi indicatori este întotdeauna egală cu  :
: De aceea,
De aceea,
Cum se citează
Citează ca:
Taboga, Marco (2017). „Funcții indicatoare”, Lectures on probability theory and mathematical statistics, ediția a treia. Kindle Direct Publishing. Apendice online. https://www.statlect.com/fundamentals-of-probability/indicator-functions.