Ce este forma de interceptare a pantei

Forma de interceptare a pantei este una dintre cele trei forme pe care le putem folosi pentru a exprima o linie dreaptă. Celelalte forme se numesc forma punctului de pantă și forma standard, dar în această secțiune vom folosi în principal forma pantei de interceptare a pantei. Folosind forma de interceptare a pantei, exprimăm ecuația unei drepte ca fiind:

y=mx+by = mx + by=mx+b

Poate că știți că xxx și yyy sunt coordonatele unui punct pe un grafic, dar ce sunt mmm și bbb?

Ce este b în y=mx+b?

Litera b este un număr care reprezintă momentul în care dreapta atinge axa y. Ne referim, de asemenea, la aceasta ca fiind „intersecția y”. De exemplu, haideți să desenăm o dreaptă pe planul de coordonate.

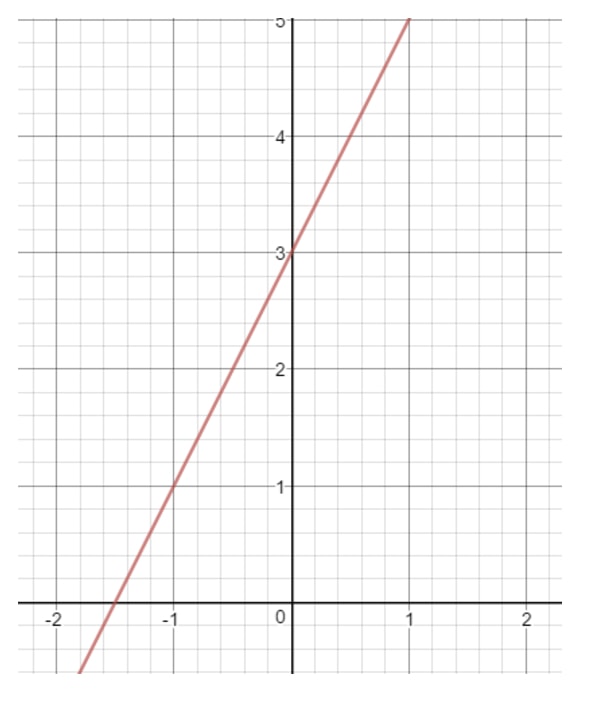
Dacă ar fi să ne uităm cu atenție la axa y, dreapta atinge axa y într-un anumit loc. Unde se află acel loc? Acela ar fi numărul 3, deoarece acolo se intersectează axa y și linia dreaptă. Acest lucru înseamnă că putem concluziona că b = 3.

Ce este m în forma panta interceptării?

Litera m este un număr care reprezintă panta dreptei. Unii oameni se referă la pantă ca fiind creșterea peste curbă. Reamintim că, dacă avem două puncte, atunci suntem capabili să găsim panta celor două puncte folosind formula pantei

m=riserun=y2-y1x2-x1m = \frac{rise}{run} = \frac{y_{2} – y_{1}}}{x_{2} – x_{1}}}m=runrise=x2-x1y2-y1

Aceeași idee funcționează și aici. Dacă luăm două puncte oarecare pe o dreaptă, atunci putem afla panta dreptei folosind formula de mai sus! De exemplu, să folosim această dreaptă.

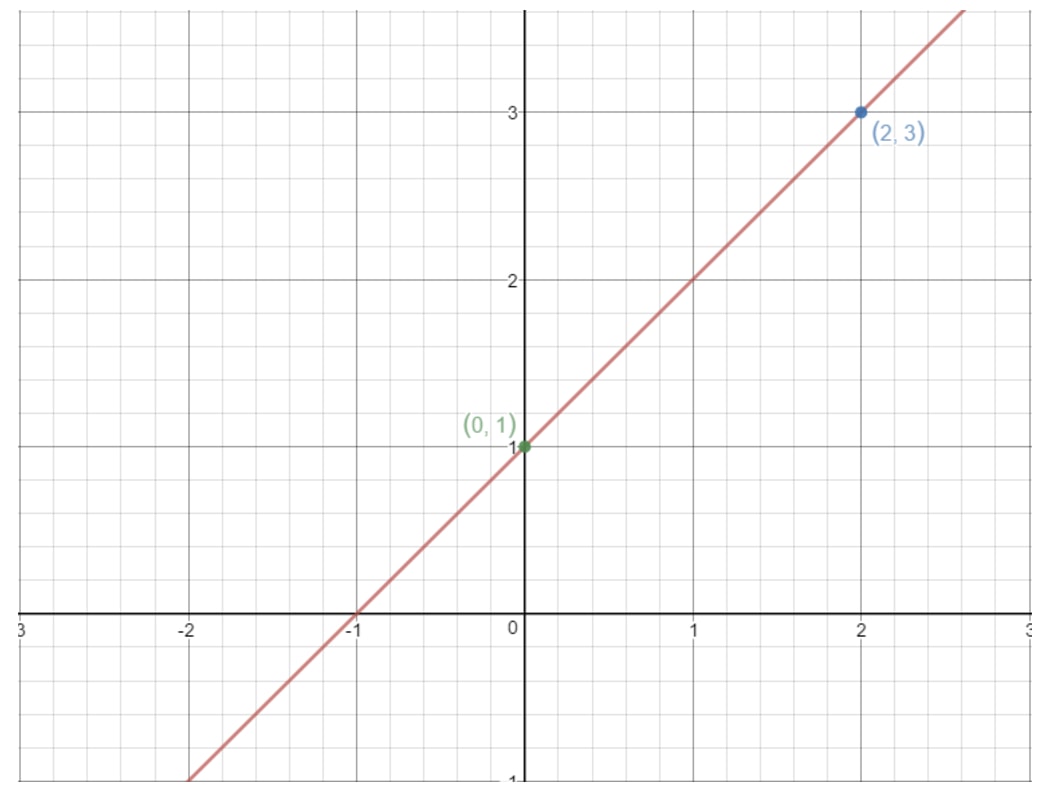
Observați că punctele (2, 3) și (0, 1) sunt pe acest grafic. Deci, de ce să nu folosim aceste două puncte pentru a găsi panta dreptei? Folosind formula, am obține:

m=y2-y1x2-x1-x1=1-30-2m = \frac{y_{2} – y_{1}}}{x_{2} – x_{1}}} = \frac{1 – 3}{0 – 2}m=x2-x1y2-y1=0-21-3=-2-2-2= \frac{-2}{-2}=-2-2-2=1= 1=1

Aceasta înseamnă că panta acestei drepte este 111!

Ceea ce este special la pante este că putem folosi oricare două puncte de pe dreaptă pentru a o găsi. Așadar, dacă ați lua două puncte diferite de pe această dreaptă, tot ați obține că panta este 111.

Cum să scrieți o ecuație în forma panta interceptării pantei?

Poate că știți cum arată forma panta interceptării pantei, dar jumătate din timp vi se vor da ecuații care nu sunt în această formă. Așadar, este de datoria voastră să le transformați în forma panta-intercepție. Cum facem acest lucru? Scopul este de a izola întotdeauna termenul yyy. De exemplu, să spunem că vi se dă ecuația

6x+4+2y=06x + 4 + 2y = 06x+4+2y=0

Pentru a izola yyy, mutăm 6x+46x + 46x+4 în partea dreaptă a ecuației

2y=-6x-42y = -6x – 42y=-6x-4

Acum 222 este în calea lui yyy, așa că vom scăpa de el prin împărțirea ambelor părți ale ecuației la 222.

2y2=-6x-42\frac{2y}{2}2} = \frac{-6x – 4}{2}22y=2-6x-4y=-6×2-42y = -\frac{6x}{2}. – \frac{4}{2}y=-26x-24y=-3x-2y = -3x – 2y=-3x-2

Din moment ce yyy este izolat, se poate vedea că este sub forma panta-intercepție y=mx+by = mx + by=mx+b unde m=-3m = -3m=-3, iar b=-2b = -2b=-2.

Acum că știm foarte bine intercepția și panta y, de ce să nu ne uităm la întrebări specifice despre găsirea lor!

Cum se găsește interceptarea lui y?

Întrebarea 1: Folosind ecuația liniară y=12x+5y = \frac{1}{2} x + 5y=21x+5, găsiți interceptarea lui y.

Observați aici că ecuația este deja în forma panta-interceptare y=mx+by = mx + by=mx+b. Trebuie doar să aflăm ce este bbb. Vedem că b=5b = 5b=5, deci interceptarea y este 555.

Să facem o întrebare puțin mai dificilă.

Întrebarea 2: Determinați interceptarea y a ecuației 2x-4y=82x – 4y = 82x-4y=8

Acum această ecuație liniară nu este în forma pantă-interceptare, deci trebuie să o schimbăm mai întâi în această formă. Scopul nostru este să izolăm yyy în această ecuație.

Vezi că, dacă mutăm 2x2x2x în partea dreaptă a ecuației, vom avea:

-4y=8-2x-4y = 8 – 2x-4y=8-2x

Acum, împărțind ambele părți la -4-4-4, vom obține:

-4y=8-2y=8-2x

Acum, împărțind ambele părți la -4-4-4, vom obține:

-4y-4=8-2x-4\frac{-4y}{-4} = \frac{8 – 2x}{-4}-4-4-4y=-48-2xy=8-4-2x-4y = \frac{8}{-4}{-4} – \frac{2x}{-4}y=-48–42xy=-2+12xy = -2 + \frac{1}{2}xy=-2+21x

Acum, schimbând pozițiile celor doi termeni obținem:

y=12x-2y = \frac{1}{2}x – 2y=21x-2

Întrebare 3: Determinați intercepția y a lui 4y-8=04y – 8 = 04y-8-8=0.

Acest lucru poate părea puțin ciudat, deoarece nu există un termen xxx, dar scopul nostru rămâne același. Vom izola yyy.

Mutarea lui -8-8-8-8 în partea dreaptă a ecuației ne dă:

4y=84y = 84y=8

Divizând ambele părți ale ecuației cu 444 ne dă

4y4=84\frac{4y}{4} = \frac{8}{4}44y=48y=2y = 2y=2

Acum s-ar putea să nu pară așa, dar ecuația este în forma panta-intercept. Doar că m=0m = 0m=0, astfel încât întregul termen mxmxmxmx a dispărut. Doar rescrieți ecuația sub forma

y=0m+2y = 0m + 2y=0m+2

Din observație, vă puteți da seama că b=2b = 2b=2, și deci intersecția y este 222. Să mai facem încă o întrebare.

Întrebarea 4: Determinați (dacă este posibil) interceptarea y a lui 5x-15=05x – 15 = 05x-15=0.

Aceasta este interesantă pentru că ecuația nu are un termen yyy. Deci, cum ar trebui să o punem sub forma de interceptare a pantei? Ei bine, singurul lucru pe care îl putem face acum este să izolăm pentru xxx, așa că hai să încercăm asta deocamdată.

Mutând 151515 în partea dreaptă a ecuației avem:

5x=155x = 155x=15

Divizând ambele părți ale ecuației rezultă:

5x=155x = 155x=15

Divizând ambele părți ale ecuației rezultă:

5×5=155\frac{5x}{5} = \frac{15}{5}55x=515x=3x = 3x=3

Acum vom desena acest lucru pe un grafic. Observați că în această ecuație, xxx este forțat să fie 333 și nu poate fi altceva. Cu toate acestea, nu se spune nimic despre yyy, așa că yyy poate fi orice dorește. Dacă ar fi să scriem un tabel de valori, obținem:

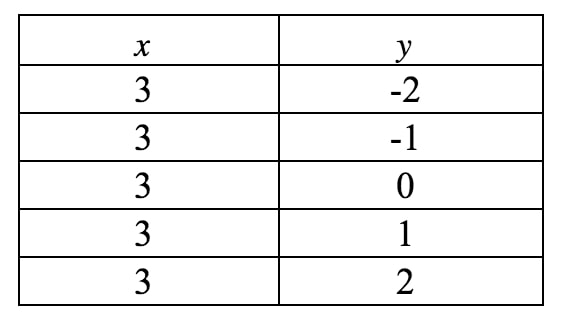
Dacă vom trasa aceste puncte pe un plan de coordonate și vom trasa dreapta, vom avea:

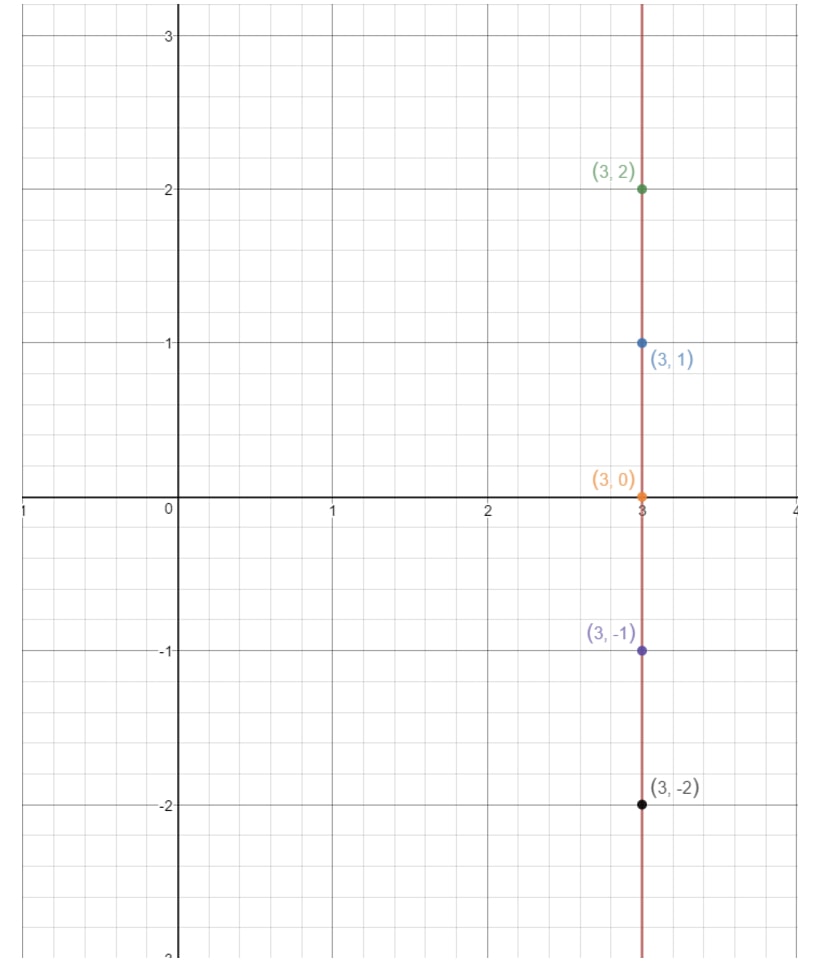
Observați cum linia nu atinge niciodată axa y. Acest lucru înseamnă că ecuația nu are o interceptare y. Acum că am acoperit toate cazurile de găsire a coordonatei y, să ne uităm la întrebările care ne cer să găsim panta!

Cum să găsim panta unei ecuații?

Întrebare 5: Găsiți panta ecuației y=32x+1y = \frac{3}{2}x + 1y=23x+1

Întrebare 6: Determinați panta ecuației liniare 6x-6y=06x – 6y = 06x-6y=0

După cum vedeți, ecuația nu este sub forma panta interceptării pantei, așa că trebuie să o convertim mai întâi în această formă. Scopul nostru este să izolăm yyy.

Mutând 6x6x6x în partea dreaptă a ecuației rezultă:

-6y=-6x-6y = -6x-6y=-6x

Divizând ambele părți cu -6-6-6-6 rezultă:

-6y=-6x-6y = -6x-6y=-6x

Divizând ambele părți cu -6-6-6 rezultă:

-6y-6=-6x-6\frac{-6y}{-6} = \frac{-6x}{-6}-6-6y=-6-6-6xy=xy = xy=x

Observați că aceasta este, de fapt, sub forma de interceptare a pantei y=mx+by = mx + by=mx+b. Doar că interceptul y bbb în acest caz este 000, iar xxx este același cu 1x1x1x. Deci putem rescrie ecuația astfel:

y=1x+0y = 1x + 0y=1x+0

Acum, prin observare, vedem că m=1m = 1m=1. Deoarece mmm este panta, atunci panta trebuie să fie 111. Să facem una puțin mai dificilă

Întrebarea 7: Determinați panta lui 2y-4=02y – 4 = 02y-4-4=0

Din nou, aceasta este puțin ciudată pentru că nu avem un termen xxx. Cu toate acestea, obiectivul nostru de a izola yyy rămâne același.

Mutând -4-4-4 în partea dreaptă a ecuației avem:

2y=42y = 42y=4

Divizând ambele părți ale ecuației cu 222 obținem:

2y=42y = 42y=4

:

2y2=42\frac{2y}{2} = \frac{4}{2}22y=24y=2y = 2y=2

Vezi aici că acum este sub forma panta-intercept, doar că termenul mxmxmx este ascuns deoarece m=0m = 0m=0. Deci putem rescrie ecuația noastră ca:

y=0x+2y = 0x + 2y=0x+2

Din moment ce m=0m = 0m=0, atunci avem o pantă zero. Dacă vă întrebați cum arată o dreaptă cu panta 000, atunci iată un grafic pe care să îl vedeți.

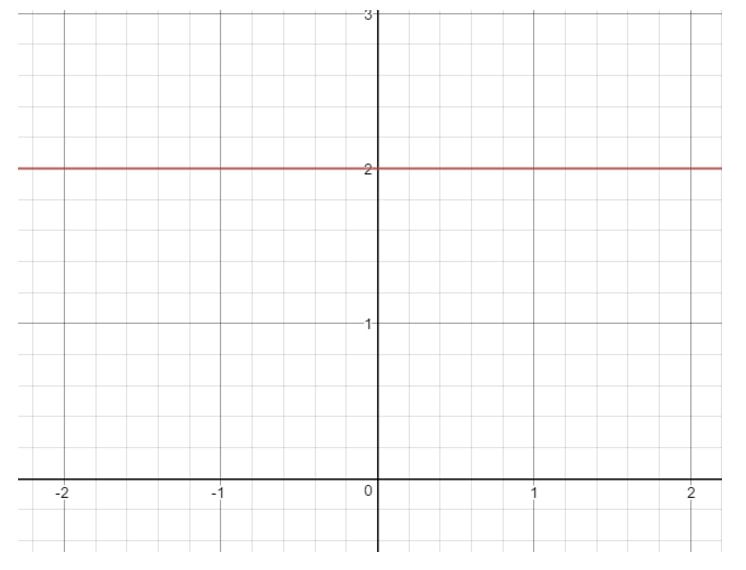
Întrebare 8: Găsiți (dacă este posibil) panta ecuației liniare 16-4x=016 – 4x = 016-4x=0

În acest caz, yyy nu poate fi izolat pentru că nu există un termen yyy. Așadar, singurul lucru pe care îl putem face este să izolăm xxx.

Mutarea lui 161616 în partea dreaptă a ecuației dă:

-4x=-16-4x = -16-4x=-16

Divizând ambele părți cu -4-4-4, obținem:

-4x-4=-16-4-4\frac{-4x}{-4} = \frac{-16}{-4}-4-4-4x=-4-16x=4x = 4x=4

Aceasta nu este încă în forma panta-intercept, astfel încât singura noastră speranță de a obține panta este de a trasa un grafic al acestei drepte. Din nou, vedem că xxx este întotdeauna forțat să fie 444, dar yyy poate fi orice dorește, deoarece nu există un termen yyy. Dacă ar fi să scriem un tabel de valori, obținem:

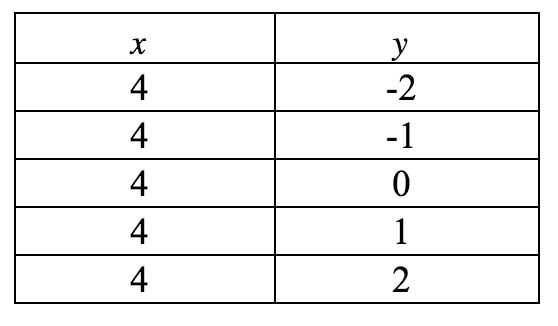
Dacă vom reprezenta aceste puncte pe un plan de coordonate și vom trasa dreapta, vom avea

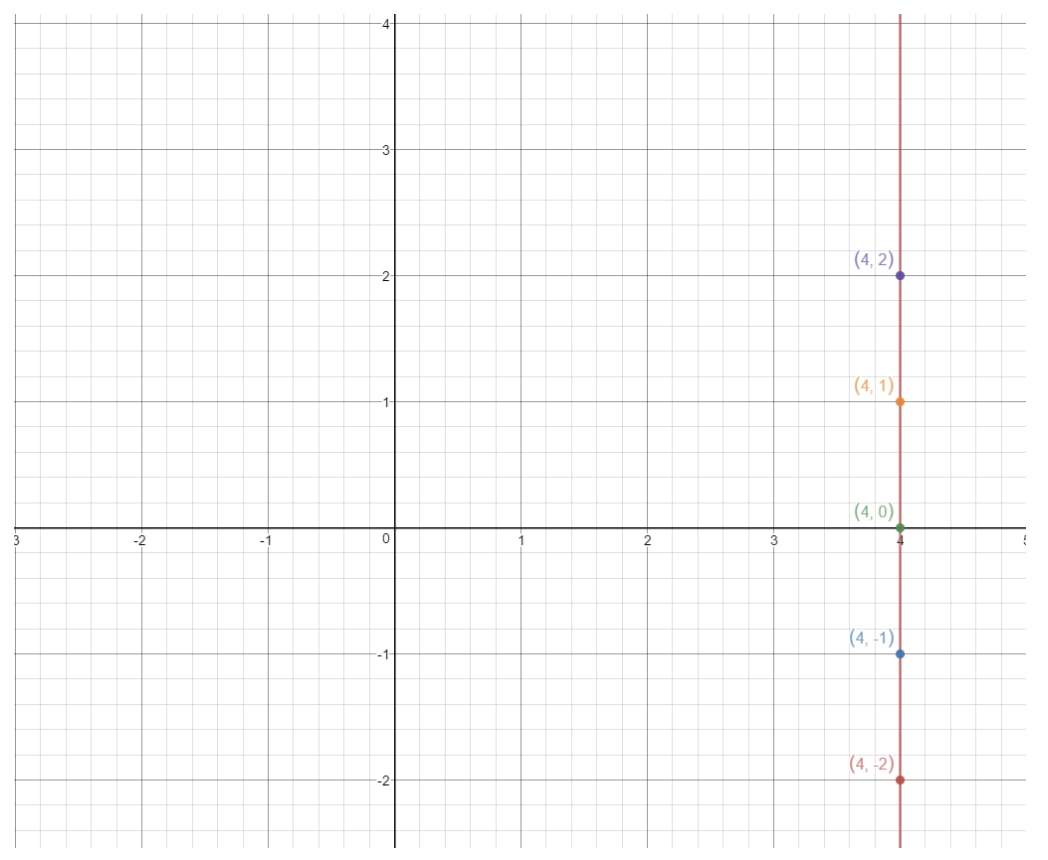
Aceasta este o dreaptă verticală. Deci, care este panta unei drepte verticale? Haideți să încercăm să ne dăm seama de acest lucru, găsind creșterea și cursa. Observați cum această linie crește întotdeauna la infinit, dar nu există nici un fel de cursă. Deci, asta înseamnă că alergarea este 000. Deci, dacă calculăm panta, atunci vom obține:

m=riserun=rise0=undefinedm = \frac{rise}{run} = \frac{rise}{0} = undefinedm=runrise=0rise=undefined

Nu putem împărți la 000, deci avem de fapt o pantă nedefinită.

Ce este o pantă nedefinită?

O pantă nedefinită este o pantă care merge direct în sus pe grafic. După cum se vede în graficul de mai sus, panta crește la infinit și nu are cursă. Ca urmare, obținem o pantă nedefinită deoarece nu putem împărți la 000.

În general, obținem întotdeauna o pantă nedefinită ori de câte ori obținem o dreaptă verticală!

Să ne uităm la alte întrebări unice!

Găsirea ecuației dintr-un punct

Întrebarea 9: Un punct (2, 6) trece printr-o ecuație de y=-5x+by = -5x + by=-5x+b. Găsiți „bbb”.

6=-5(2)+b6 = -5(2) + b6=-5(2)+b

Izolvând și rezolvând pentru bbb se obține:

6=-10+b6 = -10 + b6=-10+bb=16b = 16b=16

Amintiți-vă că bbb este cunoscută și sub numele de intersecția y, deci și intercepția y este 161616!

Cercetarea pantei din două puncte

Întrebarea 10: Date fiind două puncte (6, 1) și (-10, 9), găsiți panta dreptei.

Reamintim că pentru a găsi panta dreptei, folosim ecuația pantei

m=y2-y1x2-x1m = \frac{y_{2} – y_{1}}}{x_{2} – x_{1}}}m=x2-x1y2-y1

În consecință, folosind această formulă obținem:

m=9-1-10-6=8-16m = \frac{9 – 1}{-10 – 6} = \frac{8}{-16}m=-10-69-1=-168

=1-2= \frac{1}{-2}=-21

Și dacă în schimb trebuie să găsim întreaga ecuație a unei drepte?

Ecuația unei drepte date două puncte

Întrebarea 11: Date două puncte (-6, 1) și (2, 6), găsiți ecuația sub forma pantei interceptării.

În principiu, încercăm să găsim ecuația sub forma y=mx+by = mx + by=mx+b. Pentru a face acest lucru, trebuie să căutăm mmm și bbb.

Reamintim că, pentru a găsi mmm, folosim ecuația pantei

m=y2-y1x2-x1m = \frac{y_{2} – y_{1}}}{x_{2} – x_{1}}}m=x2-x1y2-y1

În consecință, folosind această formulă obținem:

m=6-12-(-6)=58m = \frac{6 – 1}{2 – (- -6)} = \frac{5}{8}m=2-(-6)6-1=8558\frac{5}{8}85

Acum avem ecuația

y=58x+by = \frac{5}{8}x + by=85x+b

Acum trebuie să căutăm bbb. Pentru a rezolva bbb, alegem oricare dintre punctele date și îl introducem în ecuație. Putem face acest lucru deoarece ambele puncte se află pe dreaptă, iar orice punct de pe dreaptă ar satisface ecuația. Să folosim punctul (2, 6). Vedeți că:

6=58(2)+b6 = \frac{5}{8}(2) + b6=85(2)+b

Isolând bbb rezultă:

6=108+b6 = \frac{10}{8} + b6=810+bb=6-108b = 6 – \frac{10}{8}b=6-810b=488-108b = \frac{48}{8} – \frac{10}{8}b=848-810b=388b = \frac{38}{8}b=838

Punând acest lucru în formă zecimală, obținem că b=4,75b = 4,75b=4,75. Prin urmare, ecuația noastră sub forma de interceptare a pantei este:

y=58x+4.75y = \frac{5}{8}x + 4.75y=85x+4.75

Ultimul lucru pe care trebuie să-l acoperim în această secțiune este găsirea domeniului și a intervalului unei drepte.

Cum găsim domeniul și intervalul?

Pentru a găsi domeniul unei drepte, ne punem practic această întrebare: ce poate fi xxx? Dacă xxx poate fi acele valori, atunci le adăugăm în domeniu.

Același lucru este valabil și pentru interval. Ce poate fi yyy? Dacă yyy pot fi acele valori, atunci le adăugăm în interval. Să dăm un exemplu.

Întrebarea 12: Găsiți domeniul și intervalul ecuației y=2x+1y = 2x + 1y=2x+1.

Observați că dacă desenăm graficul acestei drepte, atunci vom obține:

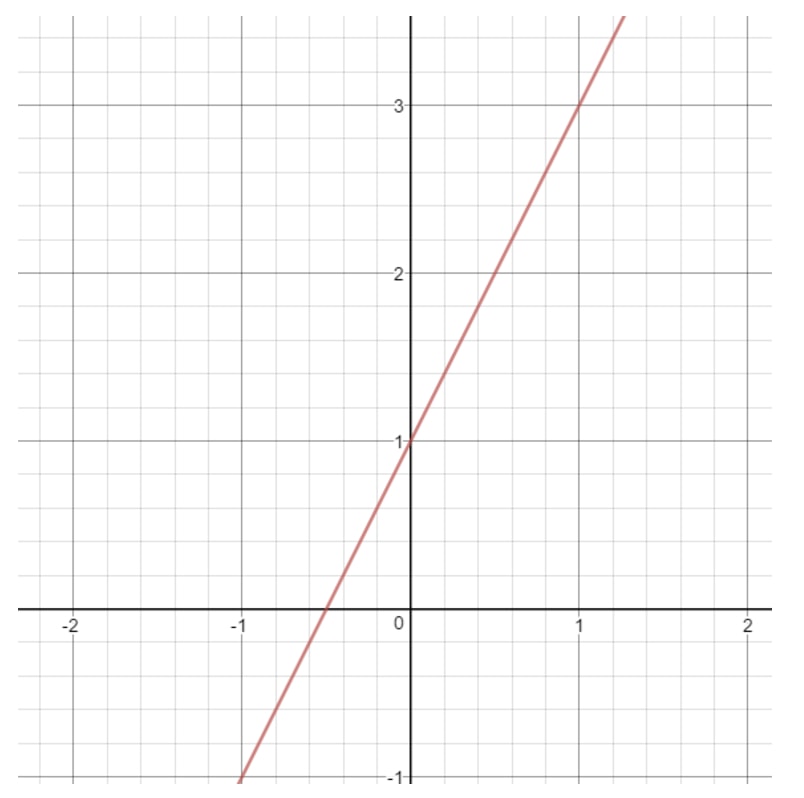
Ce poate fi xxx în această dreaptă? Observați că xxx poate fi orice, deoarece cu orice valoare xxx, putem obține un punct care se află pe dreaptă. Același lucru este valabil și pentru y. Putem oricând să alegem o valoare yyy care să ne dea un punct pe o dreaptă. Așadar, spunem că

Domeniu: {x∈\in∈R}Range: {y∈\in∈R}

unde R înseamnă „toate numerele reale”. Să facem una mai dificilă.

Întrebarea 13: Găsiți domeniul și intervalul ecuației y=-2y = -2y=-2.

Acum, dacă tragem această dreaptă pe un grafic, vom obține:

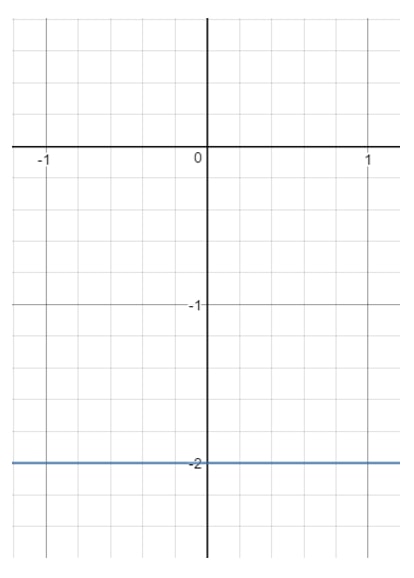
Observați că xxx poate fi orice, deoarece cu orice valoare xxx, putem obține un punct care se află pe dreaptă atâta timp cât y=-2y = -2y=-2. Totuși, uitați-vă la yyy. Observați că yyy este forțat la -2-2-2-2 și nu poate fi altceva. În momentul în care alegeți o altă valoare yyy (cum ar fi 111), atunci acel punct va fi în afara liniei. Deci, asta înseamnă că:

Domiciliu: {x ∈\in∈ R}Range: {y = -2}

Întrebarea 14: Găsiți domeniul și intervalul ecuației x=1x = 1x=1.

Acum, dacă desenăm această dreaptă pe un grafic, vom obține:

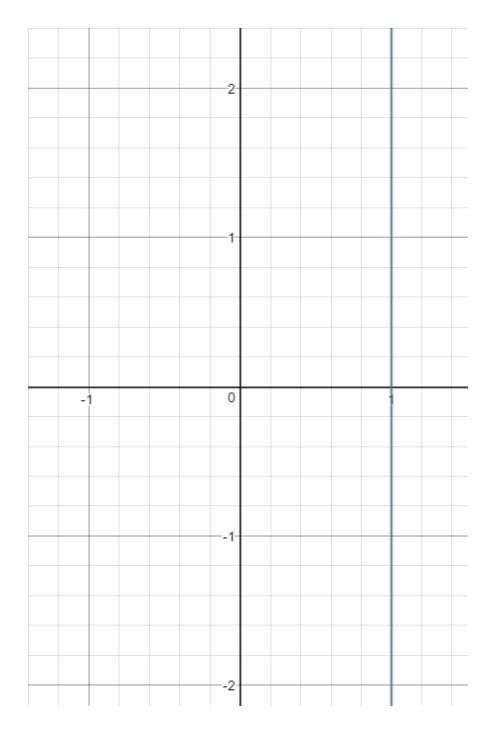
Vezi că xxx este forțat la 111 și nu poate fi altceva. În momentul în care alegeți o altă valoare xxx (cum ar fi 222), atunci acel punct va fi în afara liniei.Totuși, uitați-vă la yyy. Observați că yyy poate fi orice, deoarece cu orice valoare yyy, putem obține un punct care se află pe dreaptă atâta timp cât x=1x = 1x=1

Așa că asta înseamnă:

Domeniu: {x=1}Range: {y∈\in∈R}

Dacă ați avut o mulțime de probleme în trasarea graficelor pentru a obține domeniul și intervalul, vă recomand să folosiți acest calculator.

https://www.desmos.com/calculator/2rnqgoa6a4

Vă învață cum să reprezentați grafic o ecuație liniară. Tot ce trebuie să faceți este să introduceți valorile lui mmm și bbb. Apoi, acesta va trasa automat linia pentru tine! Acest lucru este util și atunci când încercați să găsiți forma de interceptare a pantei.

.