Zero este un număr care se situează exact între numerele pozitive și cele negative de pe linia numerelor. Zero este considerat un număr întreg, alături de numerele naturale pozitive (1, 2, 3, 3, 4…) și de numerele negative, (…-4,-3,-2,-1).

Zero este un număr special în cadrul numerelor întregi, deoarece este singurul număr întreg care nu este nici pozitiv, nici negativ. De asemenea, este singurul număr întreg care nu este nici număr prim și nici număr compus. Este considerat un număr par deoarece este divizibil cu 2 fără rest. Zero este elementul aditiv identitar în diferite sisteme de algebră, iar cifra „0” este folosită ca valoare de rezervă în sistemele de notație pozițională pentru reprezentarea numerelor.

Zero are multe proprietăți interesante care îl fac să fie de interes pentru matematicieni. Dacă adăugați sau scădeți zero din orice număr, numărul rămâne același Dacă înmulțițiți 0 cu orice număr, rezultatul este 0. Orice număr ridicat la puterea zero (a 0-a) este 1, deci 20=1 și 560=1. În algebra tradițională, împărțirea la 0 este nedefinită, deci niciun număr nu poate fi împărțit la 0. Numărul 0 este, de asemenea, un element al numerelor reale și al numerelor complexe.

Istoria numărului 0

De unde a apărut ideea de zero? În zilele noastre, ea ne pare intuitivă; zero este numărul care reprezintă o cantitate nulă – un nimic. Vedem zerouri peste tot în societate și, în mod natural, înțelegem ce înseamnă și cum pot fi manipulate matematic. Totuși, din punct de vedere istoric, conceptul de 0 a avut nevoie de ceva timp pentru a fi recunoscut în mod universal ca obiect al matematicii, iar mulți de-a lungul istoriei au susținut că numărul zero nu există sau că ideea de zero este un concept incoerent.

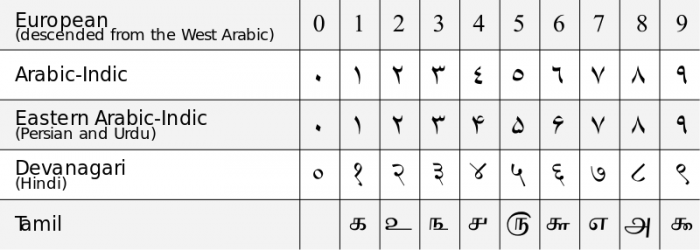
Multe societăți antice nu aveau un concept explicit al cantității zero sau o cifră specifică pe care să o folosească pentru reprezentarea sa. Egiptenii antici și babilonienii aveau amândoi o anumită idee despre o cantitate nulă și o nevoie de valori de rezervă în reprezentarea numerelor, dar nu au dezvoltat niciodată o cifră sau un concept distinct pentru a reprezenta acea cantitate sau valoare de rezervă. Sistemele de numerație ale vechilor egipteni erau în întregime picturale și nu aveau valori de poziționare, în timp ce babilonienii antici foloseau spații între numere pentru a reprezenta valori de poziționare.

Maiașii au avut un concept explicit de 0 și au avut o cifră distinctă pentru a reprezenta acest concept și pentru a-l folosi ca valoare de rezervă în sistemul lor calendaristic vigesimal (baza 20). În timp ce societățile mayașă, olmecă și alte societăți precolumbiene au fost printre primele din istorie care au avut o înțelegere explicită și sofisticată a numărului 0, aceste sisteme nu au continuat să influențeze societățile din Lumea Veche în Europa.

Grecii antici, pe de altă parte, au avut o relație complicată cu zero. Ei nu aveau un simbol pentru conceptul său sau pentru el ca valoare de rezervă, deoarece nu erau siguri că numărul 0 poate fi considerat un lucru cu adevărat existent. Cum, se întrebau ei, ar putea ceva (un număr) să nu fie nimic (zero)? Pentru greci, numerele naturale (1, 2, 3, 4,…) au fost derivate din înțelegerea noastră a obiectelor individuale discrete din lume. Aristotel însuși a susținut în mod faimos că 0 nu există, pe motiv că 0 reprezintă un vid sau un neant, iar un vid sau un neant veritabil nu poate exista.

Cinezii aveau o înțelegere a lui „0” ca cifră de rezervă pentru sistemele lor de numărare, dar ei nu considerau că cifra „0” reprezintă vreun număr distinct, ci doar un simbol util. Înțelegerea comună a lui „0” ca număr distinct și ca cifră pentru sistemele de notație pozițională a venit din India în secolul al VI-lea d.Hr. Matematicienii indieni de la acea vreme au dezvoltat primele tipuri de sisteme de notație zecimală (baza 10) care încorporau cifra 0 ca cifră distinctă și aveau o înțelegere a proprietăților matematice unice ale lui zero. În secolul al XI-lea d.Hr., ideea de zero s-a răspândit în Europa de Vest prin influența matematicienilor islamici care trăiau în Spania sub califatul Umayyad și a fost creat sistemul de notație zecimală cu cifre arabe din zilele noastre. Prima utilizare a cuvântului englezesc „zero” datează din 1589.

Proprietăți matematice ale lui zero

Numărul zero joacă un rol integral în aproape toate domeniile matematicii. Zero este cel mai mic număr întreg non-negativ și nu are un număr natural care să îl urmeze. Deoarece 0 este un număr întreg, el este, de asemenea, un număr rațional, un număr real și un număr complex. În matematică, 0 este considerat o cantitate care corespunde unei cantități nule. Se poate spune că zero este „cantitatea” pe care o posedă un ansamblu care nu are membri.

În algebră

În algebra elementară, zero este adesea exprimat ca fiind situat în centrul dreptei numerice. Numărul 0 este considerat un număr par, deoarece este un multiplu întreg al numărului 2 (2×0=0). 0 nu este un număr prim, deoarece are o cantitate infinită de factori, și nu este un număr compus, deoarece niciun produs a două numere prime nu este egal cu numărul 0.

În raport cu cei 4 operatori aritmetici principali (+, -, ×, ÷) și cu operația cu exponentul, numărul 0 se comportă după următoarele reguli:

• Addenda: x+0=0+x=x. Zero este considerat elementul aditiv identitar, deoarece orice număr plus sau minus zero este egal cu acel număr
• Substracție: x-0=x și 0-x=-x
• Multiplicare: x⋅0=0⋅x=0. Orice număr înmulțit cu 0 este de asemenea egal cu 0.
• Diviziune: 0/x=0, cu excepția cazului în care x=0. x/0 este o cantitate nedefinită din punct de vedere matematic, deoarece 0 nu are un invers multiplicativ (niciun număr înmulțit cu 0 nu dă 1).
• Exponenți: x0=1, cu excepția cazului în care x=0. A existat o lungă dezbatere cu privire la faptul dacă 00 este nedefinit sau o expresie bine formată. Pentru orice x pozitiv, 0x=0.

În expresii care implică limite, cantitatea 0/0 poate apărea în contextul demonstrării limitelor funcțiilor raționale precum f(x)/g(x). În aceste cazuri, 0/0 nu este nedefinită, ci reprezintă o formă nedeterminată. Acest lucru nu înseamnă că limita este nedefinită, ci că ea trebuie calculată printr-o altă metodă, cum ar fi găsirea derivatelor. Există unele modele algebrice în care împărțirea la zero dă o mărime definită, cum ar fi linia reală extinsă proiectiv sau sfera lui Riemann.

În teoria seturilor

În teoria seturilor, numărul 0 corespunde cardinalității „setului gol” sau „setului nul” (reprezentat în mod obișnuit prin {} sau {∅}. Cardinalitatea unui set este cantitatea de elemente din acel set dacă nu se are nici o portocală, atunci se are un set de 0 portocale (un set gol de portocale).

Zero este adesea folosit ca punct de plecare în teoria seturilor pentru a construi restul numerelor naturale. Aceste construcții von Neumman, numite după renumitul polimat John von Neumann construiește numerele naturale prin definirea 0={} și definește o funcție succesoare S(a) = a ∪ {a}. Totalitatea numerelor naturale poate fi construită din aplicațiile recursive ale funcției succesoare începând cu setul gol:

0 = {}

1 = 0 ∪ {0} = {0} = {{}}

2 = 1 ∪ {1} = {0,1} = {{}, {{}}}

3 = 2 ∪ {2} = {0, 1, 2} = {{}, {{}}, {{}, {{}, {{}}}}

și așa mai departe. Urmând acest model, se poate construi întregul set infinit al numerelor naturale. În acest fel, se poate spune că fiecărui număr natural îi corespunde ansamblul care conține toate numerele naturale dinaintea lui.

În fizică

În contextul efectuării măsurătorilor cantitative în fizică, 0 este considerat a fi linia de bază de la care se fac toate celelalte măsurători de unități. Foarte adesea, linia de bază 0 corespunde unei variabile semnificative din punct de vedere fizic, care se distinge în mod natural de toate celelalte mărimi de măsurare.

De exemplu, în scara Kelvin, o temperatură de 0 K corespunde la 0 absolut – cea mai rece temperatură care este fizic posibilă. În scara de temperatură Celsius, 0 °C este definit ca fiind punctul de îngheț al apei la presiuni atmosferice. În contextul dinamicii și al electromagnetismului, o valoare de 0 este dată poziției în care un sistem are cea mai mică cantitate posibilă de energie potențială. De exemplu, stării fundamentale a unui atom, cel mai mic nivel de energie posibil pentru electronii din atom, i se atribuie adesea valoarea 0.

De asemenea, în contextul cinematicii, cadrul de referință din care se fac observații ale mișcării este definit ca având un punct central așezat pe originea axei de coordonate în punctul (0, 0). În cazul mărimilor conservate, cum ar fi masa-energie, momentul și momentul unghiular, valoarea totală a modificării mărimilor conservate într-un sistem izolat este întotdeauna egală cu 0.

În informatică

Computerele stochează informații sub formă de secvențe de biți de 1 și 0, lungi de biți. În această reprezentare binară, 0 corespunde unei poziții „oprit” și este în contrast cu poziția „pornit” desemnată prin 1. O valoare de 0 pe un circuit electric înseamnă că circuitul este oprit și nu are niciun flux electric. În mod similar, multe logici computaționale definesc „0” ca fiind caracterul care reprezintă o valoare de adevăr falsă.

În bazele de date informatice, elementele unei matrice sunt numărate folosind un sistem de numărare bazat pe zero. Aceasta înseamnă că, pentru un set cu n elemente, elementele au indici care încep cu 0. Astfel, un element cu un număr de index 0 este de fapt primul element din serie, iar un număr de index 1 corespunde celui de-al doilea element și așa mai departe. În general, al n-lea termen al unui set are un număr de index corespunzător lui n-1. Acest sistem de numărare poate provoca confuzie pentru programatorii începători care sunt obișnuiți să atribuie intuitiv valori de index care încep cu 1.

.