În timp ce lumina se reflectă sau se transmite dintr-o structură materială, se produce o modificare a polarizării. Elipsometria măsoară acest răspuns care depinde de proprietățile optice și de grosimea materialelor individuale. Elipsometria este utilizată în principal pentru a determina constantele optice și grosimea peliculei, dar și pentru a caracteriza compoziția, cristalinitatea, rugozitatea, concentrația de dopaj și alte proprietăți ale materialului asociate cu o modificare a răspunsului optic.
Amplasamentele sunt cercetarea de bază în științele fizice, soluții de stocare a semiconductorilor și a datelor, ecrane plate, comunicații, biosenzori și industrii de acoperire optică. Elipsometria are, de asemenea, flexibilitatea de a măsura majoritatea tipurilor de materiale: dielectrici, semiconductori, metale, supraconductori, materiale organice, acoperiri biologice și materiale compozite.
Definirea luminii polarizate
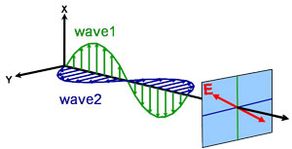
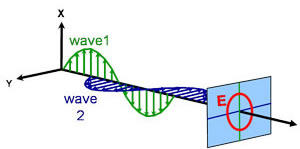
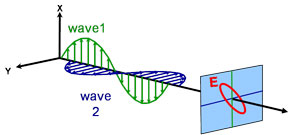
Lumina poate fi descrisă ca o undă electromagnetică ce călătorește prin spațiu. Modul în care se comportă câmpul unei unde electromagnetice în raport cu spațiul și timpul se numește polarizare. Lumina este considerată a fi nepolarizată atunci când orientarea și faza ei sunt total arbitrare. Cu toate acestea, elipsometria măsoară lumina polarizată – un câmp electric care urmează o traiectorie specifică și are o formă distinctă în orice punct dat. O undă electromagnetică care se deplasează în direcția z poate fi descrisă prin componentele sale x și y, deoarece câmpul său electric este întotdeauna ortogonal la direcția de propagare. Atunci când două unde luminoase ortogonale sunt în fază, lumina rezultată este polarizată liniar. Orientarea sa este determinată de amplitudinile relative. Lumina este considerată polarizată circular dacă undele ortogonale sunt defazate cu 90° și au aceeași amplitudine. Cea mai frecventă polarizare este cea eliptică și combină unde ortogonale de amplitudine și fază arbitrare. De aici își trage numele elipsometria.
Diferite tipuri de polarizare:
Liniară
Circulară
Eliptică
Proprietăți optice
Proprietățile optice care determină modul în care lumina interacționează cu un material sunt descrise de două valori. Acestea sunt reprezentate, în general, sub forma unui număr complex. Indicele de refracție complex (ñ) este format din indicele (n) și un coeficient de extincție (k):
![]()
Proprietățile optice pot fi, de asemenea, reprezentate ca o funcție dielectrică complexă:
![]()
cu următoarea relație între convenții:
![]()
Indicele descrie viteza de fază a luminii atunci când se deplasează într-un material în comparație cu viteza luminii atunci când se deplasează în vid, c:
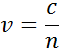
Când intră într-un material cu un indice mai mare, lumina încetinește. Deoarece frecvența undelor luminoase nu se modifică, lungimea de undă se scurtează. Pierderea de energie a undelor în material este descrisă de coeficientul de extincție, care este legat de coeficientul de absorbție după cum urmează:
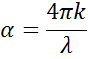
Conform legii lui Beer, lumina își pierde din intensitate într-un material absorbant. Coeficientul de extincție demonstrează cât de repede dispare lumina într-un material.
![]()
Figura 4 arată o undă luminoasă care călătorește prin două materiale diferite, cu proprietăți diferite, înainte de a se întoarce în mediul ambiant.
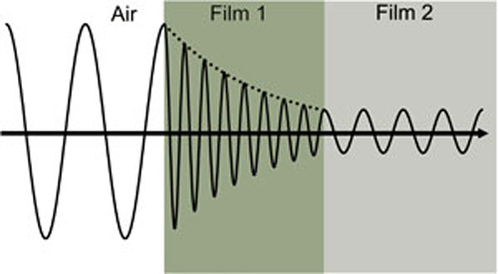
Figura 4: Unda luminoasă care călătorește din aer în pelicula absorbantă 1 și apoi în pelicula transparentă 2. Viteza de fază și lungimea de undă se modifică în ambele materiale în funcție de indicele de refracție (Filmul 1: n=4, Filmul 2: n=2).
Lungimea de undă determină constantele optice. Figura 5 prezintă constantele optice pentru TiO2 de la UV la IR. Din cauza proceselor diferite care extrag energie din unda luminoasă, absorbția (k>0) are loc atât în UV, cât și în IR. Absorbția în IR este cauzată, de obicei, de vibrația moleculară sau a fononilor sau a purtătorilor liberi. Absorbția în UV are loc, în general, din cauza tranzițiilor electronice, unde energia luminoasă excită electronii în stări ridicate. Figura 5 arată că constantele optice ipotetice sau reale nu sunt independente, ci legate matematic prin relațiile Kramers-Kronig.
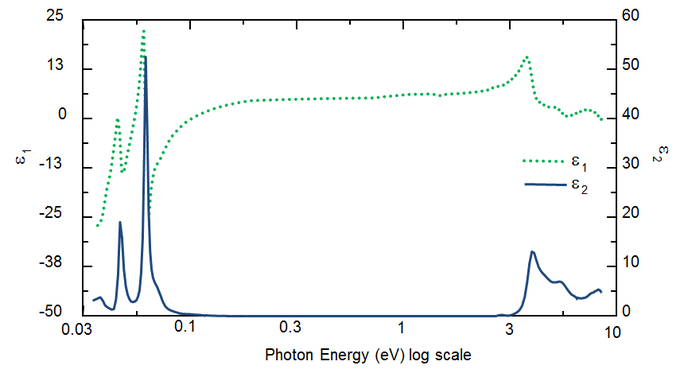
Figura 5: Funcția dielectrică complexă pentru filmul de TiO2 cu lungimi de undă de la IR (eV mici) la UV (eV mari).
Interacțiunea dintre lumină și materiale
Când lumina interacționează cu un material, aceasta duce la condiții limită la interfață. În timpul acesteia, ecuațiile lui Maxwell trebuie să rămână întotdeauna satisfăcute. Figura de mai jos arată modul în care lumina incidentă se reflectă și se refractă la interfață. Unghiul dintre raza incidentă și normala probei (θi) va fi egal cu unghiul reflectat (θr). Lumina care intră într-un material este refractată la un unghi θt dat de:
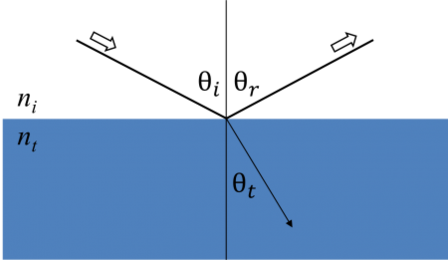
Figura 6: Lumina se reflectă și se refractă conform legii lui Snell.
La fiecare interfață o parte din lumină este reflectată în timp ce restul se transmite la unghiul refractat. În funcție de condițiile la limită, se aplică soluții diferite pentru câmpuri electrice paralele și perpendiculare pe suprafața probei. Astfel, lumina poate fi separată în componente ortogonale în raport cu planul de incidență (p- și s-polarizate). Ambele componente pot fi calculate separat. Iată cum a descris Fresnel cantitatea de lumină reflectată și transmisă la o interfață între materiale:
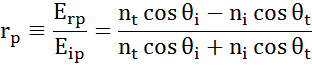
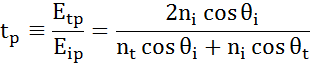
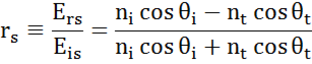
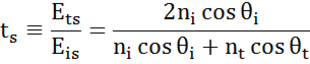
Interfețele multiple cu coeficienți de reflexie și transmisie Fresnel corespunzători apar în cazul straturilor subțiri și al structurilor multistrat. Pentru a defini corect fasciculul reflectat sau transmis, trebuie urmărită faza relativă a fiecărei componente luminoase. Grosimea de fază a peliculei se determină astfel după cum urmează:
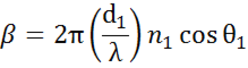
Când mai multe unde luminoase se suprapun, apare o interferență care depinde de faza relativă a fiecărei unde luminoase individuale. Figura de mai jos prezintă combinația undelor luminoase din fasciculul reflectat și calculele Fresnel corespunzătoare acestora.
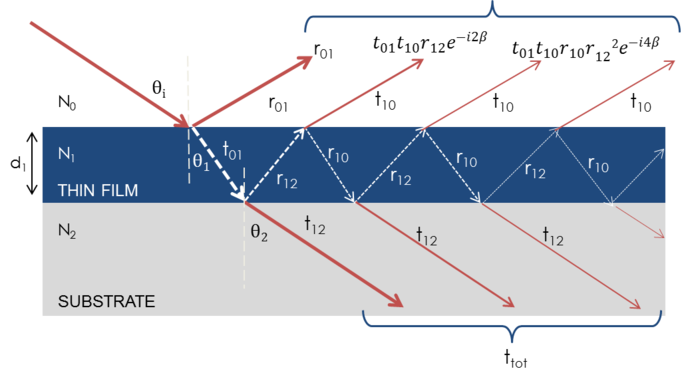
Figura 7: Lumina se reflectă și se refractă la fiecare interfață individuală, ceea ce duce la fascicule multiple într-un film subțire. Interferența fasciculelor depinde de faza și amplitudinea relativă a câmpurilor electrice. Reacția fasciculului poate fi calculată cu ajutorul coeficienților de reflexie și transmisie Fresnel.
Măsuri
Ellipsometria măsoară în principal modul în care componentele p și s reacționează una față de cealaltă în timpul reflexiei sau transmiterii. Așadar, un fascicul de referință face întotdeauna parte din experiment. O polarizare cunoscută este reflectată sau transmisă de la probă și se măsoară polarizarea de ieșire. Modificarea polarizării reprezintă măsurarea elipsometriei:
![]()
Figura 6 prezintă o măsurătoare elipsometrică tipică a eșantionului. Lumina incidentă liniară are ambele componente p- și s-. Lumina reflectată prezintă atât modificări de amplitudine, cât și de fază pentru lumina polarizată p- și s-. Aceste modificări sunt măsurate prin elipsometrie.

Pentru a colecta date de elipsometrie sunt necesare următoarele: sursă de lumină, generator de polarizare, eșantion, analizor de polarizare și detector. Atât generatorul de polarizare, cât și analizorul sunt alcătuite din piese optice care manipulează polarizarea: compensatoare, polarizatoare și modulatoare de fază. Configurațiile tipice ale elipsometrului încorporează un analizor rotativ (RAE), un polarizator rotativ (RPE), un compensator rotativ (RCE) și un modulator de fază (PME). Figura de mai jos prezintă o configurație RAE.
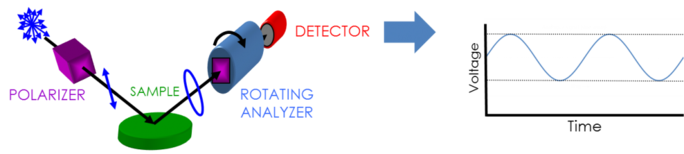
Lumina nepolarizată este produsă de o sursă de lumină și apoi trimisă printr-un polarizator. Polarizatorul este setat pentru a lăsa să treacă doar lumina cu o anumită orientare a câmpului electric. Deoarece axa polarizatorului este aliniată între planurile p- și s-, ambele ajung la suprafața probei. Lumina acum polarizată liniar este reflectată de suprafața probei, devenind astfel polarizată eliptic, și apoi trimisă printr-un polarizator care se rotește continuu („analizor”). Cantitatea de lumină care este lăsată să treacă depinde de orientarea polarizatorului în raport cu elipsa câmpului electric al probei. Pentru a defini polarizarea reflectată, lumina este convertită într-un semnal electronic în detector. Compararea acestor date cu polarizarea de intrare stabilită oferă informații despre modificarea cauzată de reflexia probei: măsurarea elipsometrică a Psi și Delta.
Analiză de date
Ellipsometria este utilizată pentru a defini grosimea peliculei de material sau constantele optice prin măsurarea modificărilor polarizării luminii. Constantele optice „pseudo” din măsurarea elipsometriei pot fi derivate prin inversarea datelor determinate pentru o singură reflexie. Acest lucru este util pentru materiale masive.
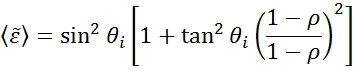
Ecuația de mai sus nu contează cu niciun strat de suprafață. Cu toate acestea, există în mod normal un oxid de suprafață sau o rugozitate în materialele în vrac. O inversiune directă va include aceste date ca parte a constantelor optice masive. A se vedea fig. 10 pentru o prezentare generală a unui proces tipic de analiză a datelor utilizat în măsurătorile elipsometrice. Deoarece nu se poate scrie o ecuație exactă, este necesară o analiză de regresie. Răspunsul este adesea supradeterminat cu doar câteva necunoscute și sute de puncte de date experimentale. O analiză de regresie permite ca toate datele măsurate să fie incluse atunci când se determină soluția.
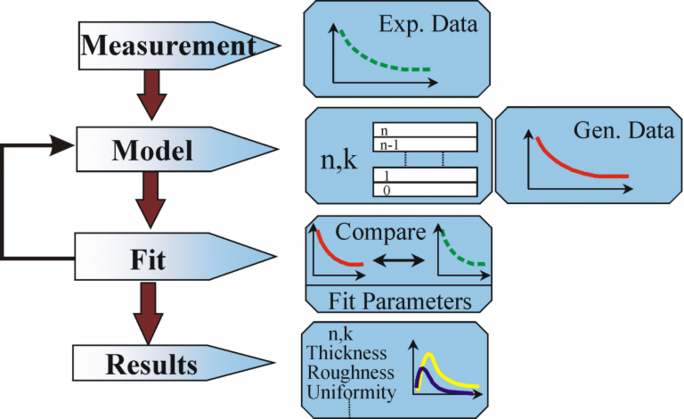
Figura 10: Diagramă de flux pentru analiza datelor de elipsometrie.
Pentru analiza datelor se folosește următoarea procedură: se măsoară proba și se realizează un model al acesteia. Cu ajutorul acestui model se calculează rezultatele presupuse de ecuațiile lui Fresnel, care descriu grosimea și constantele optice ale fiecărui material. Se face o evaluare a calculului preliminar, în cazul în care aceste valori sunt necunoscute. Valorile calculate sunt comparate cu datele experimentale. Pentru o mai bună concordanță între datele experimentale și cele de calcul, datele necunoscute ale materialelor pot fi variate. Cu toate acestea, punctele de date experimentale trebuie să fie întotdeauna mai multe decât parametrii necunoscuți. De exemplu, cu un elipsometru cu o singură lungime de undă pot fi determinate maxim două proprietăți ale materialului, deoarece acesta produce exact două puncte de date: Ψ, Δ (Psi și Delta). Regresia este utilizată pentru a găsi cea mai bună potrivire între model și experiment. Diferența dintre curbele de date este cuantificată cu ajutorul unui estimator, cum ar fi eroarea pătratică medie (MSE). Proprietățile necunoscute sunt variate până când se atinge valoarea minimă a MSE. Aceasta înseamnă că cea mai mică MSE este echivalentă cu cel mai bun răspuns.
Vezi în figura de mai jos curba MSE în funcție de grosimea filmului pentru un film transparent pe siliciu. Cea mai mică valoare MSE apare la o grosime de 749 nm, în ciuda unui număr de minime locale. Prin urmare, grosimea corectă a filmului este, de asemenea, de 749 nm. Algoritmul de regresie ar putea considera că un minim local este corect. Astfel, pentru a determina minimul global corect, este înțelept să se compare rezultatele cu ochiul liber pentru cel mai mic MSE.
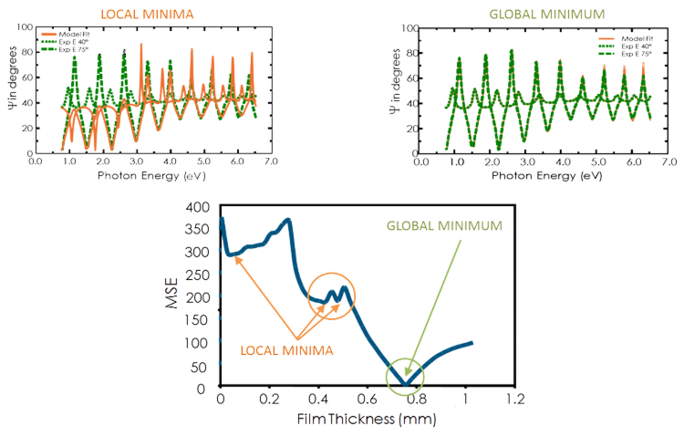
Figura 11, sus-dreapta: Date experimentale și curbele corespunzătoare generate pentru modelul la minimul global. Figura 11, sus-stânga: O curbă similară la minimul local în apropierea unei grosimi de 0,45 µm poate fi ușor identificată ca rezultat incorect. Figura 11, jos: Curba MSE în funcție de grosime arată minimul global. Un algoritm de regresie poate oferi minime locale, dar nu și rezultatul final.
Determinarea grosimii peliculei
Grasimea peliculei este determinată, de obicei, prin interferența dintre lumina care se reflectă de la suprafață și lumina care călătorește prin peliculă. Faptul că această interferență este considerată constructivă sau distructivă depinde de faza relativă a luminii care se unește cu reflexia de la suprafață. Interferența include atât informații de amplitudine, cât și de fază. Informația de fază de la Δ este foarte sensibilă la pelicule până la grosimea submonocameră. Consultați figura de mai jos pentru o comparație a intensității reflectate și a elipsometriei pentru aceeași serie de straturi subțiri de SiO2 pe Si. Intensitatea de reflexie pentru fiecare film este aproape aceeași, în timp ce există variații mari în Δ.
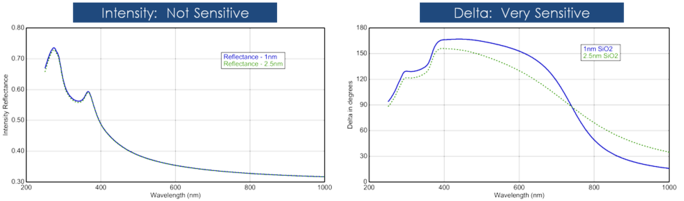
Figura 12, stânga: Intensitatea reflectată și delta elipsometrică (dreapta) pentru doi oxizi subțiri pe siliciu. Măsurarea intensității nu arată că Delta este foarte sensibilă la pelicule de scară nanometrică.
Elipsometria este folosită în mod obișnuit pentru pelicule cu grosimi de la sub-nanometri până la câțiva microni. În cazul peliculelor mai groase de câteva zeci de microni, oscilațiile de interferență pot fi rezolvate doar cu dificultăți din ce în ce mai mari, cu excepția cazului în care se folosesc lungimi de undă infraroșii mai mari. Acesta este motivul pentru care pentru pelicule mai groase se folosesc în mod normal alte tehnici de măsurare.
Pentru a măsura grosimea, o parte din lumină trebuie să parcurgă întreaga peliculă și apoi să se întoarcă la suprafață. În cazul materialelor care absorb lumina, măsurătorile optice ale grosimii pot fi efectuate numai pe straturi subțiri și semi-opace, cu excepția cazului în care sunt efectuate pe regiuni spectrale cu absorbție mai mică. De exemplu, o peliculă organică care absoarbe lumina UV și IR poate fi transparentă la lungimi de undă medii vizibile. Metalele absorb puternic la toate lungimile de undă, astfel încât grosimea maximă a stratului care poate fi determinată se situează în jurul valorii de 100 nm.
Constante optice
Constantele optice joacă un rol important pentru măsurătorile de grosime. Grosimea unei pelicule influențează lungimea drumului luminii care călătorește prin peliculă, iar indicele determină viteza undei luminoase și unghiul de refracție. Prin urmare, ambele contribuie la întârzierea dintre lumina care călătorește prin peliculă și reflecția la suprafață. Este necesar să se stabilească n și k, precum și grosimea, pentru a obține rezultate corecte dintr-o măsurătoare optică.
Deoarece constantele optice ale unui material variază pentru diferite lungimi de undă, toate lungimile de undă care sunt analizate cu elipsometrul trebuie să fie determinate individual. Răspunsul unui material la fiecare lungime de undă poate fi anticipat prin utilizarea unui tabel de constante optice. Pentru a evita ajustarea minuțioasă a constantelor optice necunoscute, lungime de undă cu lungime de undă, este avantajos să se utilizeze simultan toate lungimile de undă. Parametrii ajustabili ai unei relații de dispersie, de exemplu, permit ca forma generală a constantei optice să corespundă rezultatelor experimentale. În comparație cu ajustarea valorilor individuale n și k pentru fiecare lungime de undă, numărul parametrilor liberi necunoscuți este redus considerabil.
Relațiile Cauchy sau Sellmeier sunt utilizate frecvent pentru a descrie indicele pentru materiale transparente, unde relația Cauchy este dată în mod normal sub forma:
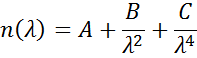
cu cei trei termeni ajustați pentru a se potrivi cu indicele de refracție pentru materialul respectiv. Relația Cauchy nu este limitată de consistența Kramers-Kronig (KK) și poate duce la o dispersie nefizică. Pe de altă parte, relația Sellmeier impune consistența Kramers-Kronig (KK), care garantează că dispersia optică păstrează o formă realistă. Relația Sellmeier se scrie de obicei sub forma:
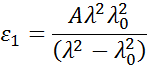
Materialele absorbante au adesea o regiune de lungime de undă transparentă care poate fi modelată cu relația Cauchy sau Sellmeier. În timp ce regiunea de absorbție, cu toate acestea, trebuie să țină cont atât de constantele optice reale, cât și de cele imaginare. Pentru a descrie absorbția pentru diferite materiale, multe relații de dispersie utilizează teoria oscilatorului, inclusiv teoria lui Lorentz, armonică și Gauss. Toate acestea au atribute similare, caracteristicile de absorbție fiind descrise cu Amplitudine, lărgire și energie centrală (legată de frecvența luminii). Forma componentei reale este calculată cu ajutorul consistenței Kramers-Kronig după ce comportamentul imaginar este descris de oscilator. Pentru a include o eventuală absorbție suplimentară în afara regiunii spectrale măsurate, se adaugă un decalaj la componenta reală. Oscilatorul Lorentz poate fi scris ca:
![]()
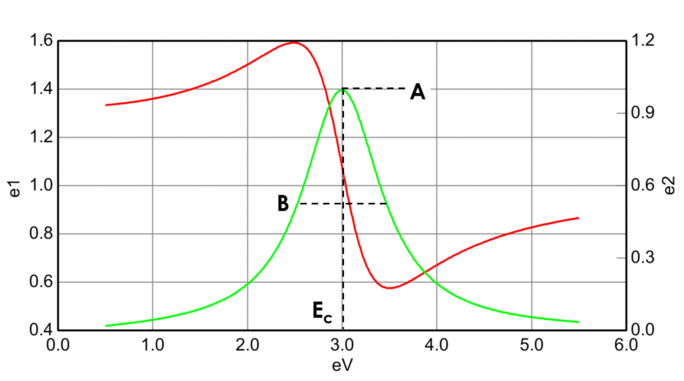
Figura 13 prezintă, de asemenea, Amplitudinea (A), lărgirea (B), energia centrală (Ec) și decalajul (e1, off set) pentru un oscilator Lorentz tipic. Energia E este legată de frecvența unei unde, n:
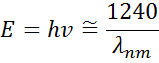
Constanta lui Planck h și lungimea de undă λ sunt date în nanometri. Alte modele de dispersie, cum ar fi Tauc-Lorentz și Cody-Lorentz, încorporează termeni pentru a descrie energia benzii interzise.
Lecturi suplimentare
Ellipsometria este o tehnică optică consacrată pentru măsurarea filmelor subțiri și a materialelor în vrac. Folosește schimbările de polarizare cauzate de reflexia/transmisia dintr-o structură materială pentru a determina caracteristicile materialului, cum ar fi grosimea și constantele optice.
Aspnes D.E. (1985). The Accurate Determination of Optical Properties by Ellipsometry (Determinarea precisă a proprietăților optice prin elipsometrie). În: E: Palik E.D. (ed.) Handbook of Optical Constants of Solids, pp. 89-112. Academic Press, Orlando.
Azzam R.M.A. și Bashara N.M. (1987). Ellipsometry and Polarized Light, Elsevier Science B.V., Amsterdam, Olanda.
Boccara A.C., Pickering C., and Rivory J. (eds.), (1993). Spectroscopic Ellipsometry, Elsevier Publishing, Amsterdam.
Collins R.W., Aspnes D.E., and Irene E.A. (eds.), (1998). „Proceedings from the Second International Conference on Spectroscopic ellipsometry”. În: „Elicopteroscopia: Thin Solid Films, vols. 313-314.
Fujiwara H., Spectroscopic Ellipsometry, Principles and Applications, John Wiley & Sons, Ltd. (în engleză). 2007
Gottesfeld S., Kim Y.T., și Redondo A. (1995). „Recent applications of ellipsometry and spectroellipsometry in electrochemical systems”, În: In: I. Rubinstein (ed.), Physical Electrochemistry: Principles, Methods, and Applications, Marcel Dekker, New York.
Herman, I.P. (1996). Optical Diagnostics for Thin Film Processing, pp 425-479. Academic Press, San Diego, California.
Johs B. et al. (1999). „Overview of Variable Angle Spectroscopic Ellipsometry (VASE), Part II: Advanced Applications”. Optical Metrology, vol. CR72, pp 29-58. SPIE, Bellingham, Washington.
Johs B. et al. (2001). „Recent Developments in Spectroscopic Ellipsometry for in situ Applications”. In: Duparré A, Singh B (ed.) Optical Metrology Roadmap for the Semiconductor, Optical, and Data Storage Industries II, vol. 4449, pp. 41-57. SPIE, Bellingham, Washington.
Roseler A. (1990). Infrared Spectroscopic Ellipsometry, Akademie-Verlag, Berlin.
Rossow U. și Richter W. (1996). „Spectroscopic Ellipsometry” în: „Spectroscopic Ellipsometry” în: Bauer G și Richter W (eds.) Optical Characterization of Epitaxial Semiconductor Layers, pp. 68-128, Springer-Verlag, Berlin.
Tompkins H.G. (1993). A User’s Guide to Ellipsometry, Academic Press, San Diego, California.
Tompkins H.G. și McGahan W.A. (1999). Spectroscopic Ellipsometry and Reflectometry, John Wiley & Sons, Inc., SUA.
Tompkins, H.G. și Irene E.A. (eds.), 2005, Handbook of Ellipsometry, William Andrew Publishing, New York.
Tompkins, H. G. și Hilfiker, J. H., Spectroscopic Ellipsometry, Practical Application to Thin Film Characterization, 2016, Momentum Press Engineering
Woollam J.A. și Snyder P.G. (1992). „Variable Angle Spectroscopic Ellipsometry” (Ellipsometrie spectroscopică cu unghi variabil) în: „Variable Angle Spectroscopic Ellipsometry”: Brundle CR, Evans CA și Wilson S (eds) Encyclopedia of Materials Characterization: Surfaces, Interfaces, Thin Films, pp. 401-411, Butterworth-Heinemann, Boston.
Woollam J.A. et al (1999). „Overview of Variable Angle Spectroscopic Ellipsometry (VASE), Part I: Basic Theory and Typical Applications”. Optical Metrology, vol. CR72, pp 3-28. SPIE, Bellingham, Washington.
Woollam J.A. (2000). „Ellipsometry, Variable Angle Spectroscopic”, în: „Ellipsometry, Variable Angle Spectroscopic”, în: „Ellipsometry, Variable Angle Spectroscopic: Webster J.G. (ed.) Wiley Encyclopedia of Electrical and Electronics Engineering, pp. 109-116. John Wiley & Sons, New York.
.