Cum se calculează tensiunea în frânghiile care suspendă un obiect
Vezi în ilustrația de mai jos că forța, F, necesară pentru a ridica obiectul este egală cu greutatea, W, a obiectului. Această idee este conceptul fundamental care stă la baza formulei noastre de forță de tensiune. Tot mai jos este prezentată și diagrama de corp liber a obiectului care arată forțele de tensiune, T, care acționează în coardă. După cum puteți vedea, forțele de tensiune vin în perechi și în direcții opuse:
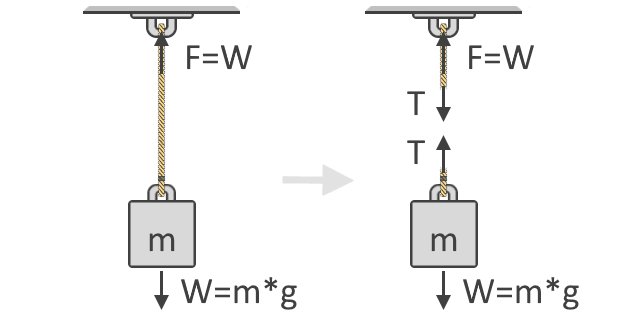
În conformitate cu a doua lege a mișcării a lui Newton, putem exprima apoi suma forțelor folosind diagrama de corp liber a obiectului, așa cum se arată în partea dreaptă a ilustrației de mai sus. Folosim diagramele de corp liber pentru a arăta diferitele direcții și mărimi ale forțelor care acționează asupra unui corp. În echilibru, toate aceste forțe ar trebui să fie egale cu zero. Considerând toate forțele ascendente ca fiind pozitive și cele descendente ca fiind negative, ecuația noastră este:
ΣF = 0 = T + (-W)T = W
unde greutatea, W, devine negativă, deoarece este îndreptată în jos. Prin transpunerea lui W în cealaltă parte a ecuației, putem vedea acum că forța de tensiune din frânghie este egală cu greutatea obiectului pe care îl transportă, așa cum am arătat și mai sus.
Dacă folosim mai multe frânghii pentru a ridica obiectul, forța totală de tensiune se împarte între frânghii. Forța de tensiune din fiecare frânghie depinde de unghiurile lor față de direcția forței căreia i se opune. Pentru a înțelege mai bine acest lucru, să luăm în considerare o altă diagramă de corp liber a unui obiect suspendat de două frânghii, așa cum se arată mai jos:
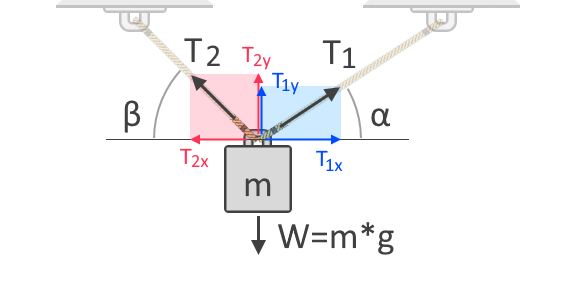
În diagrama de corp liber prezentată mai sus, putem vedea componentele orizontală și verticală ale forțelor de tensiune, T₁, și T₂. Forțele sunt vectoriale, ceea ce înseamnă că ele au întotdeauna atât mărimi, cât și direcții. La fel ca toți vectorii, forțele pot fi exprimate în aceste componente care oferă influența forței de-a lungul axelor orizontală și verticală. T₁ₓ și T₂ₓ sunt componentele verticale ale lui T₁ și, respectiv, T₂. Pe de altă parte, T₁ᵧ și T₂ᵧ sunt componentele verticale ale acelorași forțe, respectiv T₂ᵧ. Deoarece gravitația acționează asupra obiectului pe axa verticală, trebuie să luăm în considerare componentele verticale ale forțelor de tensiune pentru însumarea forțelor noastre, după cum urmează:
ΣF = 0 = T₁ᵧ + T₂ᵧ + (-W)W = T₁ᵧ + T₂ᵧ
Pentru că știm și unghiurile forțelor de tensiune, putem exprima T₁ᵧ și T₂ᵧ în termeni de T₁ și, respectiv, T₂, cu ajutorul funcțiilor trigonometrice:
T₁ᵧ = T₁ * sin(α)T₂ᵧ = T₂ * sin(β)W = T₁ * sin(α) + T₂ * sin(β)
Potem spune, de asemenea, că pentru ca sistemul să fie în echilibru, obiectul nu trebuie să se deplaseze pe orizontală sau de-a lungul axei x. Prin urmare, componentele orizontale ale T₁ și T₂ trebuie atunci să fie egale cu zero. De asemenea, cu ajutorul trigonometriei, putem exprima T₁ₓ și T₂ₓ în termeni de T₁ și, respectiv, T₂₂:
T₁ₓ = T₂ₓT₁ * cos(α) = T₂ * cos(β)
Dacă împărțim ambele părți cu cos(α), obținem o ecuație în care T₁ se exprimă în funcție de T₂ și de unghiuri:
T₁ = T₂ * cos(β) / cos(α)
Apoi putem folosi această ecuație pentru a rezolva T₂ înlocuind T₂ * cos(β) / cos(α) ca T₁ în ecuația noastră de însumare a forțelor, așa cum se arată mai jos:
W = T₁ * sin(α) + T₂ * sin(β)W = T₂ * * sin(α) + T₂ * sin(β)W = T₂ * T₂ = W /
În cele din urmă, dacă înmulțim întreaga ecuație cu cos(β) / cos(α), așa cum am derivat în valoarea lui T₁ în termeni de T₂, și apoi simplificăm totul, obținem această ecuație:
T₁ = W / * T₁ = W / * T₁ = W /
Acum tot ce trebuie să știți sunt unghiurile frânghiilor de tensiune în raport cu orizontala. Dacă este dat un unghi față de verticală, trebuie doar să scădem acest unghi din 90°. Procedând astfel, veți obține unghiul față de orizontală. Cu toate acestea, dacă vi se dau alte valori ale unghiurilor care pot fi mai mari de 90° sau chiar 180°, ar fi bine să consultați calculatorul nostru de unghiuri de referință pentru a vă ajuta să determinați unghiul de care aveți nevoie. După ce am determinat valorile pentru variabilele din formulele noastre de forță de întindere, putem acum să rezolvăm forțele de întindere.
.