Cât de multe știți despre infinit? Probabil că ați auzit de un număr care este cel mai mare număr posibil, sau imposibil de mare.
Pentru a explica infinitele, trebuie mai întâi să definesc o anumită terminologie.
Integrii sunt numere folosite pentru numărare. Ansamblul numerelor întregi este definit ca fiind toate numerele fără componente fracționare. Câteva exemple sunt: -12, 0, 0, 1, 3, 42, 17.
Infinitul este conceptul de obiect aflat dincolo de raza de acțiune a numerelor naturale. A fost conceptualizat pentru prima dată de un matematician rus pe nume Georg Cantor, care nu numai că a introdus infinitul, dar a și dezvăluit că există mai multe infinituri care există.
Cantor a furnizat o dovadă controversată a infinitului, care spunea că unele infinituri sunt mai mari decât altele. La început, acest lucru poate părea imposibil – cum poate un obiect să fie mai mare decât un alt obiect care este infinit?

Cantor și-a bazat dovada pe o ramură a Matematicii care este aparent inutilă: Teoria seturilor. Un set este o colecție de obiecte – de exemplu, putem avea un set care conține 1, 2 și 3. Aceste obiecte din set se numesc elemente.
În notație matematică, aceasta ar arăta astfel:
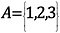
Numărul de elemente din acest set, sau cardinalitatea setului, este 3.
Acesta se notează ca:
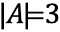
Dacă avem acum un alt ansamblu, B, care conține obiecte, astfel încât
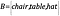
Cum știm că ansamblurile au aceeași dimensiune?
Un mod în care putem vedea acest lucru este prin numărarea numărului de elemente din cel de-al doilea set. Putem vedea clar că și acest set are 3 elemente în el și astfel știm că au aceeași dimensiune.
Un alt mod în care putem face acest lucru este comparând al doilea set, B, cu primul set, A, prin cartografiere.
Potem cartografia primul element din setul A , 1, cu primul element din setul B, scaun.
Pot fi mapat al doilea element din setul A, 2, pe al doilea element din setul B, masă.
Pot fi mapat al treilea element din setul A, 3, pe al treilea element din setul B, pălărie.
Din moment ce fiecare element din A este mapat pe exact 1 element din B, seturile au dimensiuni egale.
Să ne uităm acum la seturile infinite. Setul de numere întregi, care a fost menționat la început, este un set infinit – există un număr infinit de numere întregi. Setul de numere întregi este notat cu simbolul
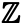
Set de numere pare, pe care îl putem nota ca
este definit ca
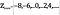
Intuitiv, se poate părea că
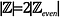
din moment ce există 2 numere întregi pentru fiecare număr întreg par: 1 număr întreg impar și 1 număr întreg par. Să verificăm acest lucru.
Să încercăm să comparăm seturile prin maparea elementelor din 1 set în celălalt.
Pot fi mapate 1 în 2, 2 în 4, 3 în 6, și așa mai departe.
Dacă acest lucru continuă în toate seturile, putem vedea că fiecare element din setul de numere întregi se mapează pe exact 1 element din setul de numere întregi pare.
Așa, deși poate părea contra-intuitiv, mărimea seturilor sunt egale.
.