A variância é um número que indica até que ponto um conjunto de números está separado.
Variância – Exemplo
Um estudo tem 100 pessoas realizando uma tarefa simples de velocidade durante 80 tentativas. Para cada participante, 80 tempos de reacção (em segundos) são assim registados. Parte desses dados são mostrados abaixo.

Em estudos como esses, normalmente vemos que as pessoas ficam mais rápidas à medida que executam a tarefa de velocidade com mais frequência. Ou seja, o tempo médio de reação tende a diminuir ao longo das tentativas.
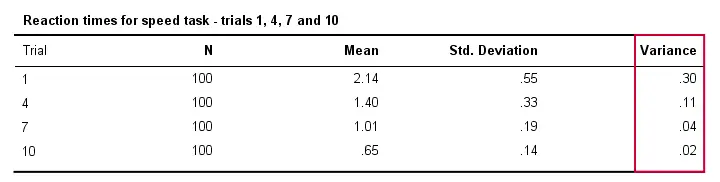
Tanto assim, os tempos de reação tipicamente variam menos entre diferentes pessoas na medida em que elas executam a tarefa com mais freqüência. Tecnicamente, dizemos que a variância diminui ao longo das experiências. A tabela abaixo ilustra isto para os ensaios 1,4,7 e 10,
Variância e Histograma
Uma ótima maneira de visualizar os dados da nossa tabela anterior é um histograma para cada ensaio. Assim, a figura abaixo ilustra que os participantes foram mais rápidos nos ensaios; do ensaio 1 ao ensaio 10 as barras do histograma movem-se para a esquerda, para 0 segundos.
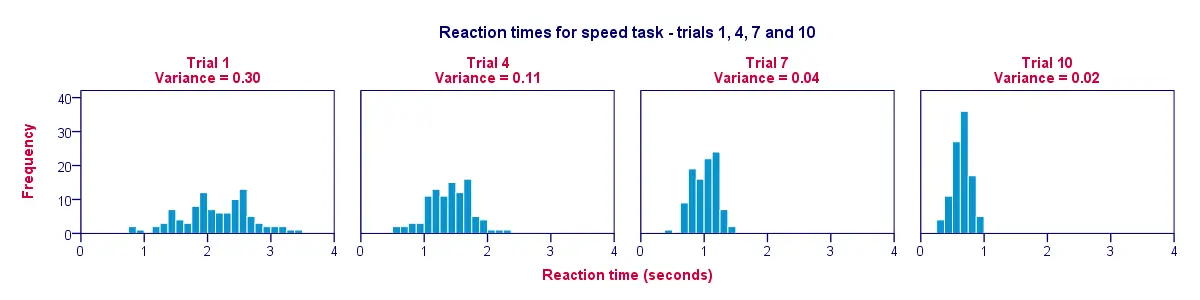
Um segundo achado é que os histogramas se tornam mais estreitos (e portanto mais altos) à medida que passamos do ensaio 1 para o ensaio 10; isto ilustra que os tempos de reacção variam cada vez menos entre os nossos participantes à medida que o ensaio avança. A variância diminui ao longo dos ensaios.
Variância – Fórmula Populacional
Uma fórmula básica para calcular a variância é
$$S^2 = \frac{\sum(X – \ sobrelinha{X})^2}{n}$$$
A fórmula básica para calcular a variância é
A fórmula básica para calcular a variância é Portanto, vamos demonstrá-la em um punhado de dados.
Variância – GoogleSheets
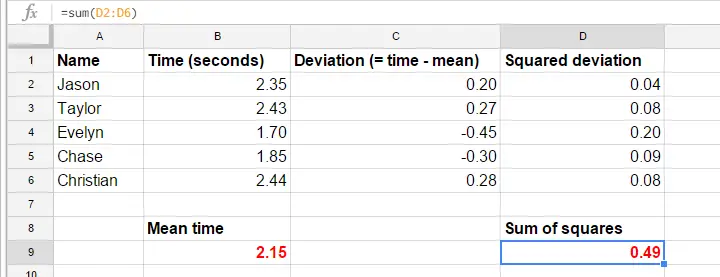
Por uma questão de simplicidade, vamos cortar os nossos dados para o primeiro ensaio para os primeiros 5 participantes. Estes 5 tempos de reacção – e um cálculo manual da sua variância – estão neste GoogleSheet.
Variância – Passos de Cálculo
As fórmulas no GoogleSheet mostram precisamente como calcular uma variância. Os passos básicos são
- calcular o tempo médio de reação (2,15);
- calcular escores de desvio (tempo de reação menos tempo médio de reação);
- calcular escores de desvio ao quadrado;
- add escores de desvio ao quadrado. O resultado (0,49) é uma soma de quadrados, o bloco principal da ANOVA;
- divide a soma dos quadrados pelo número de observações (5 tempos de reação).
Alternativamente, calcule uma variância digitando =VARP(B2:B6) em alguma célula (B2:B6 são as células que seguram nossos 5 tempos de reação). VARP é a abreviação de “população de variância”. OpenOffice e MS Excel contêm fórmulas semelhantes.
Variância – Fórmula Amostra
Simplesmente ao desvio padrão, se nossos dados são uma amostra aleatória simples de uma população muito maior, a fórmula acima mencionada subestimará sistematicamente a variância da população. Neste caso usaremos uma fórmula ligeiramente diferente:
$$S^2 = \frac{\sum(X_i – \overline{X})^2}{n – 1}$$
Que fórmula usar assim depende dos nossos dados: eles contêm toda a população que gostaríamos de investigar ou são uma mera amostra desta população?
Desde que os nossos 100 participantes sejam claramente uma amostra, usaremos a fórmula da amostra. No GoogleSheets, digitando =VAR(B2:B6) em alguma célula retornará a variância da amostra.
Variância em SPSS
Segundo sabemos, a fórmula para a variância da população está completamente ausente do SPSS e consideramos isto uma falha grave. Em vez disso, o SPSS usa sempre a fórmula da amostra, tanto para a variância entre sujeitos (discutida neste tutorial) como para a variância dentro dos sujeitos. O output relevante é mostrado abaixo.

Reglar esta tabela de output, observe também que a variância é de fato o desvio padrão ao quadrado (além de arredondamento).
Reglar a variância, isso é tudo. Esperamos que você tenha achado este tutorial útil para entender o que é uma variância.