Quanto você sabe sobre infinitos? Você provavelmente já ouviu falar de um número que é o maior número possível, ou impossivelmente grande.

>

Para explicar infinitos, preciso primeiro definir alguma terminologia.

Integers são números usados para a contagem. O conjunto de números inteiros é definido como todos os números sem componentes fracionários. Alguns exemplos são: -12, 0, 1, 3, 42, 17.

Infinito é o conceito de um objeto além do alcance dos números naturais. Ele foi inicialmente conceituado por um matemático russo chamado Georg Cantor, que não só introduziu o infinito, mas também revelou que existiam múltiplos infinitos.

Cantor forneceu uma prova controversa de infinitos, que dizia que alguns infinitos eram maiores que outros. A princípio, isto pode parecer impossível – como pode um objecto ser maior que outro objecto que é infinito?

Cantor baseou a sua prova num ramo da Matemática que é aparentemente inútil: Teoria do Set. Um conjunto é uma coleção de objetos – por exemplo, podemos ter um conjunto contendo 1, 2 e 3. Estes objetos do conjunto são chamados de elementos.

Na notação matemática, isto pareceria:

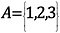
O número de elementos deste conjunto, ou a Cardinalidade do conjunto, é 3.

Este é indicado como:

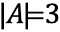
Se agora temos outro conjunto, B, contendo objetos, tais que

>

>

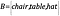9047>

Como sabemos que os conjuntos têm o mesmo tamanho?

Uma maneira de vermos isso é contando o número de elementos no segundo conjunto. Podemos ver claramente que este conjunto também tem 3 elementos, e assim sabemos que eles têm o mesmo tamanho.

Uma outra maneira de fazer isso é comparando nosso segundo conjunto, B, com o nosso primeiro conjunto, A pelo mapeamento.

Podemos mapear o primeiro elemento do conjunto A , 1, para o primeiro elemento do conjunto B, cadeira.

Podemos mapear o segundo elemento do conjunto A, 2, para o segundo elemento do conjunto B, tabela.

Podemos mapear o terceiro elemento do conjunto A, 3, para o terceiro elemento do conjunto B, chapéu.

Desde que todos os elementos do conjunto A sejam mapeados para exatamente 1 elemento do conjunto B, os conjuntos têm o mesmo tamanho.

Vamos agora dar uma olhada em conjuntos infinitos. O conjunto de números inteiros, que foi mencionado no início, é um conjunto infinito – há um número infinito de números inteiros. O conjunto de números inteiros é denotado pelo símbolo

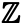
O conjunto de números pares, que podemos denotar como

é definido como

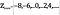
Intuitivamente, pode parecer como

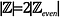
, pois há 2 números inteiros para cada número inteiro uniforme: 1 número inteiro ímpar e 1 número inteiro par. Vamos verificar isto.

Tentemos comparar os conjuntos mapeando elementos de 1 conjunto para o outro.

Podemos mapear 1 para 2, 2 para 4, 3 para 6, e assim por diante.

Se isto continuar ao longo dos conjuntos, podemos ver que todos os elementos do conjunto inteiro se mapeia para exactamente 1 elemento do conjunto inteiro par.

Assim, embora possa parecer contra-intuitivo, o tamanho dos conjuntos são iguais.