Convolução indesejada é um problema inerente na transferência de informação analógica. Por exemplo, tudo o que se segue pode ser modelado como uma convolução: embaçamento de imagem em uma câmera trêmula, ecos em chamadas telefônicas de longa distância, a largura de banda finita dos sensores analógicos e eletrônicos, etc. Deconvolução é o processo de filtrar um sinal para compensar uma convolução indesejada. O objetivo da deconvolução é recriar o sinal tal como existia antes daconvolução ter ocorrido. Isto normalmente requer que as características daconvolução (isto é, a resposta de impulso ou frequência) sejam conhecidas. Isto pode se distinguir da deconvolução cega, onde as características da convolução parasitária não são conhecidas. A deconvolução cega é um problema muito mais difícil que não tem solução geral, e a abordagem deve ser adaptada para a aplicação particular.
Deconvolução é quase impossível de entender no domínio do tempo, mas desiste da restrição de velocidade no domínio da frequência. Cada sinusoidal que compõe o sinal original pode ser alterado em amplitude e/ou fase à medida que passa pela convolução indesejada. Para extrair o sinal original, o filtro de desconvolução deve desfazer essas mudanças de amplitude e fase. Para
exemplo, se a convolução altera a amplitude de um sinusoidal em 0.5 com uma mudança de fase de 30 graus, o filtro de deconvolução deve amplificar o sinusoidal em 2.0 com uma mudança de fase de -30 graus.
O exemplo que usaremos para ilustrar a deconvolução é um detector de raios gama. Como ilustrado na Fig. 17-3, este dispositivo é composto de duas partes, um cintilador e um detector de luz. Um cintilador é um tipo especial de material transparente, tal como iodeto de sódio ou germanato de bismuto. Estes compostos alteram a energia em cada raio gama para uma breve explosão de luz visível. Esta luz
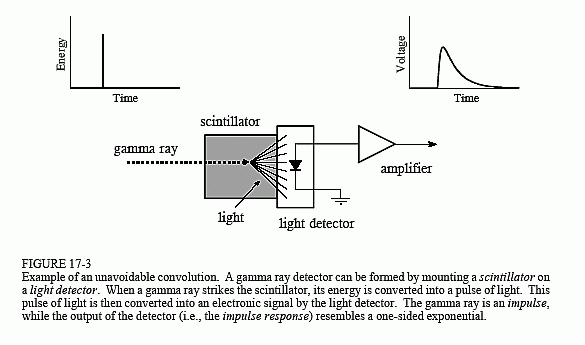
é então convertida num sinal electrónico por um detector de luz, tal como um aphotodiodo ou um tubo fotomultiplicador. Cada pulso produzido pelo detector assemelha-se a um exponencial unilateral, com alguns arredondamentos dos cantos. A forma é determinada pelas características do cintilador utilizado. Quando o raio agamma deposita a sua energia no cintilador, os átomos próximos são excitados a um nível de energia mais elevado. Estes átomos são aleatoriamente deexcitados, cada um produzindo um único fóton de luz visível. O resultado líquido é um pulso de luz cuja amplitude decai por algumas centenas de nanossegundos (para o iodeto de sódio). Uma vez que a chegada de cada raio gâmico é um impulso, o pulso de saída do detector (ou seja, o exponencial unilateral) é a resposta de impulso do sistema.
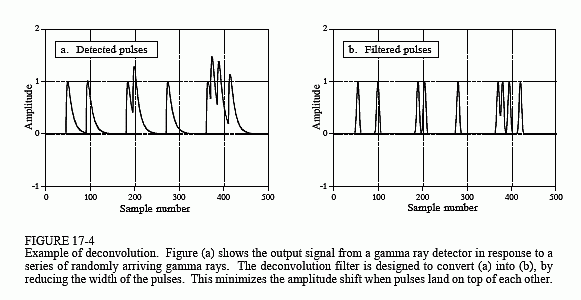
Figure 17-4a mostra pulsos gerados pelo detector em resposta a raios gama de chegada aleatória. A informação que gostaríamos de extrair deste sinal de saída é a amplitude de cada pulso, que é proporcional à energia do raio gama que o gerou. Esta informação é útil porque a energia canta coisas interessantes sobre onde o raio gama tem estado. Por exemplo, pode fornecer informação médica sobre um paciente, dizer a idade de uma galáxia distante, detectar uma bomba na bagagem de avião, etc.
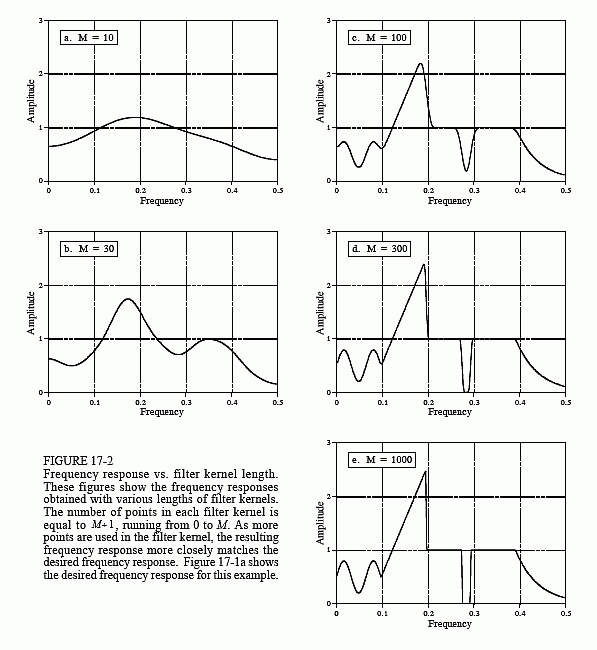
Todos os dados ficariam bem se apenas um raio gama ocasional fosse detectado, mas este não é geralmente o caso. Como mostrado em (a), dois ou mais pulsos podem se sobrepor, deslocando a amplitude medida. Uma resposta a este problema é desconectar o sinal de saída do detector, tornando os pulsos mais estreitos para que menos empilhamento ocorra. Idealmente, gostaríamos que cada pulso se assemelhasse ao impulso original. Assim você pode suspeitar, isso não é possível e devemos nos contentar com um pulso que seja de comprimento finito, mas significativamente menor do que o pulso detectado. Este objetivo é ilustrado na Fig. 17-4b.
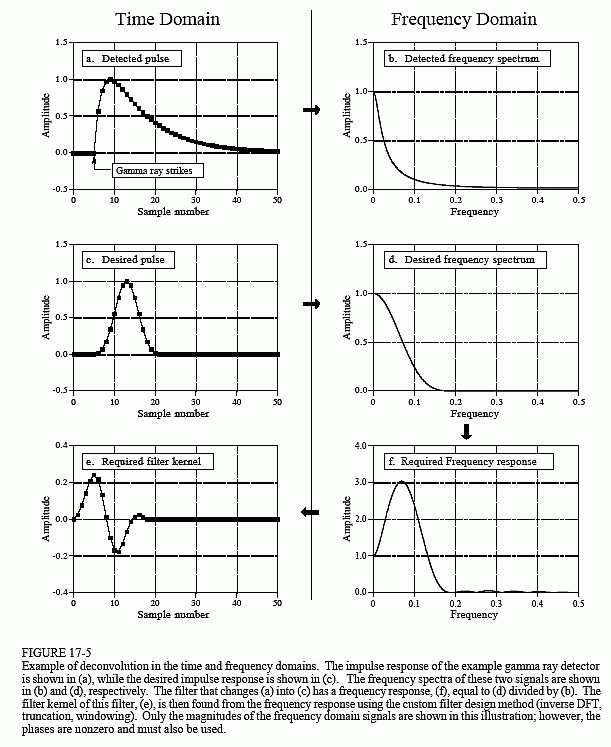
Even embora o sinal do detector tenha sua informação codificada no domínio do tempo, grande parte de nossa análise deve ser feita no domínio da freqüência, onde o problema é mais fácil de entender. Figura 17-5a é o sinal produzido pelo detector (algo que nós conhecemos). Figura (c) é o sinal que desejamos ter (também algo que sabemos). Este pulso desejado foi arbitrariamente selecionado para ter a mesma forma asa janela Blackman, com um comprimento de cerca de um terço do pulso original. Nosso objetivo é encontrar um kernel de filtro, (e), que ao girar com o sinal em (a), produza o sinal em (c). Na forma de equação: se um * e = c, e dado a e c, finde.
Se esses sinais fossem combinados por adição ou multiplicação em vez de volução, a solução seria fácil: a subtração é usada para “de-add” e a divisão é usada para “de-multiply”. Convolução é diferente; não há uma operação simples e inversa que pode ser chamada de “deconvolução”. A convolução é demasiado confusa para ser desfeita através da manipulação directa dos sinais do domínio do tempo.
Felizmente, este problema é mais simples no domínio da frequência. Lembre-se, a convolução em um domínio corresponde com a multiplicação no outro domínio. Novamente referindo-se aos sinais na Fig. 17-5: se b × f = d, e dado b e d, encontrar f. Este é um problema fácil de resolver: a resposta de freqüência do filtro, (f), é o espectro de freqüência do pulso desejado, (d), dividido pelo espectro de freqüência do pulso detectado, (b). Como o pulso detectado é assimétrico, ele terá uma fase não nula. Isto significa que deve ser usada uma divisão complexa(ou seja, uma magnitude & fase dividida por outra magnitude & fase). Caso você tenha esquecido, o Capítulo 9 define como realizar uma divisão complexa de um espectro por outro. O kernel de filtro requerido, (e), é então encontrado a partir da resposta de frequência pelo método de filtro personalizado (IDFT, shift, truncate, &multiply por uma janela).
Existem limites para a melhoria que a deconvolução pode fornecer. Em outras palavras, se você ficar ganancioso, as coisas vão desmoronar. Ficar ganancioso neste exemplo significa tentar tornar o pulso desejado excessivamente estreito. Vejamos o que acontece. Se o pulso desejado for tornado mais estreito, seu espectro de freqüência deve conter mais componentes de alta freqüência. Como estes componentes de alta freqüência estão em uma amplitude muito baixa no pulso detectado, o filtro deve ter um ganho muito alto nestas freqüências. Por exemplo, (f) mostra que algumas freqüências devem ser multiplicadas por um fator de três para se obter o pulso desejado (c). Se o pulso desejado for tornado mais estreito, o ganho do filtro de deconvolução será ainda maior em freqüências altas.
O problema é que pequenos erros são muito imperdoáveis nesta situação. Por exemplo, se alguma frequência é amplificada em 30, quando apenas 28 é necessária, o sinal de desconvolução provavelmente será uma bagunça. Quando a deconvolução é empurrada para níveis maiores de desempenho, as características da convolução indesejada devem ser entendidas com maior precisão e precisão. Há sempre incógnitas em aplicações do mundo real, causadas por vilões tais como: ruído eletrônico, deriva de temperatura, variação entre dispositivos, etc. Essas incógnitas definem um limite de quão bem a deconvolução irá funcionar.
Se a convolução indesejada for perfeitamente compreendida, ainda há um fator que limita o desempenho da deconvolução: o ruído. Por exemplo, as convoluções mais desejadas tomam a forma de um filtro passa-baixo, reduzindo a amplitude dos componentes de alta freqüência no sinal. A deconvoluçãocorreta isto através da amplificação destas frequências. No entanto, se a amplitude destes componentes cair abaixo do ruído inerente ao sistema, a informação contida nestas frequências é perdida. Nenhuma quantidade de processamento de sinal pode recuperá-la. Desaparece para sempre. Adios! Adeus! Sayonara! Tentar recuperar estes dados só vai amplificar o barulho. Como um caso extremo, a amplitude de algumas frequências pode ser completamente reduzida a zero. Isto não só oblitera a informação, como tentará fazer com que o filtro de deconvolução tenha um ganho infinito nestas frequências. A solução: projetar um filtro de deconvolução menos agressivo e / ou colocar limites sobre quanto ganho é permitido em qualquer uma das freqüências.
Até onde você pode ir? Quão ganancioso é muito ganancioso? Isso depende totalmente do problema que você está atacando. Se o sinal for bem comportado e tiver baixo ruído, provavelmente pode ser feita uma melhoria tão significativa (pense num factor de 5-10). Se o sinal muda com o tempo, não é especialmente bem compreendido, ou é ruidoso, você não vai fazer quase tão bem (pense num fator de 1-2). Uma deconvolução bem sucedida envolve uma grande quantidade de testes. Se funcionar em algum nível, tente ir mais longe; você saberá quando ela se desmoronar. Nenhuma quantidade de trabalho teórico permitirá que você contorne este processo.
Deconvolução também pode ser aplicada a sinais codificados no domínio de frequência. Exemplo clássico é a restauração de gravações antigas do famoso cantor de ópera, Enrico Caruso (1873-1921). Estas gravações foram feitas com equipamentos muito primitivos pelos padrões modernos. O problema mais significativo é o das gravações da longa trompa tubular usada para reunir o som. Sempre que o cantor atinge uma dessas freqüências de ressonância, a intensidade da gravação aumenta abruptamente. A deconvolução digital melhorou a qualidade subjetiva dessas gravações em
reduzindo os pontos altos da música. Descreveremos apenas o método geral; para uma descrição detalhada, veja o artigo original: T. Stockham, T. Cannon, andR. Ingebretsen, “Blind Deconvolution Through Digital Signal Processing”,Proc. IEEE, vol. 63, Abr. 1975, pp. 678-692.
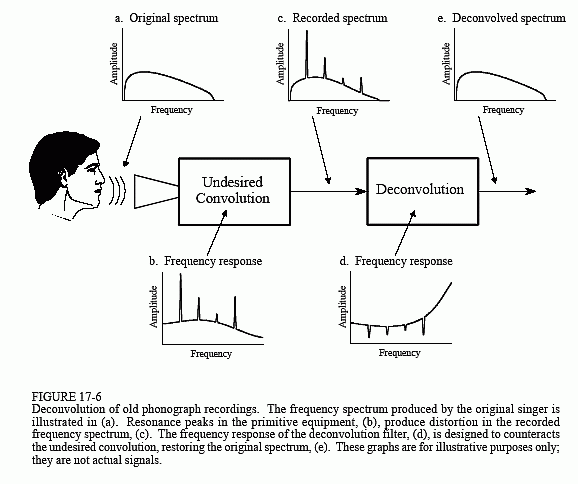
Figure 17-6 mostra a abordagem geral. O espectro de frequência do sinal de áudio teoriginal é ilustrado em (a). A figura (b) mostra a resposta de frequência do aparelho de gravação, uma curva relativamente suave, excepto picos de ressonância transversal agudos. O espectro do sinal gravado, mostrado em (c), é igual ao espectro verdadeiro, (a), multiplicado pela resposta de freqüência desigual, (b). O objetivo da deconvolução é contrabalançar a indesejávelconvolução. Em outras palavras, a resposta de freqüência do filtro de deconvolução,(d), deve ser o inverso de (b). Ou seja, cada pico em (b) é cancelado por um mergulho correspondente em (d). Se este filtro fosse perfeitamente projetado, o sinal resultante teria um espectro, (e), idêntico ao do original.
Aqui está a captura: o aparelho de gravação original há muito tempo foi descartado, e sua resposta de freqüência, (b), é um mistério. Em outras palavras, este é um problema de blinddeconvolution; dado apenas (c), como podemos determinar (d)?
Problemas de deconvolução cega são geralmente atacados fazendo uma estimativa ou um pressuposto sobre os parâmetros desconhecidos. Para lidar com este exemplo, assume-se que o espectro médio da música original corresponde ao espectro médio da mesma música executada por um cantor dos dias de hoje usando o modernequipamento. O espectro médio é encontrado pelas técnicas do Capítulo 9:quebrar o sinal num grande número de segmentos, tomar a DFT de cada segmento, converter em forma polar, e depois calcular a média das magnitudes em conjunto. No caso mais simples, a resposta de frequência desconhecida é tomada como o espectro médio da gravação antiga, dividido pelo espectro médio da gravação moderna. (O método usado por Stockham et al. é baseado numa técnica mais sofisticada de processamento homomórfico, fornecendo uma melhor estimativa das características do sistema de gravação).