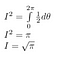O Senhor Kelvin escreveu sobre esta integral: “Um matemático é um para quem isso é tão óbvio como o dobro que dois faz quatro é para ti.”
Desfruta 😉
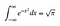 >
>
>
OK, por isso vou assumir que conheces alguma integração e diferenciação básica. O seguinte vai acrescentar alguma intuição a truques inteligentes que virão mais tarde. Não se preocupe se algum deles for um pouco desconcertante, apenas tente sentir o que está acontecendo.
A estratégia aqui será fazer uma substituição inteligente. Mas nós faremos uma substituição em duas variáveis. Você pode visualizar o problema atual como calculando a área sob uma curva
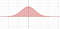
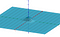
Mas vamos mostrar que o problema pode ser transformado em um de calcular um volume.
>
>
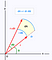
Para calcular o volume, usamos uma mudança ligeiramente diferente da fórmula da variável para o que você usa em integrais normais. Usaremos as coordenadas polares. Isto expressa as coordenadas x e y em termos do seu raio e do seu ângulo. A Geogebra tem uma boa maneira interativa de vê-la aqui

Então vamos usar a mudança mágica da fórmula base para coordenadas polares.
Ao calcular a área sob a curva, tivemos o elemento ‘dx’ que representa uma pequena distância ao longo do eixo x. Ao calcular um volume, temos dx dy, que é como um pequeno retângulo com comprimento lateral dx e dy. Usamos então estas bases para criar uma série de caixas que estimam o volume. Isto é mais fácil de ver com a visualização abaixo. A integral é o limite destas aproximações.
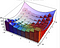
Quando, em vez disso, usamos o sistema de coordenadas polares, temos um elemento de área ligeiramente diferente por baixo. Abaixo, dA é o elemento de área. Com pequenas alterações no ângulo e no raio, este elemento de área pode ser cada vez mais bem aproximado por um rectângulo com comprimentos laterais dr e r*dtheta respectivamente. Se você se sente confortável com alguma geometria, para o pequeno pecado theta (theta) é muito bem aproximado por theta e você pode então provar o resultado abaixo.
Solvendo a integral
Primeiro damos um nome à nossa integral. Chamamos-lhe I.
>
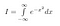
>
Nota que x é apenas uma ‘variável dummy’. A área existe independentemente do nome da variável que usamos. Assim, também podemos escrever as duas seguintes equações
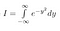
>
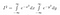
>
>
>
Agora, pois eu sou apenas uma constante, embora ainda não saibamos o valor da mesma, podemos usar nossas regras normais para trazer uma constante dentro de uma integral
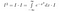
>
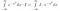
>
Até agora não fizemos muito substantivo. Agora pensamos muito sobre o que significa a integral. Nós tomamos integrais de funções. Se duas funções levam o mesmo valor em todo lugar, elas são as mesmas, e têm a mesma área. Com isso em mente, podemos fazer as seguintes manipulações, se vemos I*exp(-x²) como uma função de x, ou seja, algo que toma valores de x como input, e dá um número como output.
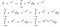
>
Ok, isso foi muito para tomar. Na primeira linha, nós apenas reescrevemos I na sua forma integral com um nome de variável diferente. Na segunda linha, tratando I*exp(-x²) como uma função, percebemos que podemos trazer o exp(-x²) dentro da integral do corante, e isto ainda daria o mesmo valor de saída para qualquer valor de entrada de x. Finalmente, usamos as regras de exponenciação.
Escrevendo isto por extenso, agora temos
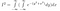
Próximo vem o insight killer. Acima mexemos com nomes de variáveis e como representar uma função. Agora mudamos nossa perspectiva: esta expressão também representa a integral de exp(-(y²+x²)) sobre todo o plano 2D, com o elemento de área dA = dx dy. Ou seja, dx dy é um pequeno retângulo sobre um plano, e exp(-(y²+x²)) é a altura acima desse retângulo.
Próximo, usamos os insights das coordenadas polares de anteriormente
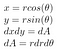 >
>
As sin² + cos² = 1, depois de ligar tudo, nós temos
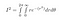
r varia de 0 a infinito e teta varia de 0 a 2*pi, porque isto cobre todo o plano 2D: qualquer ponto tem um raio menor que o infinito, e um ângulo entre 0 e 2pi radiantes.
Podemos avaliar a integral interna usando a regra da corrente
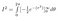
E, na terra prometida, encontramo-nos agora: