Acontecimentos aleatórios que ocorrem no espaço de amostra contínua podem invocar imagens geométricas por pelo menos duas razões: devido à natureza do problema ou devido à natureza da solução.

Alguns problemas, como a agulha de Buffon, Birds On a Wire, Bertrand’s Paradox, ou o problema do bastão quebrado em três peças surgem, pela sua natureza, num cenário geométrico. Este último também admite múltiplas reformulações que requerem a comparação das áreas das figuras geométricas. Em geral, podemos pensar em probabilidades geométricas como quantidades não negativas (não superiores a 1) sendo atribuídas a sub-regiões de um determinado domínio sujeitas a certas regras. Se a função μ é uma expressão dessa atribuição definida num domínio D, então, por exemplo, requeremos

0 ≤ μ(A) ≤ 1, A ⊂ D e
μ(D) = 1

A função μ não é normalmente definida para todos os A ⊂ D. Os subconjuntos de D para os quais μ está definido são os eventos aleatórios que formam um determinado espaço de amostra. Muito frequentemente μ é definido por meio da razão de áreas de modo que, se σ(A) é definido como a “área” do conjunto A, então pode-se definir μ(A) = σ(A) / σ(D).

Problema 1

Dois amigos que levam o metrô para seus trabalhos da mesma estação chegam à estação uniformemente aleatoriamente entre 7 e 7:20 da manhã. Eles estão dispostos a esperar um pelo outro durante 5 minutos, depois dos quais apanham um comboio, juntos ou sozinhos. Qual é a probabilidade do seu encontro na estação?

Num sistema cartesiano de coordenadas (s, t), um quadrado de lado 20 (minutos) representa todas as possibilidades das chegadas matinais dos dois amigos à estação de metro.

A área cinzenta A é delimitada por duas linhas rectas, t = s + 5 e t = s – 5, de modo que dentro de A, |s – t| ≤ 5. Segue-se que os dois amigos só se encontrarão desde que as suas chegadas s e t caiam na região A. A probabilidade de isso acontecer é dada pela razão entre a área de A e a área do quadrado:

/ 400 = 175/400 = 7/16.

Problema 2

(.)

Três pontos A, B, C são colocados aleatoriamente num círculo de raio 1. Qual é a probabilidade de ΔABC ser agudo?.

Ponto Fixo C. As posições dos pontos A e B são então definidas pelos arcos α e β estendendo-se de C em duas direções. A priori sabemos que 0 < α + β < 2π. Os valores favoráveis para os nossos problemas de α e β (como os ângulos agudos subentendidos satisfazem) 0 < α < π e 0 < β < π. Sua soma não poderia ser inferior a π, pois isso tornaria o ângulo C obtuso, portanto, α + β > π. A situação é apresentada no seguinte diagrama onde o quadrado tem o lado 2π.

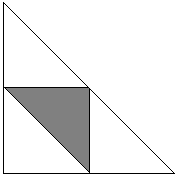
Região D é a intersecção de três meios-planos: 0 < α, 0 < β, e α + β < 2π. Este é o grande triângulo do diagrama acima. Os eventos favoráveis pertencem ao triângulo sombreado que é a intersecção dos meios-planos α < π, β < π, e α + β > π. A proporção das áreas dos dois é obviamente 1/4.

Agora observe, que a menos que o triângulo aleatório seja agudo ele pode ser pensado como obtuso já que a probabilidade de dois dos três pontos A, B, C formarem um diâmetro é 0. (Para BC ser um diâmetro, deve-se ter α + β = π que é uma linha reta, com zero como única atribuição de área possível). Assim, podemos dizer que a probabilidade de ΔABC ser obtuso é de 3/4. Para um triângulo obtuso, o círculo pode ser dividido em duas metades, estando o triângulo inteiramente numa das metades. Segue-se que 3/4 é a resposta à seguinte questão:

Três pontos A, B, C são colocados aleatoriamente sobre um círculo de raio 1. Qual é a probabilidade de que os três se encontrem num semicírculo?

1. E. J. Barbeau, Murray S. Klamkin, W. O. J. Moser, Five Hundred Mathematical Challenges by (MAA, 1995, problema 244.)
2. D. A. Klain, G.-C. Rota Introduction to Geometric Probability , Cambridge University Press, 1997
3. A. A. A. Sveshnikov, Problems in Probability Theory, Mathematical Statistics and Theory of Random Functions, Dover, 1978
4. A. M. Yaglom, I. M. Yaglom, Challenging Mathematical Problems With Elementary Solutions, Dover, 1987

Probabilidade Geométrica

• Probabilidades Geométricas
• A maioria dos triângulos são obtusos?
  • Oito Selecções em Seis Sectores
  • Três Pontos Aleatórios num Círculo
• Probabilidade Geométrica
  • Bastão Partida em Três Peças (Coordenadas Trilineares)
  • Bastão Partida em Três Peças. Solução em Coordenadas Cartesianas
• Paradoxo de Bertrand
• Aves em um Fio (Problema e Simulação Interativa)
  • Aves em um Fio: Solução por Nathan Bowler
  • Pássaros sobre um Fio. Solução por Mark Huber
  • Birds on a Wire: uma simulação probabilística. Solução por Moshe Eliner
  • Pássaros sobre Fio: uma simulação probabilística. Solução por Stuart Anderson
  • Birds on a Wire. Solução por Bogdan Lataianu
• Simulação de Massa de Buffon
• Média de gotas de chuva – um exercício de probabilidade geométrica
  • Média de gotas de chuva, Parte 2
• Rectângulo em um tabuleiro de xadrez: uma Introdução
• Marcação e Quebra de Paus
• Pontos Aleatórios num Segmento
• Cobertura do Semicírculo
• Cobertura do Hemisfério
• Intervalos Aleatórios de Sobreposição
• Intervalos Aleatórios com Um Dominante
• Pontos numa Grelha Quadrada
• Probabilidades Flatas numa Esfera
• Probabilidade em Triângulo

|Contacto|||Página de frente|||Conteúdos||||Conteúdo||||Acima_5667>

Direitos de cópia © 1996-2018 Alexander Bogomolny