O modelo Ising é um exemplo particular de um sistema termodinâmico, e é o sistema modelo para compreender as transições de fase. Sabe quantos biólogos passam tanto tempo com moscas da fruta miseráveis? Bem, os físicos gastam muito tempo com o modelo Ising. Como o Prof. Raghu nos diz, é a Drosophila das transições de fase.

Pessoalmente, eu não sou o maior fã da sua analogia porque eu acho que as moscas da fruta são nojentas. Esperemos que o modelo Ising não seja demasiado nojento.

Motivação

Por que devemos passar tanto tempo a falar do modelo Ising?

• É surpreendentemente útil para nos ajudar a pensar em todo o tipo de comportamentos relacionados com as transições de fase. Por exemplo:

  • o modelo Ising exibe quebra de simetria em fase de baixa temperatura (da qual acabamos de falar)

  • tem um ‘ponto crítico’ especial a uma temperatura bem definida (a que aludimos no diagrama de fases da água)

  • outras características ricas.

• É um dos poucos modelos exactamente solvíveis onde podemos realmente calcular quantidades termodinâmicas e interpretá-las.

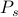  • Em geral, calcular quantidades termodinâmicas é difícil porque temos de resumir muitos termos. Lembre-se da nossa primeira classe térmica que você pode pensar em um sistema de equilíbrio como um conjunto de muitos estados , cada um ponderado com sua própria probabilidade . Neste quadro, as quantidades termodinâmicas que você observa correspondem a médias sobre o conjunto. Em particular, se você quiser encontrar a média do conjunto de alguns observáveis 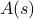, você precisa encontrar a soma 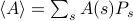, onde a soma corre sobre todos os estados possíveis. O problema com isso, como você se lembra, é que o número de estados de um sistema termodinâmico é escalado exponencialmente com o número de partículas! Mesmo para um sistema de tamanho moderado, há demasiados estados para um computador calcular explicitamente a média – quanto mais um sistema termodinâmico onde 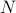está na ordem de .

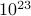  • Então precisamos de “ser espertos” para calcular a função de partição, e devemos estar gratos por sistemas exactamente solvíveis!

• O modelo Ising é simples, mas pode ser aplicado a um número surpreendente de sistemas diferentes.

  • Este é o nosso primeiro gosto de universalidade – uma característica de fenómenos críticos onde a mesma teoria se aplica a todos os tipos de transições de fase diferentes, seja em líquidos e gases ou ímanes ou supercondutores ou o que quer que seja. Os físicos adoram este tipo de comportamento geral porque sugere uma espécie de ordem mais profunda em nosso mundo caótico.

Definição do Modelo Ising

O Modelo Ising é um modelo matemático que não corresponde a um sistema físico real. É uma enorme malha (quadrada) de sites, onde cada site pode estar em um de dois estados. Nós rotulamos cada site com um índice , e chamamos os dois estados e . Para dizer que o ‘o site está no estado , escrevemos .

Agora, esta definição é terrivelmente abstracta e pouco física, por isso para nós, físicos, é extremamente útil ter um sistema real em mente, para que possamos referir-nos a algo explícito e construir a intuição física. Aqui estão alguns sistemas físicos que o modelo Ising pode representar:

• Um íman. Cada site representa um ‘spin’ particular no material (um electrão não emparelhado??), e é se o spin aponta para baixo ou se o spin aponta para cima. Cada um dos giros actua como um mini íman com o seu próprio momento magnético; se todos os giros estiverem alinhados, então toda a malha dos giros comporta-se como um grande íman com um momento magnético macroscópico líquido.

• Uma liga; digamos, latão. Cada um dos locais é um átomo na malha; representa um átomo de cobre nesse local; representa o zinco.

• A ”gás da malha”. Cada um dos locais é a possível localização de uma partícula; significa que o local está vazio e significa que o local está ocupado por uma partícula.

• Treliças de vórtice bacteriano???

Por enquanto, vamos pensar no modelo Ising como um modelo para um íman. É um modelo de íman muito simplificado e de brinquedo, com certeza, mas a analogia do íman pode no entanto ajudar a guiar a nossa querida intuição física.

Conjuntando o Hamiltonian

Uma pergunta natural a fazer sobre este modelo Mickey-mouse de um íman é a energia que ele tem. Para ser mais preciso, queremos escrever uma função que representa a energia de cada uma das configurações possíveis (também conhecida como microestado) dos giros no ímã. Como sabemos, esta função energética é chamada de Hamiltonian.

No modelo Ising, o Hamiltonian inclui dois tipos de interações:

• o termo de campo externo. Como nos lembramos da mecânica quântica, um campo magnético externo pode dividir as energias do estado de spin-down e spin-up, de modo que um é mais alto em energia e o outro é mais baixo.

  • O tamanho de representa o quão forte é o campo, por isso diz-lhe quanto mais alto em energia é um spin do que o outro.

  • O sinal de diz-lhe se é o spin-up ou o spin down que é preferido.

  • Desde que cada spin individual sente o campo externo, temos de somar sobre todos os locais para encontrar a contribuição total para a energia.

• o termo de interação entre os spins vizinhos – talvez eles queiram se alinhar entre si e apontar da mesma maneira, talvez queiram se alinhar e apontar de maneiras diferentes. Fisicamente, podemos imaginar que essa interação surge porque cada giro no ímã é seu próprio mini dipolo magnético que estabelece seu próprio campo magnético, e seus vizinhos podem sentir esse campo magnético.

  • O tamanho de diz-lhe o quanto as giros vizinhas estão acopladas umas às outras – o quanto elas querem (anti-)alinhar. Fisicamente, a força do acoplamento giratório pode depender da distância entre eles na lattica do magneto, por exemplo.

  • O sinal de diz-lhe se os vizinhos preferem alinhar ou anti-alinhar. (O termo técnico para isso é ferromagnético ou anti-ferromagnético, respectivamente). Fisicamente, se um material é um ou outro (ou nenhum dos dois) depende dos detalhes mecânicos quânticos exatos de como os spins interagem.

  • Desde que a interação spin-spin surge entre dois spins, temos de somar sobre pares de locais para encontrar a sua interação total com a energia.

Mais sobre o termo interação

Uma pergunta natural sobre o termo interação spin-spin é quais giros estão acoplados a quais giros?

Se voltarmos à imagem física do íman, e fizermos zoom em alguma rotação em particular, esperamos que a força da interacção spin-spin seja mais forte para as rotações próximas e mais fraca para as rotações longínquas. A exata dependência de distância das interações spin-spin é provavelmente bastante complicada para ímãs reais.

Para o modelo Ising, nós fazemos a suposição mais simples possível para a natureza desta interação spin-spin:

Um pequeno comentário:

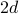• Numa malha quadrada de dimensões , cada local tem vizinhos mais próximos: esquerda e direita numa dimensão, para cima e para baixo depois de adicionar a segunda dimensão, etc…

• Apesamos que a interação é isotrópica – todos os vizinhos são tratados igualmente independentemente da direção.

• Falamos frequentemente das interacções vizinhas mais próximas como a energia de um laço que une dois sítios de grelha.

• Quando estamos somando sobre pares de locais adjacentes, simbolicamente, escrevemos pequenos parênteses em torno dos índices para representar o ”vizinho mais próximo”.

Uma boa consequência das interações vizinho mais próximo é que quando estamos encontrando a energia total de alguma configuração de giros, ao invés de somar sobre todos os pares de locais possíveis, somamos apenas sobre pares de locais que são adjacentes um ao outro.

Agora que discutimos todas estas coisas, estamos prontos para escrever a expressão real para o Hamiltoniano. (Eu queria explicar e interpretar a física antes de escrever o Hamiltoniano para que os símbolos fizessem algum sentido.)

Hamiltoniano do Modelo Ising

O Hamiltoniano do Modelo Ising pode ser escrito como

>

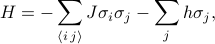
onde reproduz a interação spin-spin, representa o campo externo, e os 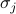são os giros individuais em cada um dos sites da malha. A primeira soma está sobre todos os pares de sites de treliça vizinhos (também conhecidos como links); ela representa as interações entre os spins. A segunda soma está sobre todos os sites da árvore em si; ela representa o campo externo tentando alinhar todas as giros em uma direção.

Continuar com a termodinâmica do modelo Ising.