por Marco Taboga, PhD
A função indicadora de um evento é uma variável aleatória que toma valor 1 quando o evento acontece e valor 0 quando o evento não acontece. As funções indicadoras são frequentemente usadas na teoria da probabilidade para simplificar a notação e para provar teoremas.
Definição
O seguinte é uma definição formal.
Definição Deixar 
ser um espaço de amostra e ser um evento. A função indicadora (ou variável aleatória indicadora) do evento , denotada por , é uma variável aleatória definida da seguinte forma: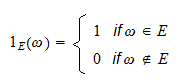
Enquanto o indicador de um evento é normalmente denotado por , por vezes é também denotado por onde é a letra grega Chi.
Exemplo Atiramos um dado e um dos seis números de 1 a 6 pode aparecer virado para cima. O espaço da amostra éDefinir o evento descrito pela frase “Um número par aparece de face para cima”. Uma variável aleatória que toma o valor 1 quando um número par aparece virado para cima e o valor 0 caso contrário é um indicador do evento . A definição caso a caso deste indicador é
Da definição acima, pode-se facilmente ver que é uma variável aleatória discreta com suporte e função massa probabilística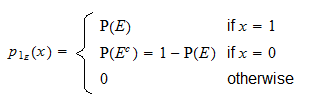
Propriedades
As funções do indicador possuem as seguintes propriedades.
Poderes
A potência – de é igual a : porque pode ser ou ou e
>
Valor esperado
O valor esperado de é igual a :
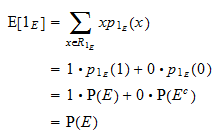
Variância
A variação de é igual a . Graças à fórmula de variância habitual e à propriedade de potência acima, obtemos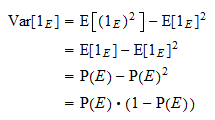
Intersecções
Se e são dois eventos, então causa:
-
se
, então e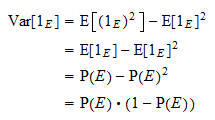
-
se
, então e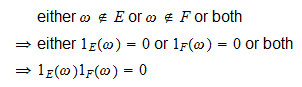
Indicadores de eventos de probabilidade zero
Deixar ser um evento de probabilidade zero e uma variável aleatória integrável. Então,Embora uma prova rigorosa deste fato esteja além do escopo desta exposição introdutória, esta propriedade deve ser intuitiva. A variável aleatória é igual a zero para todos os pontos da amostra excepto possivelmente para os pontos . O valor esperado é uma média ponderada dos valores pode assumir, onde cada valor é ponderado pela sua respectiva probabilidade. Os valores não zero podem assumir são ponderados por probabilidades zero, portanto deve ser zero.
Exercícios resolvidos
Abaixo você pode encontrar alguns exercícios com soluções explicadas.
Exercício 1
Considere uma variável aleatória e outra variável aleatória definida como uma função de .
Expresso usando as funções indicadoras dos eventos e .
Denotar por o indicador do evento e denotar por o indicador do evento . Podemos escrever como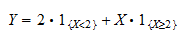
Exercício 2
Que seja uma variável aleatória positiva, ou seja, uma variável aleatória que só pode assumir valores positivos. Vamos ser uma constante. Prove que onde é o indicador do evento .
Primeira nota que a soma dos indicadores e é sempre igual a :Como consequência, podemos escrever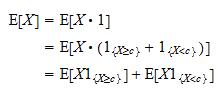
Agora, note que é uma variável aleatória positiva e que o valor esperado de uma variável aleatória positiva é positivo:Assim,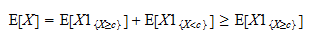
Exercício 3
Que seja um evento e denote a sua função indicadora por . Que seja o complemento de e denote a sua função indicadora por . Você pode expressar em função de ?
A soma dos dois indicadores é sempre igual a :Por isso,
Como citar
Por favor cite como:
Taboga, Marco (2017). “Indicator functions”, Lectures on probability theory and mathematical statistics, Terceira edição. Kindle Direct Publishing. Apêndice online. https://www.statlect.com/fundamentals-of-probability/indicator-functions.