Como calcular a tensão nas cordas que suspendem um objecto
Vemos na ilustração abaixo que a força, F, necessária para levantar o objecto é igual ao peso, W, do objecto. Esta ideia é o conceito fundamental que está subjacente à nossa fórmula de força de tensão. Também é mostrado abaixo o diagrama do corpo livre do objeto que mostra as forças de tensão, T, atuando na corda. Como você pode ver, as forças de tensão vêm em pares e em direções opostas:
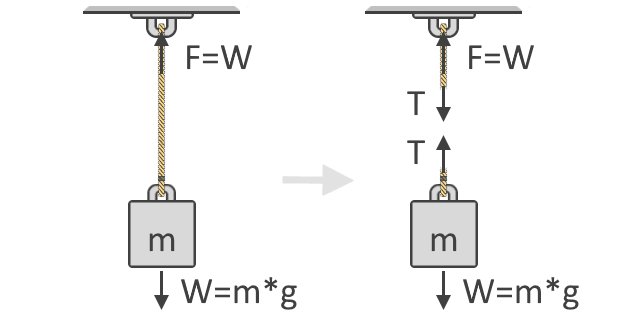
Segundo a Segunda Lei do Movimento de Newton, podemos então expressar a soma das forças usando o diagrama de corpo livre do objeto, como mostrado no lado direito da ilustração acima. Nós usamos diagramas de corpo livre para mostrar as diferentes direções e magnitudes das forças que atuam sobre um corpo. Em equilíbrio, todas estas forças devem ser iguais a zero. Considerando todas as forças para cima como positivas e para baixo como negativas, nossa equação é:
ΣF = 0 = T + (-W)T = W
onde o peso, W, se torna negativo já que é dirigido para baixo. Ao transpor W para o outro lado da equação, podemos agora ver que a força de tensão na corda é igual ao peso do objeto que ela carrega, como também mostrado acima.
Se usarmos mais cordas para levantar o objeto, a força total de tensão se divide nas cordas. A força de tensão em cada corda depende de seus ângulos em relação à direção da força a que ela se opõe. Para compreender melhor isto, consideremos outro diagrama de corpo livre de um objeto suspenso por duas cordas, como mostrado abaixo:
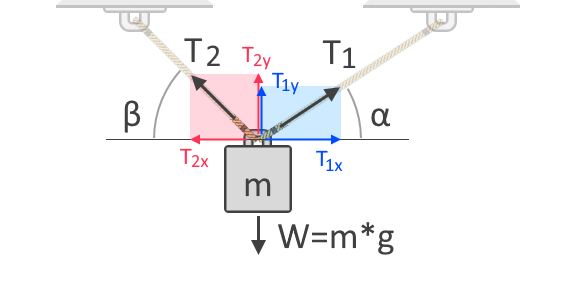
No diagrama de corpo livre mostrado acima, podemos ver os componentes horizontal e vertical das forças de tensão, T₁, e T₂. As forças são vetores, o que significa que elas sempre têm tanto magnitudes quanto direções. Como todos os vetores, as forças podem ser expressas nestes componentes, o que dá a influência da força ao longo dos eixos horizontal e vertical. T₁ₓ e T₂ₓ são os componentes verticais de T₁ e T₂, respectivamente. Por outro lado, T₁ᵧ e T₂ᵧ são os componentes verticais das mesmas forças, respectivamente. Como a gravidade atua sobre o objeto no eixo vertical, precisamos considerar os componentes verticais das forças de tensão para a nossa soma de forças da seguinte forma:
ΣF = 0 = T₁ᵧ + T₂ᵧ + (-W)W = T₁ᵧ + T₂ᵧ
Porque também conhecemos os ângulos das forças de tensão, podemos expressar T₁ᵧ e T₂ᵧ em termos de T₁ e T₂, respectivamente, com a ajuda de funções trigonométricas:
T₁ᵧ = T₁ * sin(α)T₂ᵧ = T₂ * sin(β)W = T₁ * sin(α) + T₂ * sin(β)
>
Podemos também dizer que para que o sistema esteja em equilíbrio, o objecto não deve mover-se horizontalmente ou ao longo do eixo x. Portanto, os componentes horizontais de T₁ e T₂ devem então ser iguais a zero. Também, com a ajuda da trigonometria, podemos expressar T₁ₓ e T₂ₓ em termos de T₁ e T₂, respectivamente:
T₁ₓ = T₂ₓT₁ * cos(α) = T₂ * cos(β)
Se dividirmos ambos os lados por cos(α), obtemos uma equação em que T₁ é expressa em termos de T₂ e dos ângulos:
T₁ = T₂ * cos(β) / cos(α)
Podemos então usar esta equação para resolver para T₂ substituindo T₂ * cos(β) / cos(α) como o T₁ na nossa equação de soma de forças, como mostrado abaixo:
W = T₁ * sin(α) + T₂ * sin(β)W = T₂ * * sin(α) + T₂ * sin(β)W = T₂ * T₂ = W /
Finalmente, se multiplicarmos toda esta equação por cos(β) / cos(α) como derivamos no valor de T₁ em termos de T₂, e depois simplificando tudo, obtemos esta equação:
T₁ = W / * T₁ = W / * T₁ = W /
Agora tudo o que você precisa saber são os ângulos das cordas de tensão em relação à horizontal. Se for dado um ângulo em relação à vertical, basta subtrair este ângulo de 90°. Fazendo isso, você obterá o ângulo a partir da horizontal. No entanto, se lhe forem dados outros valores de ângulos que possam ser superiores a 90° ou mesmo 180°, talvez queira verificar a nossa calculadora de ângulos de referência para o ajudar a determinar o ângulo de que necessita. Depois de determinar os valores das variáveis nas nossas fórmulas de força de tensão, podemos agora resolver para as forças de tensão.