Como a luz reflete ou transmite a partir de uma estrutura material, há uma mudança na polarização. A elipsometria mede esta resposta que depende das propriedades ópticas e da espessura dos materiais individuais. A elipsometria é usada principalmente para determinar constantes ópticas e espessura do filme, mas também para caracterizar composição, cristalinidade, rugosidade, concentração de doping e outras propriedades do material associadas a uma mudança na resposta óptica.

As áreas de aplicação são pesquisas básicas em ciências físicas, soluções de semicondutores e armazenamento de dados, telas planas, comunicação, biosensores e indústrias de revestimento óptico. A elipsometria também tem a flexibilidade de medir a maioria dos tipos de materiais: dielétricos, semicondutores, metais, supercondutores, orgânicos, revestimentos biológicos e compósitos.

Definição de luz polarizada

A luz pode ser descrita como uma onda eletromagnética que viaja através do espaço. A forma como o campo de uma onda eletromagnética se comporta em relação ao espaço e ao tempo é referida como polarização. A luz é considerada como não polarizada quando a sua orientação e fase são totalmente arbitrárias. A elipsometria, entretanto, mede a luz polarizada – um campo elétrico que segue um caminho específico e tem uma forma distinta em qualquer ponto dado. Uma onda electromagnética que viaja em direcção z pode ser descrita pelos seus componentes x e y, porque o seu campo eléctrico é sempre ortogonal à direcção de propagação. Quando duas ondas de luz ortogonais estão em fase, a luz resultante é linearmente polarizada. A sua orientação é determinada pelas amplitudes relativas. A luz é considerada circularmente polarizada se as ondas ortogonais estiverem 90° fora de fase e tiverem a mesma amplitude. A polarização mais comum é a elíptica e combina ondas ortogonais de amplitude e fase arbitrárias. É aqui que a elipsometria recebe o seu nome.

Diferentes tipos de polarização:

Linear

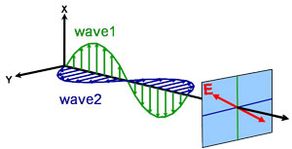
Circular

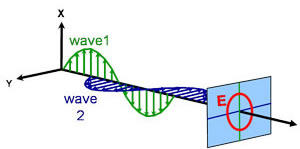
Elíptica

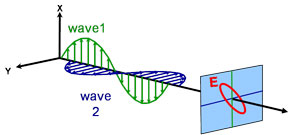
Propriedades ópticas

As propriedades ópticas que determinam como a luz interage com um material são descritas por dois valores. Elas são geralmente representadas como um número complexo. O índice de refração complexo (ñ) consiste no índice (n) e um coeficiente de extinção (k):

As propriedades ópticas também podem ser representadas como uma função dielétrica complexa:

com a seguinte relação entre as convenções:

O índice representa a velocidade de fase da luz quando se viaja num material em comparação com a velocidade da luz quando se viaja no vácuo, c:

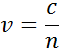
Quando se entra num material com um índice mais elevado, a luz abranda. Como a frequência das ondas de luz não muda, o comprimento de onda encurta. A perda de energia das ondas para o material é descrita pelo coeficiente de extinção que está relacionado com o coeficiente de absorção da seguinte forma:

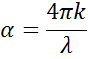
De acordo com a Lei da Cerveja, a luz perde intensidade em um material absorvente. O coeficiente de extinção demonstra como a luz desaparece rapidamente num material.

>

Figure 4 mostra uma onda de luz viajando através de dois materiais diferentes de propriedades variáveis antes de retornar ao ambiente.

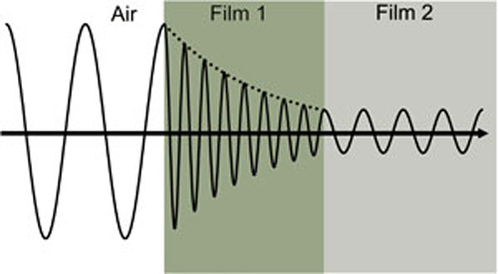
Figure 4: Onda de luz viajando do ar para a película absorvente 1 e depois película transparente 2. Velocidade de fase e variação do comprimento de onda em ambos os materiais dependendo do índice de refração (Filme 1: n=4, Filme 2: n=2).

O comprimento de onda determina as constantes ópticas. A Figura 5 mostra as constantes ópticas para o TiO2 do UV ao IR. Devido aos diferentes processos que retiram energia da onda de luz, a absorção (k>0) ocorre tanto no UV como no IR. A absorção de IV é geralmente causada por vibração molecular ou fonónica ou por transportadores livres. A absorção de UV geralmente ocorre devido às transições eletrônicas, onde a energia da luz excita os elétrons para estados elevados. A Figura 5 mostra que as constantes ópticas hipotéticas ou reais não são independentes, mas ligadas matematicamente através das relações Kramers-Kronig.

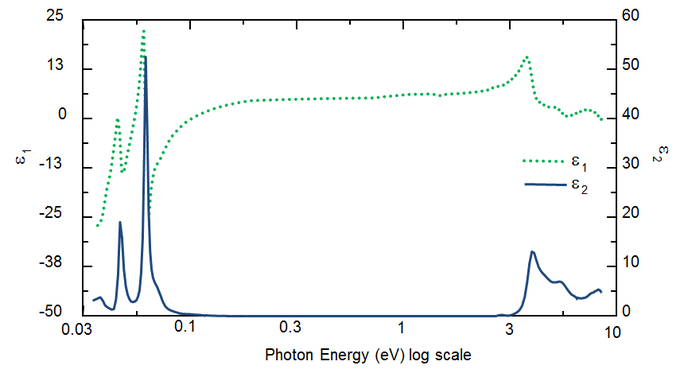
Figure 5: Função dielétrica complexa para filme de TiO2 com comprimentos de onda de IR (eV pequeno) a UV (eV alto).

Interacção entre luz e materiais

Quando a luz interage com um material isto leva a condições de contorno na interface. Durante isto, as equações de Maxwell devem permanecer sempre satisfeitas. A figura abaixo mostra como a luz incidente reflete e refracta na interface. O ângulo entre o raio incidente e a amostra normal (θi) será igual ao ângulo refletido (θr). A luz que entra num material é refracta num ângulo θt dado por:

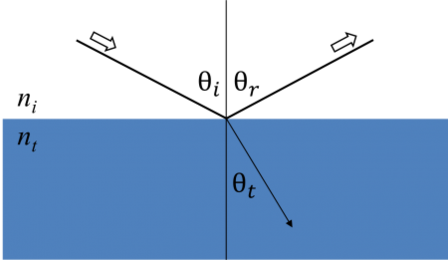
Figure 6: A luz reflecte e refracta de acordo com a lei de Snell.

Em cada interface uma porção de luz é reflectida enquanto o resto transmite no ângulo refractado. Dependendo das condições de contorno, aplicam-se diferentes soluções para campos elétricos paralelos e perpendiculares à superfície da amostra. Assim, a luz pode ser separada em componentes ortogonais em relação ao plano de incidência (p- e s-polarizado). Ambos os componentes podem ser calculados separadamente. Assim, Fresnel descreveu a quantidade de luz refletida e transmitida em uma interface entre materiais:

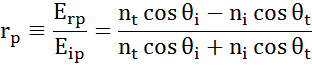
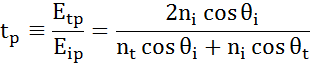
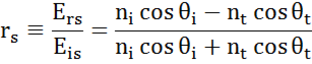
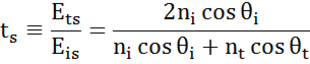
Interfaces múltiplas com coeficientes de reflexão e transmissão Fresnel apropriados ocorrem com filme fino e estruturas multicamadas. Para definir corretamente o feixe refletido ou transmitido, a fase relativa de cada componente de luz deve ser rastreada. A espessura da fase do filme é assim determinada da seguinte forma:

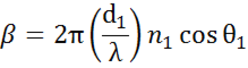
Quando várias ondas de luz se sobrepõem, ocorre interferência que depende da fase relativa de cada onda de luz individual. A figura abaixo mostra a combinação de ondas de luz no feixe refletido e seus correspondentes cálculos Fresnel.

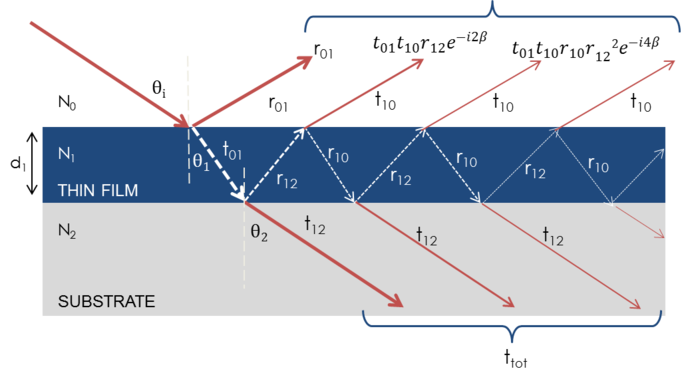
Figure 7: A luz reflete e refracta em cada interface individual, o que leva a múltiplos feixes em uma película fina. A interferência dos feixes depende da fase relativa e da amplitude dos campos elétricos. A reação dos feixes pode ser calculada com coeficientes de reflexão e transmissão Fresnel.

Medições

Ellipsometria mede principalmente como p- e s-componentes reagem em relação um ao outro durante a reflexão ou transmissão. Assim, um feixe de referência é sempre parte da experiência. Uma polarização conhecida é refletida ou transmitida a partir da amostra e a polarização de saída é medida. A alteração da polarização é a medida da elipsometria:

Figure 6 mostra uma medida típica da elipsometria da amostra. A luz incidente linear tem componentes p- e s-. A luz reflectida mostra tanto a amplitude como as mudanças de fase da luz polarizada p- e s-. Estas mudanças são medidas pela elipsometria.

Para recolher dados da elipsometria é necessário o seguinte: fonte de luz, gerador de polarização, amostra, analisador de polarização e detector. Tanto o gerador de polarização como o analisador são feitos de partes ópticas que manipulam a polarização: compensadores, polarizadores e moduladores de fase. As configurações típicas de elipsômetros incorporam analisador rotativo (RAE), polarizador rotativo (RPE), compensador rotativo (RCE), e modulação de fase (PME). A figura abaixo mostra uma configuração RAE.

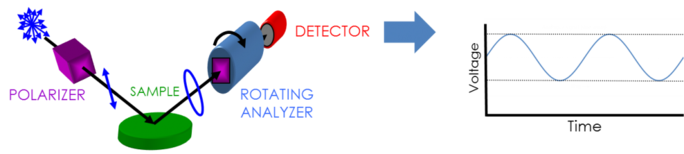
A luz não polarizada é produzida por uma fonte de luz e depois enviada através de um polarizador. O polarizador é configurado para permitir a passagem somente de luz com uma certa orientação de campo elétrico. Como o eixo do polarizador está alinhado entre os planos p- e s-, ambos atingem a superfície da amostra. A luz agora linearmente polarizada é refletida da superfície da amostra, tornando-se assim elipticamente polarizada, e então enviada através de um polarizador de rotação contínua (o “analisador”). A quantidade de luz que é permitida passar depende da orientação do polarizador em relação à elipse do campo elétrico da amostra. Para definir a polarização refletida, a luz é convertida em um sinal eletrônico no detector. A comparação destes dados com a polarização de entrada estabelecida fornece informação sobre a alteração causada pela reflexão da amostra: a medição elipsométrica de Psi e Delta.

Análise de dados

Ellipsometria é utilizada para definir a espessura do filme de material ou constantes ópticas através da medição das alterações na polarização da luz. Constantes ópticas “Pseudo” da medição da elipsometria podem ser derivadas invertendo os dados determinados para uma única reflexão. Isto é útil para material a granel.

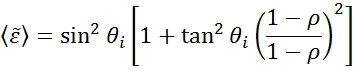
A equação acima não conta com nenhuma camada superficial. No entanto, normalmente há um óxido de superfície ou rugosidade nos materiais a granel. Uma inversão direta incluirá estes dados como parte das constantes ópticas a granel. Veja a fig. 10 para uma visão geral de um processo típico de análise de dados usado em medições de elipsometria. Uma vez que uma equação exata não pode ser escrita, uma análise de regressão é necessária. A resposta é frequentemente superdeterminada com apenas algumas incógnitas e centenas de pontos de dados experimentais. Uma análise de regressão permite que todos os dados medidos sejam incluídos ao determinar a solução.

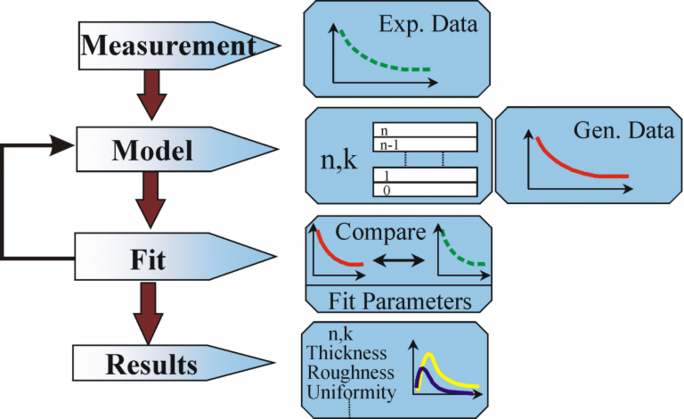
Figure 10: Fluxograma para análise de dados de elipsometria.

O seguinte procedimento é usado para análise de dados: a amostra é medida e um modelo é feito da amostra. Com a ajuda deste modelo são calculados os resultados assumidos a partir das equações de Fresnel, que descrevem a espessura e as constantes ópticas de cada material. É feita uma avaliação do cálculo preliminar, caso esses valores sejam desconhecidos. Os valores calculados são comparados com os dados experimentais. Para melhor corresponder aos dados experimentais e de cálculo, os dados de materiais desconhecidos podem ser variados. Entretanto, os pontos de dados experimentais devem ser sempre mais do que os parâmetros desconhecidos. Por exemplo, no máximo duas propriedades do material podem ser determinadas com um elipsômetro de um comprimento de onda, pois ele produz exatamente dois pontos de dados: Ψ, Δ (Psi e Delta). A regressão é usada para encontrar a melhor combinação entre modelo e experimento. A diferença entre as curvas de dados é quantificada com a ajuda de um estimador como o erro médio quadrático (MSE). As propriedades desconhecidas são variadas até que o MSE mínimo seja alcançado. Isto significa que o menor MSE é equivalente à melhor resposta.

Ver a figura abaixo para a curva MSE versus a espessura do filme para um filme transparente sobre silício. O menor valor de MSE ocorre a uma espessura de 749 nm, apesar de um número de mínimos locais. Assim, a espessura correta do filme também é de 749 nm. O algoritmo de regressão pode considerar um mínimo local para ser correto. Assim, para determinar o mínimo global correto é sábio comparar os resultados por olho para o MSE mais baixo.

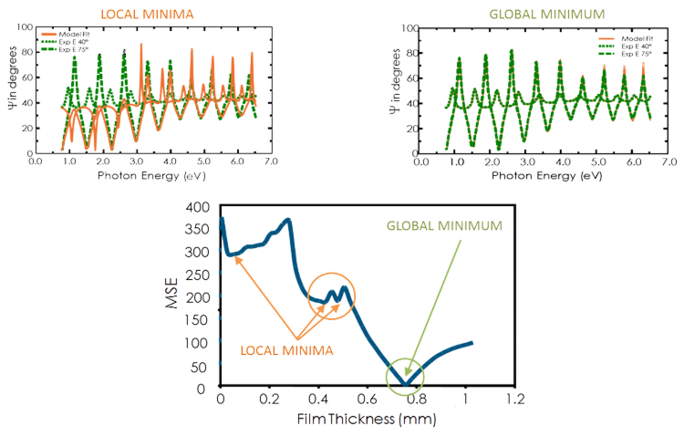
Figure 11, top-direita: Dados experimentais e curvas correspondentes geradas para o modelo no mínimo global. Figura 11, superior-esquerda: Uma curva similar no mínimo local perto de uma espessura de 0,45 µm pode ser facilmente identificada como resultado incorreto. Figura 11, inferior: A curva MSE versus a espessura mostra o mínimo global. Um algoritmo de regressão pode dar mínimos locais, mas não o resultado final.

Determinar a espessura do filme

A espessura do filme é normalmente determinada pela interferência entre a luz que reflete da superfície e a luz que viaja através do filme. Se essa interferência é considerada construtiva ou destrutiva depende da fase relativa da luz que se junta à reflexão superficial. A interferência inclui tanto a amplitude como as informações de fase. A informação de fase de Δ é muito sensível a filmes até à espessura da sub-camada. Veja a figura abaixo para uma comparação da intensidade refletida e elipsometria para a mesma série de camadas finas de SiO2 sobre Si. A reflectância para cada película é quase a mesma enquanto que existem grandes variações em Δ.

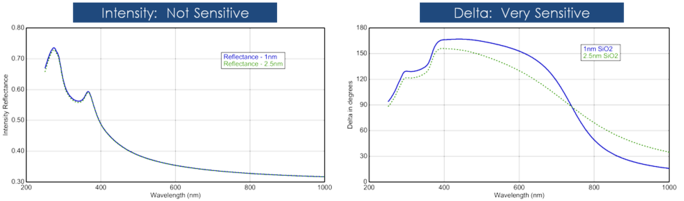
Figure 12, à esquerda: Intensidade refletida e delta elipsométrica (direita) para dois óxidos finos sobre silício. A medida da intensidade não mostra que o Delta é altamente sensível a filmes de escala nanométrica.

Ellipsometria é comumente usada para filmes desde sub-nanômetros até alguns micrômetros de espessura. Com películas de espessura superior a várias dezenas de mícrons, as oscilações de interferência só podem ser resolvidas com dificuldade crescente, exceto quando são utilizados comprimentos de onda infravermelhos mais longos. É por isso que para filmes mais espessos são normalmente usadas outras técnicas de medição.

Para medir a espessura, uma porção da luz tem que viajar através do filme completo e depois retornar à superfície. Com materiais absorventes de luz, as medições da espessura óptica só podem ser realizadas em camadas finas e semi-opacas, a menos que sejam realizadas em regiões espectrais com menor absorção. Por exemplo, uma película orgânica que absorve a luz UV e IV pode ser transparente em comprimentos de onda médios visíveis. Os metais absorvem fortemente em todos os comprimentos de onda, por isso a espessura máxima da camada que pode ser determinada situa-se em torno de 100 nm.

Constantes Ópticas

Constantes Ópticas desempenham um papel importante nas medições de espessura. A espessura de um filme influencia o comprimento do percurso da luz que percorre o filme, o índice determina a velocidade da onda de luz e o ângulo refractário. Ambos contribuem, portanto, para o atraso entre a luz que percorre o filme e a reflexão superficial. É necessário estabelecer n e k assim como a espessura para obter resultados corretos de uma medição óptica.

Como as constantes ópticas de um material variam para diferentes comprimentos de onda, todos os comprimentos de onda que são analisados com o elipsômetro devem ser determinados individualmente. A resposta de um material em cada comprimento de onda pode ser antecipada usando uma tabela de constantes ópticas. Para evitar o ajuste cuidadoso de constantes ópticas desconhecidas comprimento de onda por comprimento de onda, é favorável o uso simultâneo de todos os comprimentos de onda. Os parâmetros ajustáveis de uma relação de dispersão, por exemplo, permitem que a forma geral da constante óptica corresponda aos resultados experimentais. Em comparação com o ajuste individual dos valores n e k para cada comprimento de onda, o número de parâmetros livres desconhecidos é reduzido consideravelmente.

As relações Cauchy ou Sellmeier são frequentemente utilizadas para descrever o índice para materiais transparentes onde a relação Cauchy é normalmente dada como:

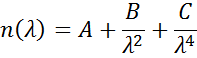
com os três termos ajustados para corresponder ao índice de refracção do material. A relação Cauchy não é limitada pela consistência Kramers-Kronig (KK) e pode levar a uma dispersão não física. A relação Sellmeier, por outro lado, impõe a consistência Kramers-Kronig (KK), que assegura que a dispersão óptica mantenha uma forma realista. A relação Sellmeier é tipicamente escrita como:

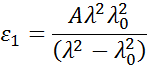
Absorbing materials frequentemente têm uma região de comprimento de onda transparente que pode ser modelada com a relação Cauchy ou Sellmeier. Enquanto a região absorvente, no entanto, deve ser responsável tanto por constantes ópticas reais como imaginárias. Para descrever a absorção de vários materiais, muitas relações de dispersão utilizam a teoria dos osciladores, incluindo Lorentz, Harmonic, e Gauss. Todos eles compartilham atributos semelhantes com as características de absorção sendo descritas com Amplitude, Ampliação e Energia Central (relacionada à freqüência da luz). A forma do componente real é calculada usando a consistência de Kramers-Kronig após o comportamento imaginário ser descrito pelo oscilador. Para incluir a possível absorção extra na região espectral medida, é adicionado um deslocamento para o componente real. O oscilador de Lorentz pode ser escrito como:

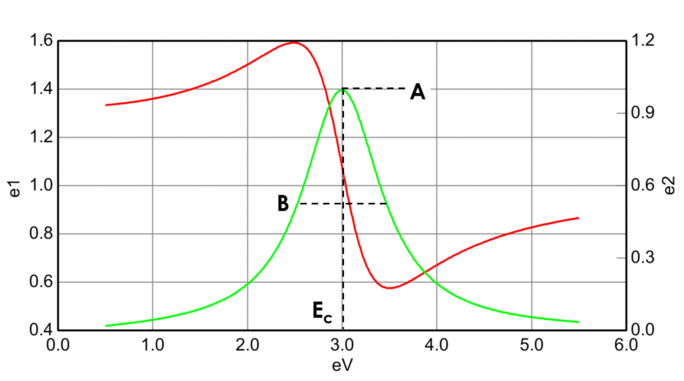
Figure 13 também mostra Amplitude (A), Ampliação (B), Energia Central (Ec) e offset (e1, off set) para um oscilador típico de Lorentz. A energia E está relacionada com a freqüência de uma onda, n:

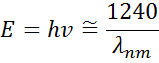
A constante h do Planck e o comprimento de onda λ são dados em nanômetros. Outros modelos de dispersão, como Tauc-Lorentz e Cody-Lorentz, incorporam termos para descrever a energia do bandgap.

Outras Leituras

Ellipsometria é uma técnica óptica estabelecida para a medição de filmes finos e materiais a granel. Ela usa as mudanças de polarização causadas pela reflexão/transmissão de uma estrutura material para determinar as características do material como espessura e constantes ópticas.

Aspnes D.E. (1985). A determinação precisa das propriedades ópticas por elipsometria. In: Palik E.D. (ed.) Handbook of Optical Constants of Solids, pp. 89-112. Academic Press, Orlando.

Azzam R.M.A. e Bashara N.M. (1987). Ellipsometry and Polarized Light, Elsevier Science B.V., Amsterdam, The Netherlands.

Boccara A.C., Pickering C., e Rivory J. (eds.), (1993). Spectroscopic Ellipsometry, Elsevier Publishing, Amsterdam.

Collins R.W., Aspnes D.E., e Irene E.A. (eds.), (1998). “Proceedings from the Second International Conference on Spectroscopic ellipsometry”. In: Thin Solid Films, vols. 313-314.

Fujiwara H., Spectroscopic Ellipsometry, Principles and Applications, John Wiley & Sons, Ltd. 2007

Gottesfeld S., Kim Y.T., e Redondo A. (1995). “Recent applications of ellipsometry and spectroellipsometry in electrochemical systems”, In: I. Rubinstein (ed.), Physical Electrochemistry: Principles, Methods, and Applications, Marcel Dekker, New York.

Herman, I.P. (1996). Optical Diagnostics for Thin Film Processing, pp 425-479. Academic Press, San Diego, Califórnia.

Johs B. et al (1999). “Overview of Variable Angle Spectroscopic Ellipsometry (VASE), Part II: Advanced Applications” (Visão Geral da Elipsometria Espectroscópica de Ângulo Variável (VASE), Parte II: Aplicações Avançadas). Optical Metrology, vol. CR72, pp 29-58. SPIE, Bellingham, Washington.

Johs B. et al (2001). “Recent Developments in Spectroscopic Ellipsometry for in situ Applications”. In: Duparré A, Singh B (ed.) Optical Metrology Roadmap for the Semiconductor, Optical, and Data Storage Industries II, vol. 4449, pp 41-57. SPIE, Bellingham, Washington.

Roseler A. (1990). Infrared Spectroscopic Ellipsometry, Akademie-Verlag, Berlin.

Rossow U. e Richter W. (1996). “Elipsometria Espectroscópica” in: Bauer G e Richter W. (eds.) Optical Characterization of Epitaxial Semiconductor Layers, pp. 68-128, Springer-Verlag, Berlin.

Tompkins H.G. (1993). A User’s Guide to Ellipsometry, Academic Press, San Diego, California.

Tompkins H.G. and McGahan W.A. (1999). Spectroscopic Ellipsometry and Reflectometry, John Wiley & Sons, Inc., USA.

Tompkins, H. G. e Irene E.A. (eds.), 2005, Handbook of Ellipsometry, William Andrew Publishing, New York.

Tompkins, H. G. e Hilfiker, J. H., Spectroscopic Ellipsometry, Practical Application to Thin Film Characterization, 2016, Momentum Press Engineering

Woollam J.A. e Snyder P.G. (1992). “Elipsometria Espectroscópica de Ângulo Variável” in: Brundle CR, Evans CA, e Wilson S (eds) Encyclopedia of Materials Characterization: Surfaces, Interfaces, Thin Films, pp. 401-411, Butterworth-Heinemann, Boston.

Woollam J.A. et al (1999). “Overview of Variable Angle Spectroscopic Ellipsometry (VASE), Part I: Basic Theory and Typical Applications” (Visão Geral da Elipsometria Espectroscópica de Ângulo Variável (VASE), Parte I: Teoria Básica e Aplicações Típicas). Optical Metrology, vol. CR72, pp 3-28. SPIE, Bellingham, Washington.

Woollam J.A. (2000). “Elipsometria, espectroscopia de ângulo variável” in: Webster J.G. (ed.) Wiley Encyclopedia of Electrical and Electronics Engineering, pp. 109-116. John Wiley & Sons, New York.