Zero é um número que cai diretamente entre os números positivos e negativos da linha numérica. Zero é considerado um número inteiro, juntamente com os números naturais positivos (1, 2, 3, 4…) e os números negativos, (…-4,-3,-2,-1).

Zero é um número especial nos números inteiros, pois é o único número inteiro que não é nem positivo nem negativo. É também o único número inteiro que não é um número principal nem um número composto. É considerado um número par porque é divisível por 2, sem nenhum resto. Zero é o elemento de identidade aditivo em vários sistemas de álgebra, e o dígito “0” é usado como um valor de espaço em sistemas de notação posicional para representar números.

Zero tem muitas propriedades interessantes que o tornam de interesse para os matemáticos. Se você adicionar ou subtrair zero de qualquer número, o número permanece o mesmo Se você multiplicar 0 por qualquer número, o resultado é 0. Qualquer número elevado à potência zeroth (0th) é 1, portanto 20=1 e 560=1. Na álgebra tradicional, a divisão por 0 é indefinida, portanto nenhum número pode ser dividido por 0. O número 0 é também um elemento dos números reais e números complexos.

História do Número 0

De onde veio a ideia do zero? Hoje em dia, parece-nos intuitivo; zero é um número que representa uma quantidade nula – um nada. Vemos zeros em toda a sociedade, e naturalmente entendemos o que significam e como podem ser manipulados matematicamente. Historicamente, porém, o conceito de 0 levou algum tempo para ser universalmente reconhecido como um objeto da matemática, e muitos ao longo da história argumentaram que o número zero não existe, ou que a idéia zero é um conceito incoerente.

Muitas sociedades antigas não tinham um conceito explícito da quantidade de zero ou um dígito específico para usar para sua representação. Tanto os antigos egípcios como os babilônios tinham alguma idéia de uma quantidade nula e uma necessidade de valores placeholders na representação de números, mas nunca desenvolveram um dígito ou conceito distinto para representar essa quantidade ou valor placeholder. Os antigos sistemas de numeração egípcios eram inteiramente pictóricos e não tinham valores posicionais, enquanto os antigos babilônios usavam espaços entre números para representar valores posicionais.

Os maias tinham um conceito explícito de 0 e tinham um dígito distinto para representar o conceito e usar como um valor placeholder em seu sistema de calendário vigesimal (base-20). Enquanto os Maias, Olmec e outras sociedades pré-colombianas estavam entre as primeiras na história a ter uma compreensão explícita e sofisticada do número 0, estes sistemas não influenciaram as sociedades do Velho Mundo na Europa.

Os Gregos Antigos, por outro lado, tinham uma relação complicada com o zero. Eles não tinham um símbolo para o seu conceito ou para ele como um valor de lugar reservado, pois não tinham certeza se o número 0 poderia ser considerado uma coisa existente genuína. Como, perguntaram eles, poderia algo (um número) não ser nada (zero)? Para os gregos, os números naturais (1, 2, 3, 4,…) foram derivados do nosso entendimento de objetos individuais discretos no mundo. O próprio Aristóteles argumentou que 0 não existe, com o argumento de que 0 representa um vazio ou nada, e um vazio ou nada genuíno não pode existir.

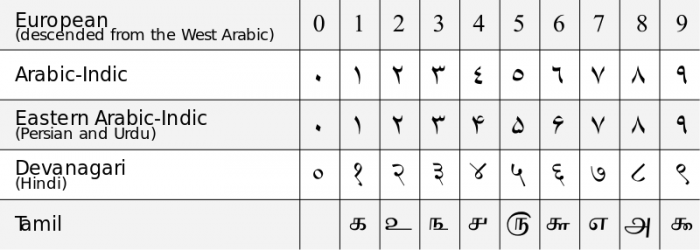
Os chineses tinham um entendimento de “0” como um dígito de espaço reservado para seus sistemas de contagem, mas eles não consideravam o dígito “0” para representar qualquer número distinto, apenas um símbolo útil. O entendimento comum de 0 como um número distinto e como um dígito para sistemas de notação posicional veio da Índia durante o século VI dC. Os matemáticos indianos da época desenvolveram os primeiros tipos de sistemas de notação decimal (base-10) que incorporavam 0 como um dígito distinto e tinham uma compreensão das propriedades matemáticas únicas do zero. No século XI dC, a ideia do zero tinha-se espalhado pela Europa Ocidental através da influência dos matemáticos islâmicos que viviam em Espanha sob o califado Umayyad, e foi criado o sistema de numeração árabe moderno de notação decimal. O primeiro uso da palavra inglesa “zero” data de 1589.

Propriedades Matemáticas do Zero

O número zero desempenha um papel integral em quase todos os campos da matemática. Zero é o menor número inteiro não-negativo e não tem número natural procedente dele. Como 0 é um número inteiro, é também um número racional, um número real, e um número complexo. Em matemática, 0 é considerado uma quantidade que corresponde a uma quantidade nula. Pode-se dizer que zero é a “quantidade” possuída por um conjunto que não tem membros.

Em Álgebra

Em Álgebra elementar, o zero é frequentemente expresso como estando no centro da linha numérica. O número 0 é considerado um número par, pois é um múltiplo inteiro do número 2 (2×0=0). 0 não é um número primo porque tem uma quantidade infinita de fatores, e não é um número composto porque nenhum produto de dois números primos é igual ao número 0.

Com respeito aos 4 operadores aritméticos principais (+, -, ×, ÷) e à operação exponente, o número 0 comporta-se de acordo com as seguintes regras:

• Adição: x+0=0+x=x. Zero é considerado o elemento de identidade aditivo como qualquer número mais ou menos zero é igual a esse número
• Subtração: x-0=x e 0-x=-x
• Multiplicação: x⋅0=0⋅x=0. Qualquer número vezes 0 também é igual a 0,
• Divisão: 0/x=0, exceto quando x=0. x/0 é uma quantidade matematicamente indefinida, já que 0 não tem inverso multiplicativo (nenhum número vezes 0 dá 1).
• Exponentes: x0=1, exceto quando x=0. Há muito tempo se discute se 00 é indefinido ou uma expressão bem formada. Para todos os positivos x, 0x=0,

Em expressões envolvendo limites, a quantidade 0/0 pode aparecer no contexto da demonstração de limites de funções racionais como f(x)/g(x). Nesses casos, 0/0 não é indefinido, mas representa uma forma indeterminada. Isto não significa que o limite é indefinido mas que tem de ser calculado através de outro método, tal como encontrar derivadas. Existem alguns modelos algébricos onde a divisão por zero dá uma quantidade definida, como a linha real estendida projetivamente ou a esfera de Riemann.

Na teoria do conjunto

Na teoria do conjunto, o número 0 corresponde à cardinalidade do “conjunto vazio” ou do “conjunto nulo” (comumente representado como {} ou {∅}. A cardinalidade de um conjunto é a quantidade de elementos desse conjunto se não se tiver laranjas, então tem-se um conjunto de 0 laranjas (um conjunto vazio de laranjas).

Zero é frequentemente usado como ponto de partida na teoria do conjunto para construir o resto dos números naturais. Estas construções von Neumman, com o nome do famoso polimaturgo John von Neumann constrói os números naturais definindo 0={} e define uma função sucessora S(a) = a ∪ {a}. A totalidade dos números naturais pode ser construída a partir das aplicações recursivas da função sucessora, começando com o conjunto vazio:

0 = {}

1 = 0 ∪ {0} = {0} = {{{}}

2 = 1 ∪ {1} = {0,1} = {{{}, {{}}

3 = 2 ∪ {2} = {0, 1, 2} = {{{}, {{{}}, {{{}}, {{{{}}}}

e assim por diante. Seguindo este padrão, pode-se construir todo o conjunto infinito dos números naturais. Desta forma, podemos dizer que cada número natural corresponde ao conjunto contendo todos os números naturais antes dele.

Em Física

No contexto da realização de medições quantitativas em física, 0 é considerado como a linha de base a partir da qual todas as outras medições de unidades são feitas. Muito frequentemente, a linha de base de 0 corresponde a alguma variável fisicamente significativa que é naturalmente distinguível de todas as outras grandezas de medida.

Por exemplo, na escala de Kelvin, uma temperatura de 0 K corresponde ao 0 absoluto – a temperatura mais fria que é fisicamente possível. Na escala de temperatura Celsius, 0 °C é definido como o ponto de congelamento da água a pressões atmosféricas. No contexto da dinâmica e do eletromagnetismo, um valor de 0 é dado à posição na qual um sistema tem a mínima quantidade possível de energia potencial. Por exemplo, ao estado do solo de um átomo, o nível de energia mais baixo possível para os electrões no átomo, é frequentemente atribuído um valor de 0,

Likewise, no contexto da cinemática, o quadro de referência a partir do qual são feitas as observações de movimento é definido como tendo um ponto central colocado na origem do eixo de coordenadas no ponto (0, 0). No caso de quantidades conservadas, como energia de massa, momento e momento angular, a quantidade total de mudança para quantidades conservadas num sistema isolado é sempre igual a 0,

Na Informática

Os computadores armazenam informação sob a forma de sequências bits-longas de 1s e 0s. Nesta representação binária, 0 corresponde a uma posição “off” e é contrastado com a posição “on” designada por 1. Um valor de 0 num circuito eléctrico significa que o circuito está desligado e não tem qualquer fluxo eléctrico. Da mesma forma, muitas lógicas computacionais definem “0” como sendo o caracter que representa um falso valor de verdade.

Em bancos de dados de computador, os elementos de um array são contados usando um sistema de contagem baseado em zero. Isto significa que para um conjunto com n elementos, os elementos têm índices começando com 0. Assim, um elemento com um número índice de 0 é na verdade o primeiro elemento da série, e um número índice de 1 corresponde ao segundo elemento, e assim por diante. Em geral, o enésimo termo de um conjunto tem um número de índice correspondente a n-1. Este sistema de contagem pode causar confusão a novos programadores que estão acostumados a atribuir intuitivamente valores de índice começando com 1,