Ile wiesz o nieskończoności? Prawdopodobnie słyszałeś o liczbie, która jest największą możliwą liczbą lub niemożliwie dużą.
Aby wyjaśnić nieskończoność, muszę najpierw zdefiniować pewną terminologię.
Całkowitości to liczby używane do liczenia. Zbiór liczb całkowitych jest zdefiniowany jako wszystkie liczby bez składników ułamkowych. Niektóre przykłady to: -12, 0, 1, 3, 42, 17.
Nieskończoność to pojęcie obiektu znajdującego się poza zasięgiem liczb naturalnych. Został on po raz pierwszy skonceptualizowany przez rosyjskiego matematyka o nazwie Georg Cantor, który nie tylko wprowadził nieskończoność, ale także ujawnił, że było wiele nieskończoności, które istniały.
Cantor dostarczył kontrowersyjny dowód nieskończoności, który powiedział, że niektóre nieskończoności były większe niż inne. Na początku może się to wydawać niemożliwe – jak obiekt może być większy od innego obiektu, który jest nieskończony?

Kantor oparł swój dowód na gałęzi matematyki, która jest pozornie bezużyteczna: Teorii Zbiorów. Zbiór to zbiór obiektów – na przykład, możemy mieć zbiór zawierający 1, 2 i 3. Te obiekty w zbiorze nazywamy elementami.
W zapisie matematycznym wyglądałoby to następująco:
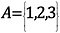
Liczba elementów w tym zbiorze, czyli kardynalność zbioru, wynosi 3.
Oznacza się to jako:
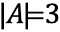
Jeśli mamy teraz inny zbiór, B, zawierający obiekty, takie, że
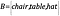
Skąd wiemy, że zbiory mają ten sam rozmiar?
Jednym ze sposobów, w jaki możemy się o tym przekonać, jest policzenie liczby elementów w drugim zbiorze. Widzimy wyraźnie, że ten zbiór również ma 3 elementy, a więc wiemy, że mają one ten sam rozmiar.
Innym sposobem, w jaki możemy to zrobić, jest porównanie naszego drugiego zbioru, B, z naszym pierwszym zbiorem, A, poprzez mapowanie.
Możemy mapować pierwszy element ze zbioru A , 1, na pierwszy element zbioru B, krzesło.
Możemy odwzorować drugi element ze zbioru A, 2, na drugi element zbioru B, stół.
Możemy odwzorować trzeci element ze zbioru A, 3, na trzeci element zbioru B, kapelusz.
Ponieważ każdy element ze zbioru A jest odwzorowywany na dokładnie 1 element ze zbioru B, zbiory te mają równą wielkość.
Przyjrzyjrzyjrzyjmy się teraz zbiorom nieskończonym. Zbiór liczb całkowitych, o którym była mowa na początku, jest zbiorem nieskończonym – istnieje nieskończenie wiele liczb całkowitych. Zbiór liczb całkowitych oznaczamy symbolem
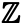
Zbiór liczb parzystych, który możemy oznaczyć jako

jest zdefiniowany jako
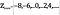
Intuicyjnie, może się wydawać
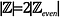
, że na każdą liczbę całkowitą parzystą przypadają 2 liczby całkowite: 1 nieparzysta liczba całkowita i 1 parzysta liczba całkowita. Sprawdźmy to.
Spróbujmy porównać zbiory przez mapowanie elementów z jednego zbioru na drugi.
Możemy mapować 1 na 2, 2 na 4, 3 na 6, itd.
Jeśli tak dalej pójdzie, zobaczymy, że każdy element ze zbioru liczb całkowitych odwzorowuje się na dokładnie 1 element ze zbioru liczb parzystych.
Tak więc, choć może się to wydawać sprzeczne z intuicją, wielkości zbiorów są równe.