Wariancja jest liczbą, która wskazuje jak bardzo zbiór liczb jest od siebie oddalony.Wariancja jest identyczna z kwadratem odchylenia standardowego i dlatego wyraża „to samo” (ale mocniej).
Wariancja – przykład
W badaniu 100 osób wykonuje proste zadanie szybkościowe w 80 próbach. Dla każdego uczestnika rejestruje się w ten sposób 80 czasów reakcji (w sekundach). Część tych danych pokazano poniżej.

W badaniach takich jak to, zwykle widzimy, że ludzie stają się szybsi, gdy częściej wykonują zadanie szybkościowe. Oznacza to, że średni czas reakcji ma tendencję do zmniejszania się na przestrzeni prób.
Również czasy reakcji będą się mniej różnić między różnymi osobami, o ile będą one częściej wykonywać zadanie. Technicznie rzecz biorąc, mówimy, że wariancja maleje na przestrzeni prób. Poniższa tabela ilustruje to dla prób 1,4,7 i 10.
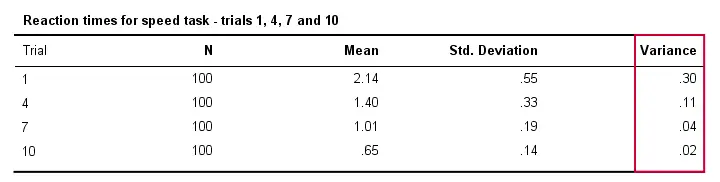
Wariancja i histogram
Doskonałym sposobem wizualizacji danych z naszej poprzedniej tabeli jest histogram dla każdej próby. W ten sposób poniższy rysunek ilustruje, że uczestnicy stawali się szybsi na przestrzeni prób; od próby 1 do próby 10 słupki histogramu przesuwają się w lewo, w kierunku 0 sekund.
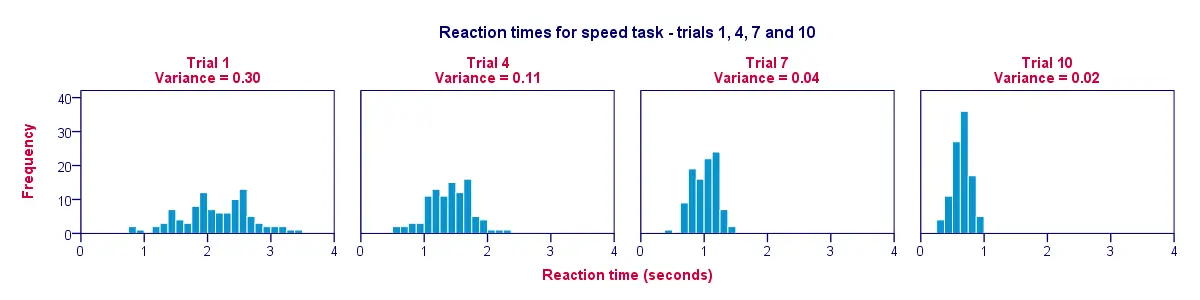
Drugim odkryciem jest to, że histogramy stają się węższe (a zatem wyższe) w miarę przechodzenia od próby 1 do próby 10; ilustruje to, że czasy reakcji różnią się coraz mniej między naszymi uczestnikami w miarę postępu eksperymentu. Wariancja maleje z upływem prób.
Wariancja – Wzór na populację
Podstawowy wzór na obliczanie wariancji to
$$S^2 = \frac{suma(X – \overline{X})^2}{n}$$
Recenzujemy, abyś spróbował zrozumieć, co ten wzór robi, ponieważ to bardzo pomaga w zrozumieniu ANOVA (= analizy wariancji). Dlatego zademonstrujemy go na zaledwie garstce danych.
Wariancja – GoogleSheets
Dla uproszczenia, ograniczymy nasze dane do pierwszej próby dla pierwszych 5 uczestników. Te 5 czasów reakcji – i ręczne obliczenie ich wariancji – znajdują się w tym arkuszu GoogleSheet.
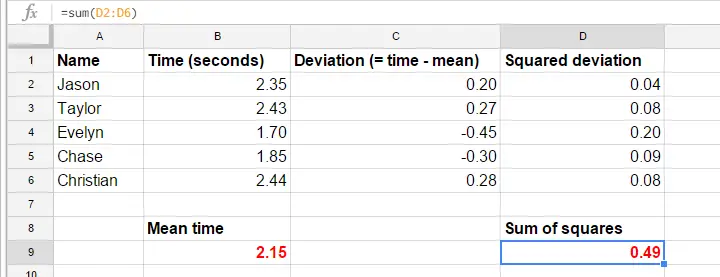
Wariancja – kroki obliczeń
Formuły w arkuszu GoogleSheet dokładnie pokazują, jak obliczyć wariancję. Podstawowe kroki to
- obliczenie średniego czasu reakcji (2,15);
- obliczenie wyników odchylenia (czas reakcji minus średni czas reakcji);
- obliczenie kwadratów wyników odchylenia;
- dodanie kwadratów wyników odchylenia. Wynik (0.49) jest sumą kwadratów, głównym elementem składowym ANOVA;
- podziel sumę kwadratów przez liczbę obserwacji (5 czasów reakcji).
Alternatywnie, oblicz wariancję wpisując =VARP(B2:B6) w jakiejś komórce (B2:B6 są komórkami, które przechowują nasze 5 czasów reakcji). VARP to skrót od „variance population” (populacja wariancji). OpenOffice i MS Excel zawierają podobne formuły.
Wariancja – przykładowa formuła
Podobnie jak w przypadku odchylenia standardowego, jeśli nasze dane są prostą próbką losową z dużo większej populacji, powyższa formuła będzie systematycznie zaniżać wariancję populacji. W tym przypadku użyjemy nieco innego wzoru:
$$S^2 = ^frac{suma(X_i – \overline{X})^2}{n – 1}$$
To, którego wzoru użyjemy, zależy więc od naszych danych: czy zawierają one całą populację, którą chcemy zbadać, czy też są zwykłą próbką z tej populacji?
Ponieważ nasze 100 uczestników jest wyraźnie próbką, użyjemy wzoru na próbkę. W GoogleSheets wpisanie =VAR(B2:B6) w jakiejś komórce zwróci wariancję z próby.
Wariancja w SPSS
O ile nam wiadomo, formuła na wariancję populacji jest całkowicie nieobecna w SPSS i uważamy to za poważną wadę. Dotyczy to zarówno wariancji międzyprzedmiotowej (omawianej w tym samouczku), jak i wariancji wewnątrzprzedmiotowej. Odpowiednie dane wyjściowe są pokazane poniżej.

W odniesieniu do tej tabeli wyjściowej, zauważ również, że wariancja jest rzeczywiście kwadratem odchylenia standardowego (poza zaokrągleniem).
W odniesieniu do wariancji, to wszystko. Mamy nadzieję, że ten poradnik okazał się pomocny w zrozumieniu czym jest wariancja.