Niepożądana konwolucja jest nieodłącznym problemem w przekazywaniu informacji analogowych. Na przykład, wszystkie z poniższych mogą być modelowane jako konwolucja: rozmycie obrazu w trzęsącej się kamerze, echo w długodystansowych rozmowach telefonicznych, nieskończona szerokość pasma analogowych czujników i elektroniki, itp. Deconvolution jestproces filtrowania sygnału w celu skompensowania niepożądanego convolution. Celem dekonwolucji jest odtworzenie sygnału w takiej postaci, w jakiej istniał on przed dokonaniem dekonwolucji. Zazwyczaj wymaga to znajomości charakterystyki konwolucji (tj. odpowiedzi impulsowej lub częstotliwościowej). Można to odróżnić od ślepej dekonwolucji, gdzie charakterystyka pasożytniczej konwolucji nie jest znana. Ślepa dekonwolucja jest znacznie trudniejszy problem, który nie ma ogólnego rozwiązania, a podejście musi być dostosowane do konkretnego application.

Deconvolution jest prawie niemożliwe do zrozumienia w dziedzinie czasu, ale quitestraightforward w dziedzinie częstotliwości. Każda sinusoida, która składa się z oryginalnego sygnału może być zmieniony w amplitudzie i / lub fazy, jak to przechodzi przez niepożądanego konwokacji. Aby wydobyć oryginalny sygnał, filtr dekonwolucji musi cofnąć te zmiany amplitudy i fazy. Dla

przykładu, jeśli konwolucja zmienia amplitudę sinusoidy o 0,5 z 30-stopniowym przesunięciem fazowym, filtr dekonwolucji musi wzmocnić sinusoidę o 2,0 z -30-stopniową zmianą fazy.

Przykład, który wykorzystamy do zilustrowania dekonwolucji to detektor promieniowania gamma. Jak pokazano na Rys. 17-3, urządzenie to składa się z dwóch części, scyntylatora i detektora światła. Scyntylator jest specjalnym rodzajem przezroczystego materiału, takiego jak jodek sodu lub germanian bizmutu. Związki te zamieniają energię każdego promienia gamma na krótki wybuch światła widzialnego. Światło to

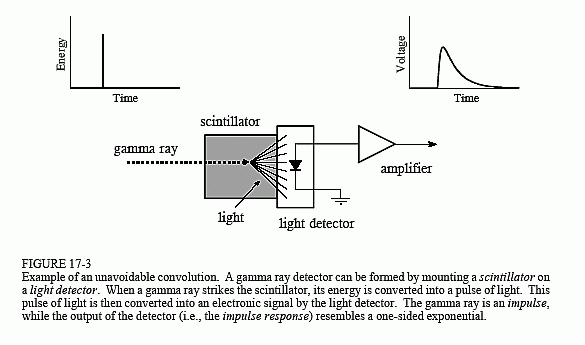
jest następnie przekształcane w sygnał elektroniczny przez detektor światła, taki jak fotodioda lub lampa fotopowielacza. Każdy impuls wytwarzany przez detektor przypomina jednostronny wykładnik, z pewnym zaokrągleniem rogów. Kształt ten jest określany przez charakterystykę użytego scyntylatora. Kiedy promień agamma umieszcza swoją energię w scyntylatorze, pobliskie atomy zostają wzbudzone do wyższego poziomu energetycznego. Atomy te ulegają losowej deekscytacji, a każdy z nich wytwarza pojedynczy foton światła widzialnego. Rezultatem netto jest impuls świetlny, którego amplituda maleje w ciągu kilkuset nanosekund (dla jodku sodu). Ponieważ pojawienie się każdego promienia gamma jest impulsem, impuls wyjściowy z detektora (tj. jednostronny wykładnik) jest odpowiedzią impulsową systemu.

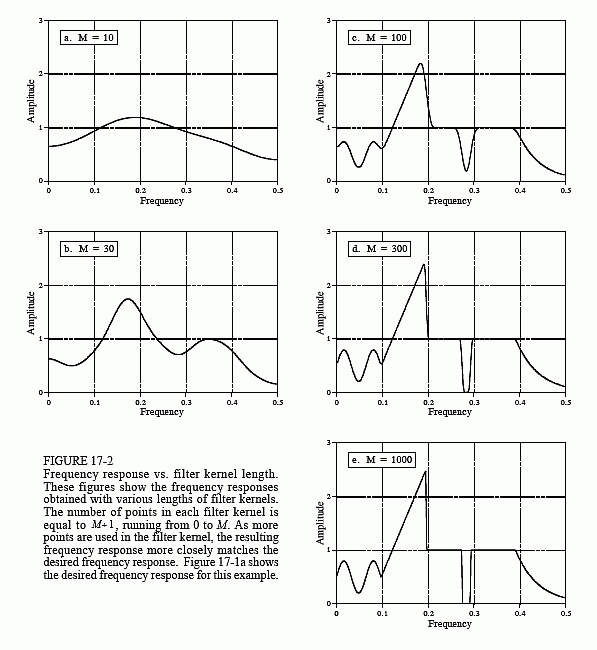
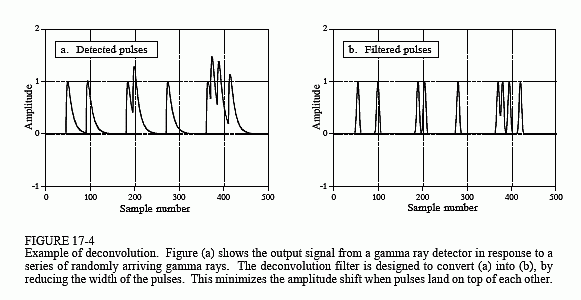
Rysunek 17-4a przedstawia impulsy generowane przez detektor w odpowiedzi na losowo przychodzące promienie gamma. Informacja, którą chcielibyśmy wydobyć z tego sygnału wyjściowego to amplituda każdego impulsu, która jest proporcjonalna do energii promienia gamma, który go wygenerował. Jest to użyteczna informacja, ponieważ energia może powiedzieć interesujące rzeczy o tym, gdzie promień gamma był. Na przykład, może to dostarczyć informacji medycznych na temat pacjenta, określić wiek odległej galaktyki, wykryć bombę w bagażu lotniczym, itp.

Wszystko byłoby w porządku, gdyby tylko sporadycznie wykrywano promienie gamma, ale zazwyczaj tak nie jest. Jak pokazano w (a), dwa lub więcej impulsów może nakładać się na siebie, przesuwając zmierzoną amplitudę. Jedną z odpowiedzi na ten problem jest dekonwolwertacja sygnału wyjściowego detektora, dzięki czemu impulsy stają się węższe, przez co występuje mniejsze spiętrzenie. Idealnie, chcielibyśmy, aby każdy impuls przypominał oryginalny impuls. Jak można przypuszczać, nie jest to możliwe i musimy zadowolić się impulsem, który ma skończoną długość, ale jest znacznie krótszy od wykrytego impulsu. Cel ten jest zilustrowany na Rys. 17-4b.

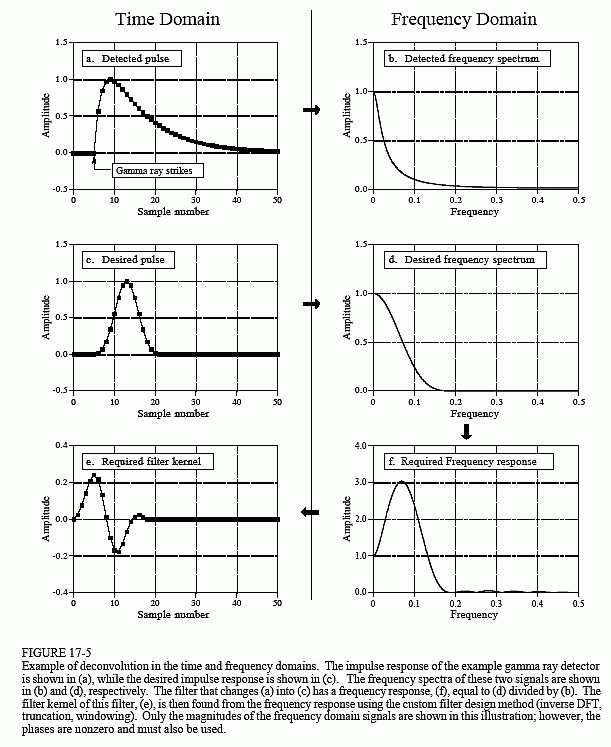
Mimo, że sygnał detektora ma zakodowaną informację w dziedzinie czasu, duża część naszej analizy musi być wykonana w dziedzinie częstotliwości, gdzie problem jest łatwiejszy do zrozumienia. Rysunek 17-5a to sygnał wytwarzany przez detektor (coś, co wiemy). Rysunek (c) jest sygnałem, który chcielibyśmy mieć (również coś, co wiemy). Ten pożądany impuls został arbitralnie wybrany tak, aby miał taki sam kształt jak okno Blackmana, o długości około jednej trzeciej długości oryginalnego impulsu. Naszym celem jest znalezienie takiego jądra filtra, (e), które po połączeniu z sygnałem z (a), daje sygnał z (c). W formie równania: jeśli a * e = c, a biorąc pod uwagę a i c, finde.

Jeśli te sygnały zostały połączone przez dodawanie lub mnożenie zamiast konwolucji, rozwiązanie byłoby proste: odejmowanie jest używane do „de-add” i dzielenie jest używane do „de-multiply”. Konwolucja jest inna; nie ma prostej operacji odwrotnej, którą można nazwać „dekonwolucją”. Konwolucja jest zbyt bałagan, aby być cofnięte przez bezpośrednie manipulowanie sygnałów w dziedzinie czasu.

Na szczęście, problem ten jest prostszy w dziedzinie częstotliwości. Pamiętaj, że konwolucja w jednej dziedzinie odpowiada mnożeniu w innej dziedzinie. Ponownie odwołując się do sygnałów z Rys. 17-5: jeśli b × f = d, a dane są b i d, znajdź f. Jest to problem łatwy do rozwiązania: odpowiedź częstotliwościowa filtra, (f), jest widmem częstotliwościowym pożądanego impulsu, (d), podzielonym przez widmo częstotliwościowe wykrytego impulsu, (b). Ponieważ wykryty impuls jest asymetryczny, będzie miał niezerową fazę. Oznacza to, że musi być użyty podział złożony (to jest, faza o wielkości & podzielona przez inną fazę o wielkości &). Na wypadek, gdybyś zapomniał, rozdział 9 definiuje jak wykonać złożony podział jednego spektrum przez drugie. Wymagane jądro filtra, (e), jest następnie znajdowane z odpowiedzi częstotliwościowej przez niestandardową metodę filtra (IDFT, przesunięcie, obcięcie, &multiplikacja przez okno).

Istnieją granice poprawy, którą może zapewnić dekonwolucja. Innymi słowy, jeśli staniesz się zachłanny, wszystko się rozpadnie. Zachłanność w tym przykładzie oznacza próbę nadmiernego zawężenia pożądanego impulsu. Przyjrzyjmy się, co się stanie. Jeśli pożądany impuls jest węższy, jego spektrum częstotliwości musi zawierać więcej składowych o wysokiej częstotliwości. Ponieważ te wysokoczęstotliwościowe składowe mają bardzo małą amplitudę w wykrytym impulsie, filtr musi mieć bardzo duże wzmocnienie przy tych częstotliwościach. Na przykład, (f) pokazuje, że niektóre częstotliwości muszą być pomnożone przez współczynnik trzy, aby osiągnąć pożądany impuls w (c). Jeżeli pożądany impuls jest węższy, wzmocnienie filtra dekonwolucyjnego będzie jeszcze większe przy wysokich częstotliwościach.

Problem polega na tym, że małe błędy są w tej sytuacji bardzo bezlitosne. Na przykład, jeśli jakaś częstotliwość jest wzmocniona przez 30, podczas gdy wymagane jest tylko 28, zdekonwertowany sygnał będzie prawdopodobnie bałagan. Kiedy dekonwolucja jest popychana do wyższych poziomów wydajności, charakterystyka niepożądanej konwolucji musi być rozumiana z większą dokładnością i precyzją. W rzeczywistych zastosowaniach zawsze istnieją niewiadome, spowodowane przez takich złoczyńców jak: szumy elektroniczne, dryf temperaturowy, różnice pomiędzy urządzeniami, itp. Te niewiadome ustawić limitonon jak dobrze deconvolution będzie work.

Nawet jeśli niechciane convolution jest doskonale zrozumiałe, nadal istnieje czynnikthat ogranicza wydajność deconvolution: szum. Na przykład, większość niechcianych konwolucji przyjmuje formę filtra dolnoprzepustowego, zmniejszając amplitudę składowych o wysokiej częstotliwości w sygnale. Dekonwolucja koryguje to poprzez wzmocnienie tych częstotliwości. Jednakże, jeśli amplituda tych składników spada poniżej nieodłącznego szumu systemu, informacja zawarta w tych częstotliwościach jest stracone. Żadna ilość przetwarzania sygnału nie jest w stanie jej odzyskać. Przepadła na zawsze. Adios! Do widzenia! Sayonara! Próba odzyskania tych danych tylko wzmocni szum. W skrajnym przypadku, amplituda niektórych częstotliwości może zostać całkowicie zredukowana do zera. To nie tylko zatrze informacje, ale będzie próbowało sprawić, że filtr dekonwolucji będzie miał nieskończone wzmocnienie na tych częstotliwościach. Rozwiązanie: zaprojektować mniej agresywny filtr dekonwolucji i / lub umieścić ograniczenia na ile wzmocnienie jest dozwolone w każdej z częstotliwości.

Jak daleko można się posunąć? Jak zachłanny jest zbyt zachłanny? To zależy całkowicie od problemu, który atakujesz. Jeśli sygnał jest dobrze zachowujący się i ma niski poziom szumu, prawdopodobnie można dokonać znaczącej poprawy (pomyśl o współczynniku 5-10). Jeśli sygnał zmienia się w czasie, nie jest szczególnie dobrze rozumiany, lub jest zaszumiony, nie osiągniesz tak dobrych wyników (myślisz o współczynniku 1-2). Udana dekonwolucja wymaga dużej ilości testów. Jeśli działa na pewnym poziomie, spróbuj pójść dalej; będziesz wiedział, kiedy się rozpadnie. Żadna ilość pracy teoretycznej nie pozwoli Ci ominąć tego mitycznego procesu.

Deconvolution może być również stosowany do sygnałów zakodowanych w dziedzinie częstotliwości. Klasycznym przykładem jest przywrócenie starych nagrań słynnego śpiewaka operowego, Enrico Caruso (1873-1921). Nagrania te zostały wykonane przy użyciu bardzo prymitywnego sprzętu jak na dzisiejsze standardy. Najistotniejszym problemem są rezonanse długiej tuby nagraniowej, służącej do zbierania dźwięku. Za każdym razem, gdy śpiewak trafia na jedną z tych częstotliwości rezonansowych, głośność nagrania gwałtownie wzrasta. Cyfrowa dekonwolucja poprawiła subiektywną jakość tych nagrań poprzez

redukcję głośnych punktów w muzyce. Opiszemy tu tylko ogólną metodę; szczegółowy opis znajduje się w oryginalnej pracy: T. Stockham, T. Cannon, andR. Ingebretsen, „Blind Deconvolution Through Digital Signal Processing”,Proc. IEEE, vol. 63, Apr. 1975, pp. 678-692.

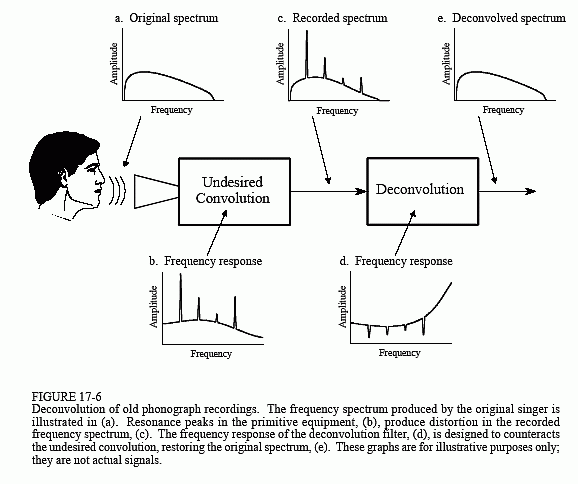
Rysunek 17-6 przedstawia ogólne podejście. Widmo częstotliwościowe oryginalnego sygnału audio jest zilustrowane na (a). Rysunek (b) pokazuje odpowiedź częstotliwościową sprzętu nagrywającego, stosunkowo gładką krzywą z wyjątkiem kilku ostrych szczytów rezonansowych. Widmo zarejestrowanego sygnału, pokazane w (c), jest równe prawdziwemu widmu, (a), pomnożonemu przez nierównomierną odpowiedź częstotliwościową, (b). Celem dekonwolucji jest przeciwdziałanie niepożądanej konwolucji. Innymi słowy, odpowiedź częstotliwościowa filtra dekonwolucji, (d), musi być odwrotnością (b). Oznacza to, że każdy szczyt w (b) jest niwelowany przez odpowiadające mu obniżenie w (d). Gdyby ten filtr był doskonale zaprojektowany, sygnał wynikowy miałby widmo, (e), identyczne z widmem oryginału.

Tutaj jest haczyk: oryginalny sprzęt nagrywający został dawno wyrzucony, a jego odpowiedź częstotliwościowa, (b), jest tajemnicą. Innymi słowy, jest to problem ślepej dekonwolucji; mając tylko (c), jak możemy określić (d)?

Problemy ślepej dekonwolucji są zwykle atakowane przez oszacowanie lub założenie dotyczące nieznanych parametrów. Aby poradzić sobie z tym przykładem, średnie widmo oryginalnej muzyki zakłada się, że odpowiada średniemu widmu tej samej muzyki wykonywanej przez dzisiejszego piosenkarza przy użyciu nowoczesnego sprzętu. Średnie widmo jest znajdowane za pomocą technik z rozdziału 9: rozbijamy sygnał na dużą liczbę segmentów, bierzemy DFT każdego segmentu, konwertujemy do postaci biegunowej, a następnie uśredniamy wielkości razem. W najprostszym przypadku, nieznana odpowiedź częstotliwościowa jest brana jako średnie widmo starego nagrania, podzielone przez średnie widmo współczesnego nagrania. (Metoda stosowana przez Stockham et al. opiera się na bardziej wyrafinowanej technice zwanej przetwarzaniem homomorficznym, zapewniając lepsze oszacowanie charakterystyki systemu nagrywania).