What is Slope Intercept Form

Slope intercept form is one of the three forms we can use to express a straight line. Pozostałe formy są nazywane formą nachylenia punktu i formą standardową, ale w tej sekcji będziemy głównie używać formy punktu przecięcia nachylenia. Używając formy przechylenia, wyrażamy równanie prostej jako:

y=mx+by = mx + by=mx+b

Możesz wiedzieć, że xxx i yyy są współrzędnymi punktu na wykresie, ale czym są mmm i bbb?

Czym jest b w y=mx+b?

Literą b jest liczba, która określa, kiedy prosta dotyka osi y. Nazywamy to również „punktem przecięcia z osią y”. Na przykład, narysujmy linię prostą na płaszczyźnie współrzędnych.

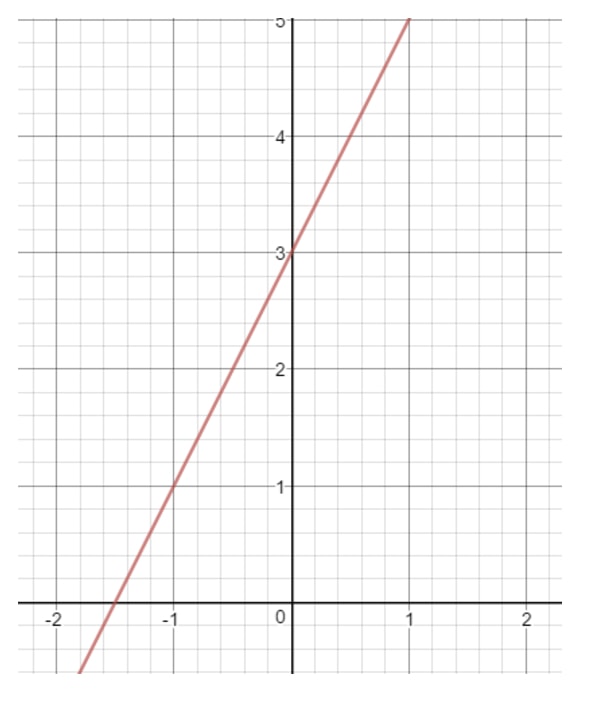
Jeśli przyjrzymy się dokładnie osi y, linia prosta dotyka osi y w określonym miejscu. Gdzie jest to miejsce? Byłaby to liczba 3, ponieważ właśnie tam oś y i prosta przecinają się. To oznacza, że możemy stwierdzić, że b = 3.

Co to jest m w postaci przechylenia linii?

Litera m jest liczbą, która reprezentuje nachylenie linii. Niektórzy ludzie nazywają nachylenie prostej wzniesieniem nad biegiem. Przypomnijmy, że jeśli mamy dwa punkty, to jesteśmy w stanie znaleźć nachylenie tych dwóch punktów, korzystając ze wzoru na nachylenie

m=riserun=y2-y1x2-x1m = \frac{wzlot}{bieg} = \frac{y_{2} – y_{1}}{x_{2} – x_{1}}m=runrise=x2-x1y2-y1

Ten sam pomysł działa tutaj. Jeśli weźmiemy dwa dowolne punkty na linii prostej, to możemy znaleźć nachylenie tej linii używając powyższego wzoru! Na przykład, użyjmy tej linii.

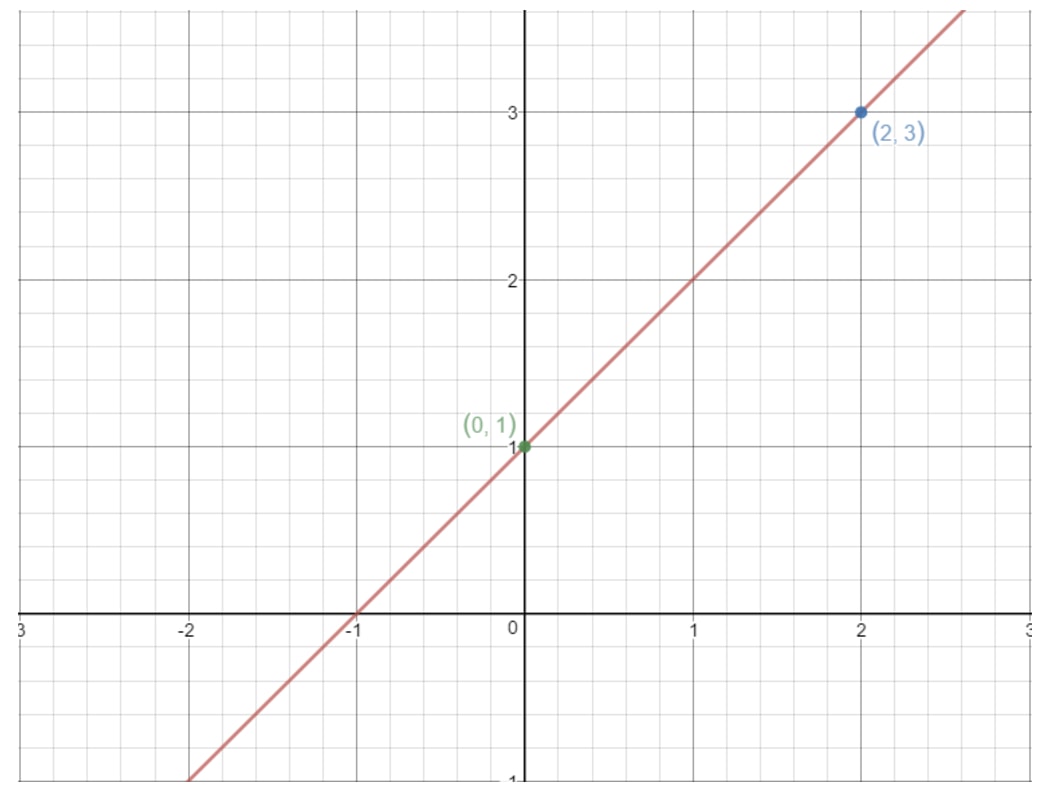
Zauważmy, że punkty (2, 3) i (0, 1) znajdują się na tym wykresie. Dlaczego więc nie użyjemy tych dwóch punktów do znalezienia nachylenia linii? Korzystając ze wzoru, otrzymalibyśmy:

m=y2-y1x2-x1=1-30-2m = \frac{y_{2} – y_{1}}{x_{2} – x_{1}} = \frac{1 – 3}{0 – 2}m=x2-x1y2-y1=0-21-3=-2-2= \frac{-2}{-2}=-2-2=1= 1=1

To oznacza, że nachylenie tej prostej wynosi 111!

Specyficzną rzeczą w przypadku nachylenia jest to, że możemy użyć dowolnych dwóch punktów na prostej, aby je znaleźć. Więc jeśli weźmiesz dwa różne punkty na tej linii, nadal otrzymasz, że nachylenie wynosi 111.

Jak napisać równanie w formie przechylenia?

Możesz wiedzieć, jak wygląda forma przechylenia, ale połowa czasu będziesz miał równania, które nie są w tej formie. Twoim zadaniem jest więc przekształcenie go w postać przechylenia. Jak to zrobić? Celem jest zawsze wyodrębnienie członu yy. Na przykład, powiedzmy, że masz równanie

6x+4+2y=06x + 4 + 2y = 06x+4+2y=0

Aby wyizolować yy, przenosimy 6x+46x + 46x+4 na prawą stronę równania

2y=-6x-42y = -6x – 42y=-6x-4

Teraz 222 przeszkadza yyy, więc pozbędziemy się go dzieląc obie strony równania przez 222.

2y2=-6x-42}{2} = \frac{-6x – 4}{2}22y=2-6x-4y=-6×2-42y = – \frac{6x}{2} – \frac{4}{2}y=-26x-24y=-3x-2y = -3x – 2y=-3x-2

Ponieważ yy jest izolowany, można zauważyć, że ma on postać pochyłą przechodnią y=mx+by = mx + by=mx+b, gdzie m=-3m = -3m=-3, a b=-2b = -2b=-2.

Teraz, gdy znamy już dobrze punkt przecięcia y i nachylenie, dlaczego nie przyjrzymy się konkretnym pytaniom dotyczącym ich znajdowania!

Jak znaleźć punkt przecięcia y?

Pytanie 1: Używając równania liniowego y=12x+5y = \frac{1}{2} x + 5y=21x+5, znajdź punkt przecięcia y.

Zauważ, że równanie ma już postać punktu przecięcia y=mx+by = mx + by=mx+b. Musimy tylko dowiedzieć się, ile wynosi bbb. Widzimy, że b=5b = 5b=5, więc punkt przecięcia y wynosi 555.

Zróbmy teraz nieco trudniejsze pytanie.

Pytanie 2: Wyznacz punkt przecięcia y równania 2x-4y=82x – 4y = 82x-4y=8

Teraz to równanie liniowe nie jest w formie punktu przecięcia zbocza, więc musimy je najpierw zmienić na tę formę. Naszym celem jest wyodrębnienie yy w tym równaniu.

Zobacz, że jeśli przeniesiemy 2x2x2x na prawą stronę równania, będziemy mieli:

-4y=8-2x-4y = 8 – 2x-4y=8-2x

Teraz dzieląc obie strony przez -4-4-4, otrzymamy:

-4y-4=8-2x-4y = \frac{8 – 2x}{-4}-4y=-48-2xy=8-4-2x-4y = \frac{8}{-4} – \frac{2x}{-4}y=-48–42xy=-2+12xy = -2 + \frac{1}{2}xy=-2+21x

Teraz zamiana miejscami dwóch członów daje nam:

y=12x-2y = \frac{1}{2}x – 2y=21x-2

Pytanie 3: Wyznacz punkt przecięcia y równania 4y-8=04y – 8 = 04y-8=0.

To może wyglądać trochę dziwnie, ponieważ nie ma tu członu xxx, ale nasz cel pozostaje ten sam. Zamierzamy wyodrębnić yyy.

Przesunięcie -8-8-8 na prawą stronę równania daje nam:

4y=84y = 84y=8

Podzielenie obu stron równania przez 444 daje nam

4y4=84 = \frac{4y}{4}44y=48y=2y = 2y=2

Teraz może to nie wyglądać, ale równanie jest w postaci nachylenia-przecinka. Chodzi o to, że m=0m = 0m=0, więc cały człon mxmxmx zniknął. Po prostu przepisz równanie jako

y=0m+2y = 0m + 2y=0m+2

Z obserwacji możesz stwierdzić, że b=2b = 2b=2, a więc punkt przecięcia y wynosi 222. Zróbmy jeszcze jedno pytanie.

Pytanie 4: Wyznacz (jeśli to możliwe) punkt przecięcia y równania 5x-15=05x – 15 = 05x-15=0.

To jest ciekawe, bo równanie nie ma wyrazu yy. Więc jak mamy je przedstawić w postaci punktu przecięcia zbocza? Cóż, jedyne co możemy teraz zrobić, to wyizolować dla xxx, więc spróbujmy tego na razie.

Przesuwając 151515 na prawą stronę równania mamy:

5x=155x = 155x=15

Podzielenie obu stron równania daje:

5×5=155=frac{5x}{5} = ^frac{15}{5}55x=515x=3x = 3x=3

Teraz narysujemy to na wykresie. Zauważmy, że w tym równaniu xxx musi być 333 i nie może być niczym innym. Jednak nie mówi ono nic o yyy, więc yyy może być czymkolwiek zechce. Gdybyśmy zapisali tablicę wartości, to otrzymamy:

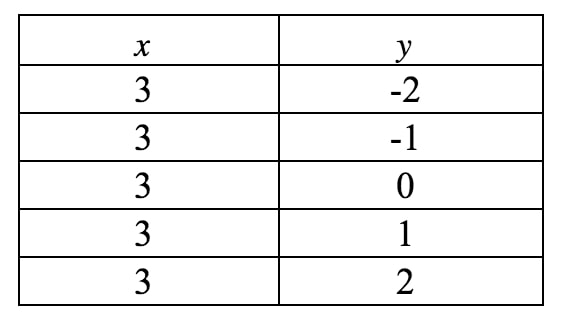
Jeśli naniesiemy te punkty na płaszczyznę współrzędnych i narysujemy prostą, to mamy:

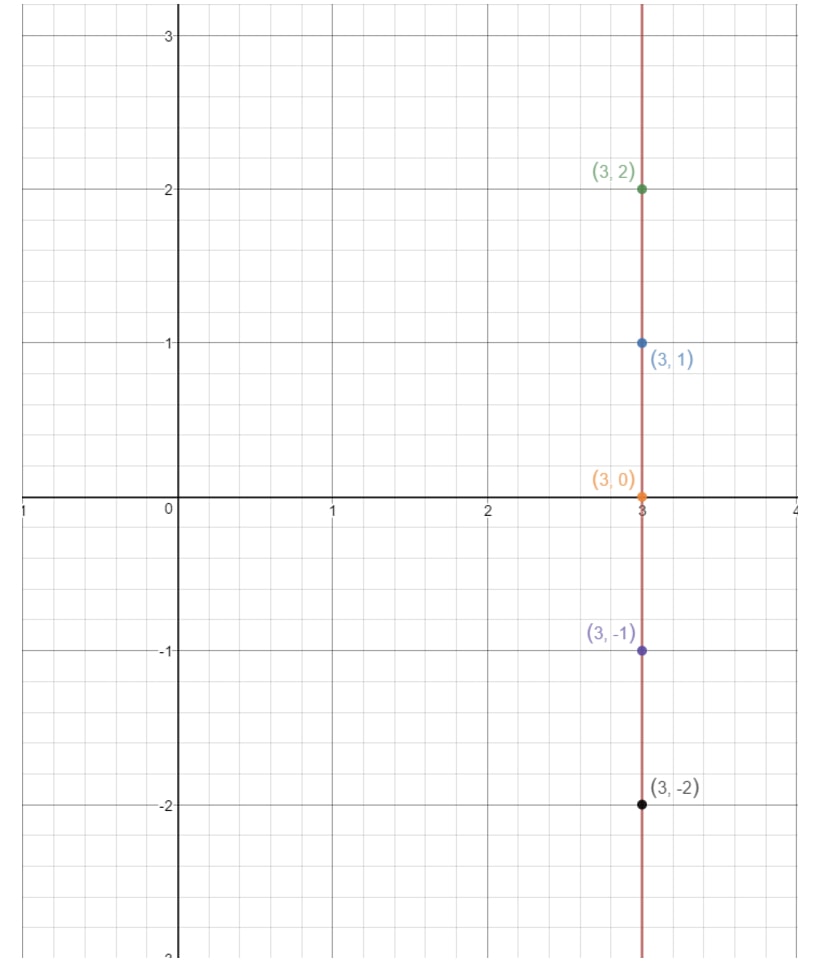
Zauważ, jak prosta nigdy nie dotyka osi y. Oznacza to, że równanie nie ma punktu przecięcia z osią y. Teraz, gdy omówiliśmy wszystkie przypadki znajdowania punktu przecięcia y, spójrzmy na pytania, które proszą nas o znalezienie nachylenia!

Jak znaleźć nachylenie równania?

Pytanie 5: Znajdź nachylenie równania y=32x+1y = \frac{3}{2}x + 1y=23x+1

Pytanie 6: Wyznacz nachylenie równania liniowego 6x-6y=06x – 6y = 06x-6y=0

Jak widzisz, równanie nie jest w postaci przechylenia y, więc musimy je najpierw przekształcić do tej postaci. Naszym celem jest wyodrębnienie yy.

Przesunięcie 6x6x6x na prawą stronę równania daje:

-6y=-6x-6y = -6x-6y=-6x

Podzielenie obu stron przez -6-6-6 daje:

-6y-6=-6x-6y = \frac{-6x}{-6}-6-6y=-6-6xy=xy = xy=x

Zauważmy, że tak naprawdę jest to w postaci przechylenia y=mx+by = mx + by=mx+b. Po prostu w tym przypadku punkt przecięcia nachylenia bbb jest równy 000, a xxx jest takie samo jak 1x1x1x. Możemy więc przepisać równanie na:

y=1x+0y = 1x + 0y=1x+0

Teraz obserwując widzimy, że m=1m = 1m=1. Skoro mmm jest nachyleniem, to nachylenie musi wynosić 111. Zróbmy teraz nieco trudniejsze

Pytanie 7: Wyznacz nachylenie odcinka 2y-4=02y – 4 = 02y-4=0

Znowu, to jest trochę dziwne, bo nie mamy żadnego członu xxx. Jednak nasz cel, aby wyodrębnić yyy, pozostaje taki sam.

Przesuwając -4-4-4 na prawą stronę równania mamy:

2y=42y = 42y=4

Podzielenie obu stron równania przez 222 daje:

2y2=42y}{2} = ^frac{4}{2}22y=24y=2y = 2y=2

Zauważ tutaj, że jest to teraz w postaci nachylenia-przechylenia, z tym, że termin mxmxmx jest ukryty, ponieważ m=0m = 0m=0. Więc możemy przepisać nasze równanie jako:

y=0x+2y = 0x + 2y=0x+2

Skoro m=0m = 0m=0, to mamy zerowe nachylenie. Jeśli zastanawiasz się, jak wygląda linia o nachyleniu 000, to tutaj jest wykres, który możesz zobaczyć.

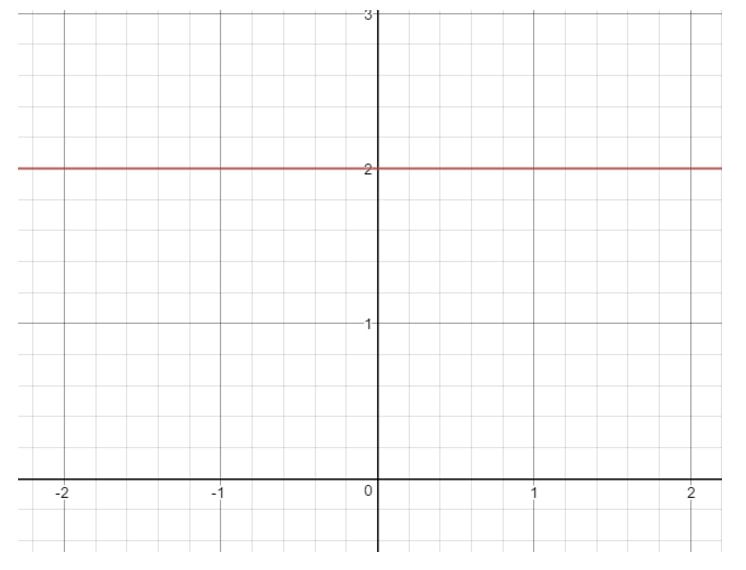
Pytanie 8: Znajdź (jeśli to możliwe) nachylenie równania liniowego 16-4x=016 – 4x = 016-4x=0

W tym przypadku nie można wyodrębnić yy, ponieważ nie ma członu yy. Więc jedyne co możemy zrobić to wyizolować xxx.

Przesunięcie 161616 na prawą stronę równania daje:

-4x=-16-4x = -16-4x=-16

Dzieląc obie strony przez -4-4-4, otrzymujemy:

-4x-4=-16-4 = -16-4x=-4-16x=4x = 4x=4

Nadal nie jest to w postaci interceptu nachylenia, więc naszą jedyną nadzieją na uzyskanie nachylenia jest narysowanie wykresu tej linii. Ponownie widzimy, że xxx jest zawsze zmuszony do 444, ale yy może być cokolwiek chce, ponieważ nie ma terminu yy. Gdybyśmy zapisali tabelę wartości, to otrzymamy:

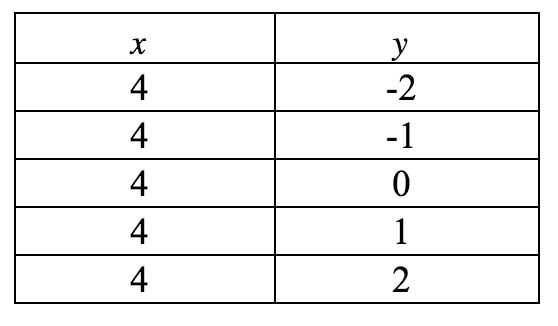
Jeśli naniesiemy te punkty na płaszczyznę współrzędnych i narysujemy prostą, to mamy:

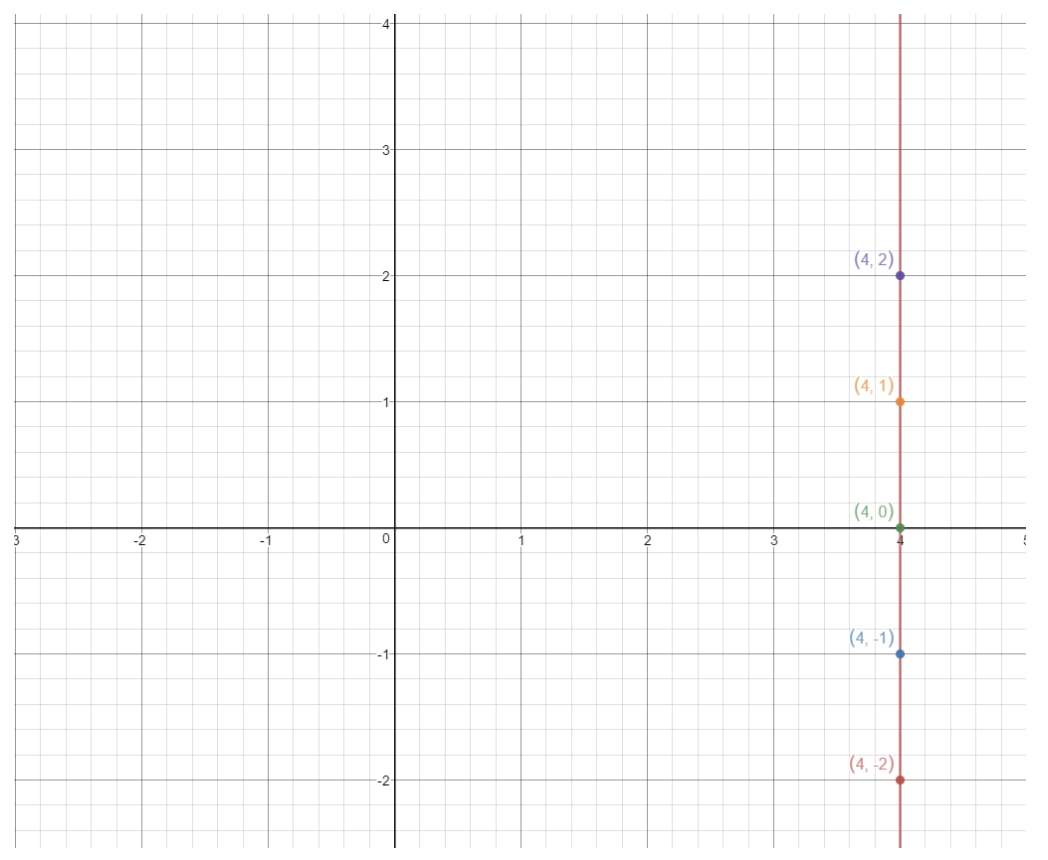
Jest to linia pionowa. Jakie jest więc nachylenie linii pionowej? Spróbujmy się tego dowiedzieć, znajdując wzniesienie i bieg. Zobacz, jak ta linia zawsze rośnie w nieskończoność, ale nie ma żadnego biegu. Więc to oznacza, że bieg wynosi 000. Jeśli więc obliczymy nachylenie, to otrzymamy:

m=riserun=rise0=undefinedm = \frac{rise}{run} = \frac{rise}{0} = undefinedm=runrise=0rise=undefined

Nie możemy podzielić przez 000, więc tak naprawdę mamy niezdefiniowane nachylenie.

Co to jest niezdefiniowane nachylenie?

Niezdefiniowane nachylenie to nachylenie, które idzie prosto w górę na wykresie. Jak widać na powyższym wykresie, nachylenie wznosi się w nieskończoność i nie ma przebiegu. W rezultacie otrzymujemy niezdefiniowane nachylenie, ponieważ nie możemy podzielić przez 000.

Ogólnie, zawsze otrzymujemy niezdefiniowane nachylenie, gdy otrzymujemy prostą pionową!

Spójrzmy na kilka innych wyjątkowych pytań!

Znajdywanie równania z jednego punktu

Pytanie 9: Punkt (2, 6) przechodzi przez równanie y=-5x+by = -5x + by=-5x+b. Znajdź „bbb”.

6=-5(2)+b6 = -5(2) + b6=-5(2)+b

Izolacja i rozwiązanie dla bbb daje:

6=-10+b6 = -10 + b6=-10+bb=16b = 16b=16

Przypomnijmy, że bbb jest również znane jako punkt przecięcia y, więc punkt przecięcia y to również 161616!

Znajdowanie nachylenia z dwóch punktów

Pytanie 10: Biorąc pod uwagę dwa punkty (6, 1) i (-10, 9), znajdź nachylenie prostej.

Przypomnij sobie, że aby znaleźć nachylenie prostej, używamy równania nachylenia

m=y2-y1x2-x1m = \frac{y_{2} – y_{1}}{x_{2} – x_{1}}m=x2-x1y2-y1

Stąd zastosowanie tego wzoru daje nam:

m=9-1-10-6=8-16m = \frac{9 – 1}{-10 – 6} = \frac{8}{-16}m=-10-69-1=-168=1-2= \frac{1}{-2}=-21

A co jeśli zamiast tego mamy znaleźć całe równanie prostej?

Równanie prostej danej w dwóch punktach

Pytanie 11: Biorąc pod uwagę dwa punkty (-6, 1) oraz (2, 6), znajdź równanie w postaci przechylenia.

Próbujemy w zasadzie znaleźć równanie w postaci y=mx+by = mx + by=mx+b. Aby to zrobić, musimy poszukać mmm i bbb.

Przypomnijmy, że aby znaleźć mmm, korzystamy z równania nachylenia

m=y2-y1x2-x1m = \frac{y_{2} – y_{1}}{x_{2} – x_{1}}m=x2-x1y2-y1

Stąd zastosowanie tego wzoru daje nam:

m=6-12-(-6)=58m = \frac{6 – 1}{2 – (-.6)} = \frac{5}{8}m=2-(-6)6-1=8558 \frac{5}{8}85

Teraz mamy więc równanie

y=58x+by = \frac{5}{8}x + by=85x+b

Teraz musimy poszukać bbb. Aby rozwiązać bbb, wybieramy któryś z podanych punktów i wstawiamy go do równania. Możemy to zrobić, ponieważ oba punkty leżą na prostej, a każdy punkt na prostej spełniałby równanie. Użyjmy punktu (2, 6). Zobaczmy, że:

6=58(2)+b6 = \frac{5}{8}(2) + b6=85(2)+b

Izolacja bb daje:

6=108+b6 = \frac{10}{8} + b6=810+bb=6-108b = 6 – \frac{10}{8}b=6-810b=488-108b = \frac{48}{8} – \frac{10}{8}b=848-810b=388b = \frac{38}{8}b=838

Przekładając to na postać dziesiętną, otrzymujemy, że b=4,75b = 4,75b=4,75. Stąd, nasze równanie postaci przechylenia wynosi:

y=58x+4.75y = \frac{5}{8}x + 4.75y=85x+4.75

Ostatnią rzeczą do omówienia w tym rozdziale jest znalezienie dziedziny i zakresu prostej.

Jak znaleźć dziedzinę i zakres?

Aby znaleźć dziedzinę prostej, zadajemy sobie pytanie: czym może być xxx? Jeśli xxx może być tymi wartościami, wtedy dodajemy je do domeny.

To samo dotyczy zakresu. Czym może być yyy? Jeśli yyy może być tymi wartościami, to dodajemy je do zakresu. Zróbmy przykład.

Pytanie 12: Znajdź dziedzinę i zakres równania y=2x+1y = 2x + 1y=2x+1.

Zauważ, że jeśli narysujemy wykres tej prostej, to otrzymamy:

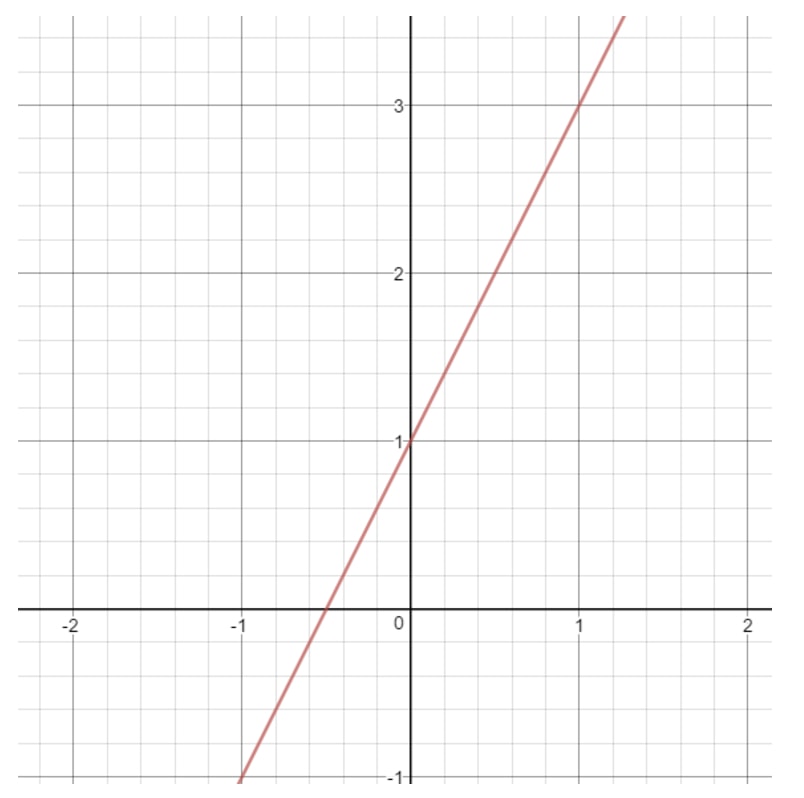
Co może być xxx w tej prostej? Zauważmy, że xxx może być czymkolwiek, ponieważ przy dowolnej wartości xxx możemy otrzymać punkt, który leży na prostej. To samo dotyczy y. Zawsze możemy wybrać wartość yy, która da nam punkt na prostej. Więc mówimy, że

Domena: {x∈∈R}Range: {y∈in∈R}

gdzie R oznacza „wszystkie liczby rzeczywiste”. Zróbmy trudniejsze zadanie.

Pytanie 13: Znajdź dziedzinę i zakres równania y=-2y = -2y=-2.

Teraz, jeśli narysujemy tę linię na wykresie, otrzymamy:

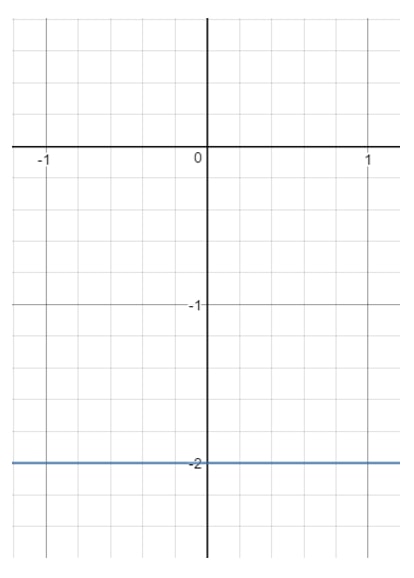
Zauważ, że xxx może być czymkolwiek, ponieważ przy dowolnej wartości xxx możemy otrzymać punkt, który leży na linii tak długo, jak długo y=-2y = -2y=-2. Spójrzmy jednak na yyy. Widzisz, że yy jest wymuszone na -2-2-2 i nie może być niczym innym. W momencie, gdy wybierzesz inną wartość yyy (jak 111), wtedy ten punkt będzie poza linią. Oznacza to więc:

Domena: {x ∈ ∈ R}Range: {y = -2}

Pytanie 14: Znajdź dziedzinę i przedział równania x=1x = 1x=1.

Teraz, jeśli narysujemy tę linię na wykresie, otrzymamy:

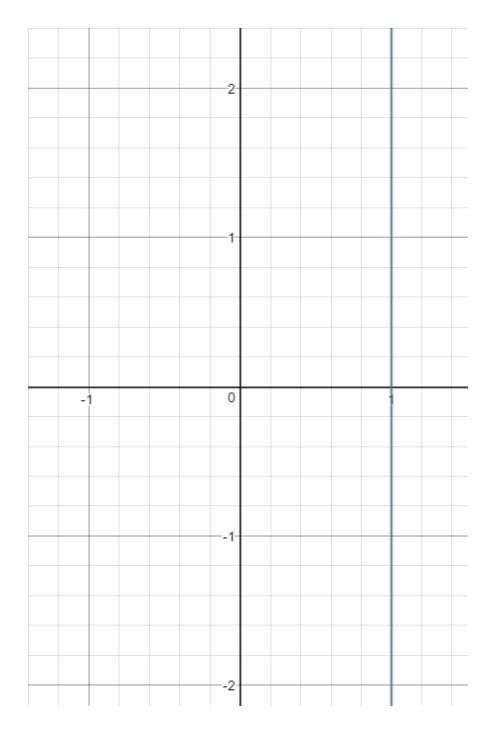
Widzisz, że xxx jest wymuszone na 111 i nie może być niczym innym. W momencie, gdy wybierzesz inną wartość xxx (np. 222), wtedy ten punkt będzie poza linią.Spójrz jednak na yyy. Zauważmy, że yyy może być czymkolwiek, ponieważ przy dowolnej wartości yyy możemy otrzymać punkt, który leży na prostej tak długo, jak x=1x = 1x=1

Więc to oznacza:

Domena: {x=1}Range: {y∈∈R}

Jeśli miałeś dużo problemów z rysowaniem wykresów, aby uzyskać dziedzinę i zakres, polecam Ci ten kalkulator.

https://www.desmos.com/calculator/2rnqgoa6a4

Uczy on, jak wykreślić równanie liniowe. Wszystko, co musisz zrobić, to wpisać wartości mmm i bbb. Następnie automatycznie narysuje linię dla Ciebie! Jest to również przydatne, gdy próbujesz znaleźć formę interceptu nachylenia.