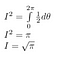Lord Kelvin napisał o tej całce: „Matematyk to ten, dla którego jest to tak oczywiste, jak to, że dwa razy dwa daje cztery jest dla ciebie.”
Zadowolenie 😉
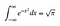
OK, więc założę, że znasz jakieś podstawowe całkowanie i różniczkowanie. Poniższy tekst doda trochę intuicji do sprytnych sztuczek, które pojawią się później. Nie przejmuj się, jeśli niektóre z nich są nieco zaskakujące, po prostu postaraj się zrozumieć, co się dzieje.
Strategią tutaj będzie dokonanie sprytnego podstawienia. Ale będziemy robić substytucję w dwóch zmiennych. Można sobie wyobrazić, że obecny problem polega na obliczaniu pola powierzchni pod krzywą
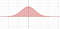
Pokażemy jednak, że problem ten można przekształcić w obliczanie objętości.
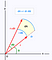
Aby obliczyć objętość, użyjemy nieco innej formuły zmiany zmiennych niż ta, której używamy w normalnych całkach. Użyjemy współrzędnych biegunowych. Wyraża to współrzędne x i y w kategoriach ich promienia i kąta. Geogebra ma ładny interaktywny sposób, aby zobaczyć to tutaj

Wtedy użyjemy magicznej formuły zmiany bazy dla współrzędnych biegunowych.
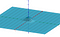
Przy obliczaniu pola powierzchni pod krzywą mieliśmy element 'dx’, który reprezentuje małą odległość wzdłuż osi x. Przy obliczaniu objętości, mamy dx dy, który jest jak mały prostokąt o długości boku dx i dy. Następnie używamy tych podstaw do tworzenia serii pudełek, które szacują objętość. Najłatwiej jest to zobaczyć na poniższej wizualizacji. Całka jest granicą tych przybliżeń.
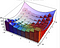
Gdy zamiast tego używamy biegunowego układu współrzędnych, mamy pod spodem nieco inny element powierzchni. Poniżej, dA jest elementem powierzchniowym. Przy niewielkich zmianach kąta i promienia, ten element powierzchni może być coraz lepiej przybliżony przez prostokąt o długościach boków odpowiednio dr i r*dtheta. Jeśli dobrze znasz się na geometrii, to dla małych wartości theta sin(theta) jest bardzo dobrze przybliżony przez theta i możesz udowodnić poniższy wynik.
Rozwiązanie całki
Najpierw nadajemy nazwę naszej całce. Nazywamy ją I.
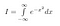
Zauważmy, że x jest tylko „zmienną dummy”. Obszar istnieje niezależnie od tego, jakiej nazwy zmiennej użyjemy. Możemy więc również napisać następujące dwa równania
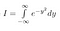
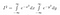
Teraz, jako że I jest tylko stałą, aczkolwiek taką, której wartości jeszcze nie znamy, możemy użyć naszych normalnych reguł sprowadzania stałej do całki
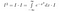
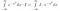
Do tej pory nie robiliśmy zbyt wiele merytorycznego. Teraz zastanowimy się mocno, co oznacza całka. Bierzemy całki z funkcji. Jeśli dwie funkcje przyjmują wszędzie tę samą wartość, to są takie same i mają tę samą dziedzinę. Mając to na uwadze, możemy wykonać następujące manipulacje, jeśli potraktujemy I*exp(-x²) jako funkcję x, czyli coś, co przyjmuje wartości x jako wejście i daje liczbę jako wyjście.
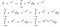
Ok, to było dużo do ogarnięcia. W pierwszej linijce po prostu przepisaliśmy I w postaci całkowej z inną nazwą zmiennej. W drugiej linii, traktując I*exp(-x²) jako funkcję, zdaliśmy sobie sprawę, że możemy sprowadzić exp(-x²) do wnętrza całki dy, a to nadal da tę samą wartość wyjściową dla dowolnej wartości wejściowej x. Wreszcie, wykorzystaliśmy reguły wykładania.
Pisząc to w całości, mamy teraz
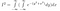
Następnie przychodzi zabójcze spostrzeżenie. Powyżej wygłupialiśmy się z nazwami zmiennych i sposobem reprezentowania funkcji. Teraz zmieniamy perspektywę: to wyrażenie reprezentuje również całkę z exp(-(y²+x²)) na całej płaszczyźnie 2D, z elementem powierzchni dA = dx dy. Tzn. dx dy jest małym prostokątem na płaszczyźnie, a exp(-(y²+x²)) jest wysokością nad tym prostokątem.
Następnie używamy spostrzeżeń o współrzędnych biegunowych z wcześniej
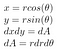
Jako sin² + cos² = 1, po podłączeniu wszystkiego, otrzymujemy
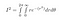
r rozciąga się od 0 do nieskończoności, a theta rozciąga się od 0 do 2*pi, ponieważ obejmuje to całą płaszczyznę 2D: każdy punkt ma promień mniejszy od nieskończoności, a kąt między 0 a 2pi radianów.
Możemy ocenić całkę wewnętrzną używając reguły łańcuchowej
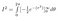
I do ziemi obiecanej teraz się znajdujemy: