Zdarzenia losowe, które mają miejsce w ciągłej przestrzeni próbek, mogą odwoływać się do wyobrażeń geometrycznych z co najmniej dwóch powodów: z powodu natury problemu lub z powodu natury rozwiązania.

Niektóre problemy, takie jak Igła Buffona, Ptaki na linie, Paradoks Bertranda, czy problem laski rozbitej na trzy kawałki, ze swej natury pojawiają się w otoczeniu geometrycznym. Ten ostatni również dopuszcza wiele przeformułowań, które wymagają porównywania pól figur geometrycznych. Ogólnie, o prawdopodobieństwach geometrycznych możemy myśleć jako o nieujemnych wielkościach (nie przekraczających 1), które są przypisane do podregionów danej dziedziny zgodnie z pewnymi regułami. Jeżeli funkcja μ jest wyrażeniem tego przyporządkowania zdefiniowanego na dziedzinie D, to na przykład wymagamy

0 ≤ μ(A) ≤ 1, A ⊂ D i
μ(D) = 1

Funkcja μ zwykle nie jest zdefiniowana dla wszystkich A ⊂ D. Te podzbiory D, dla których μ jest zdefiniowana, są zdarzeniami losowymi, które tworzą określone przestrzenie próbkowania. Bardzo często μ definiuje się za pomocą stosunku obszarów, więc jeśli σ(A) jest zdefiniowane jako „obszar” zbioru A, to można wyznaczyć μ(A) = σ(A) / σ(D).

Problem 1

Dwoje przyjaciół, którzy jeżdżą metrem do pracy z tej samej stacji, przyjeżdża na stację równomiernie losowo między 7 a 7:20 rano. Są skłonni czekać na siebie nawzajem przez 5 minut, po czym wsiadają do pociągu razem lub osobno. Jakie jest prawdopodobieństwo, że spotkają się na stacji?

W kartezjańskim układzie współrzędnych (s, t) kwadrat o boku 20 (minut) przedstawia wszystkie możliwości porannych przyjazdów dwóch przyjaciół na stację metra.

Szary obszar A jest ograniczony dwiema prostymi, t = s + 5 i t = s – 5, tak że wewnątrz A, |s – t| ≤ 5. Wynika z tego, że dwaj przyjaciele spotkają się tylko pod warunkiem, że ich przyjścia s i t wypadną w obszarze A. Prawdopodobieństwo takiego spotkania jest dane stosunkiem pola powierzchni A do pola powierzchni kwadratu:

/ 400 = 175/400 = 7/16.

Problem 2

(.)

Trzy punkty A, B, C umieszczono losowo na okręgu o promieniu 1. Jakie jest prawdopodobieństwo, że ΔABC jest ostre?.

Ustalić punkt C. Położenia punktów A i B są wtedy określone przez łuki α i β wychodzące z C w dwóch kierunkach. A priori wiemy, że 0 < α + β < 2π. Korzystne dla naszego problemu wartości α i β (jako odejmujące kąty ostre spełniają) 0 < α < π oraz 0 < β < π. Ich suma nie może być mniejsza od π, gdyż wtedy kąt C byłby rozwarty, zatem α + β > π. Sytuację tę przedstawia poniższy rysunek, na którym kwadrat ma bok 2π.

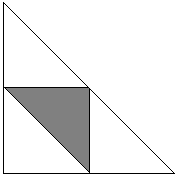
Region D jest przecięciem trzech półpłaszczyzn: 0 < α, 0 < β oraz α + β < 2π. To jest ten duży trójkąt na powyższym rysunku. Korzystne zdarzenia należą do zacieniowanego trójkąta, który jest przecięciem półpłaszczyzn α < π, β < π, oraz α + β > π. Stosunek pól tych dwóch płaszczyzn wynosi oczywiście 1/4.

Zauważmy teraz, że o ile przypadkowy trójkąt nie jest ostry, można go uważać za rozwarty, ponieważ prawdopodobieństwo, że dwa z trzech punktów A, B, C tworzą średnicę jest równe 0. (Aby BC był średnicą, powinniśmy mieć α + β = π, co jest linią prostą, z zerem jako jedynym możliwym przypisaniem powierzchni). Możemy więc powiedzieć, że prawdopodobieństwo tego, że ΔABC jest rozwartokątny wynosi 3/4. Dla trójkąta rozwartokątnego, okrąg można podzielić na dwie połowy, a trójkąt leży całkowicie w jednej z nich. Wynika stąd, że 3/4 jest odpowiedzią na następujące pytanie:

Trzy punkty A, B, C umieszczono losowo na okręgu o promieniu 1. Jakie jest prawdopodobieństwo, że wszystkie trzy leżą w półokręgu?

1. E. J. Barbeau, Murray S. Klamkin, W. O. J. Moser, Five Hundred Mathematical Challenges by (MAA, 1995, problem 244.)
2. D. A. Klain, G.-C. Rota Introduction to Geometric Probability , Cambridge University Press, 1997
3. A. A. Sveshnikov, Problems in Probability Theory, Mathematical Statistics and Theory of Random Functions, Dover, 1978
4. A. M. Yaglom, I. M. Yaglom, Challenging Mathematical Problems With Elementary Solutions, Dover, 1987

Geometric Probability

• Geometryczne prawdopodobieństwa
• Are Most Triangles Obtuse?
  • Osiem wyborów w sześciu sektorach
  • Trzy losowe punkty na okręgu
• Prawdopodobieństwo geometryczne
  • Patyk złamany na trzy kawałki (współrzędne trójliniowe)
  • Patyk złamany na trzy kawałki. Rozwiązanie we współrzędnych kartezjańskich
• Paradoks Bertranda
• Ptaki na drucie (problem i symulacja interaktywna)
  • Ptaki na drucie: Solution by Nathan Bowler
  • Birds on a Wire. Rozwiązanie Mark Huber
  • Ptaki na linie: symulacja probabilistyczna. Rozwiązanie Moshe Eliner
  • Birds on a Wire. Rozwiązanie Stuart Anderson
  • Ptaki na linie. Solution by Bogdan Lataianu
• Buffon’s Noodle Simulation
• Averaging Raindrops – an exercise in geometric probability
  • Averaging Raindrops, Part 2
• Rectangle on a Chessboard: Wprowadzenie
• Markowanie i łamanie patyków
• Losowe punkty na odcinku
• Pokrycie półkola
• Pokrycie półkuli
• Pokrycie półkuli
• Pokrywające się losowe przedziały
• Losowe przedziały with One Dominant
• Points on a Square Grid
• Flat Probabilities on a Sphere
• Probability in Triangle

|Contact||Front page|||Contents|||Up|

Copyright © 1996-…2018 Aleksander Bogomolny

.