Model Isinga jest szczególnym przykładem układu termodynamicznego, i jest to modelowy układ do zrozumienia przejść fazowych. Wiesz, że tak wielu biologów spędza tak wiele czasu z marnymi muszkami owocowymi? Cóż, fizycy spędzają mnóstwo czasu z modelem Isinga. Jak mówi nam prof. Raghu, jest to Drosophila przejść fazowych.

Personalnie, nie jestem największym fanem jego analogii, ponieważ uważam, że muszki owocowe są obrzydliwe. Mam nadzieję, że model Isinga nie będzie zbyt obrzydliwy.

Motywacja

Dlaczego powinniśmy spędzić tyle czasu rozmawiając o modelu Isinga?

• Jest on zaskakująco użyteczny, aby pomóc nam myśleć o wszelkiego rodzaju zachowaniach związanych z przejściami fazowymi. Na przykład:

  • model Isinga wykazuje łamanie symetrii w fazie niskotemperaturowej (o czym właśnie mówiliśmy)

  • posiada specjalny „punkt krytyczny” w dobrze zdefiniowanej temperaturze (do czego nawiązaliśmy w diagramie fazowym wody)

  • inne bogate właściwości.

• Jest to jeden z niewielu dokładnie rozwiązywalnych modeli, w którym możemy faktycznie obliczać wielkości termodynamiczne i interpretować je.

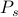  • Ogólnie, obliczanie wielkości termodynamicznych jest trudne, ponieważ musisz sumować wiele terminów. Pamiętasz z naszych pierwszych zajęć z termodynamiki, że możesz myśleć o układzie równowagi jako o zespole wielu stanów , z których każdy jest ważony własnym prawdopodobieństwem . W tych ramach, wielkości termodynamiczne, które obserwujemy odpowiadają średnim dla zespołu. W szczególności, jeśli chcesz znaleźć średnią zespołową jakiegoś obserwowalnego 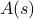, musisz znaleźć sumę 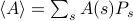, gdzie suma biegnie przez wszystkie możliwe stany. Problem z tym, jak pamiętasz, jest taki, że liczba stanów układu termodynamicznego skaluje się wykładniczo z liczbą cząstek! Nawet dla średniej wielkości układu jest po prostu zbyt wiele stanów, aby komputer mógł jednoznacznie obliczyć średnią – nie mówiąc już o układzie termodynamicznym, w którym 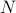jest rzędu .

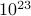  • Więc musimy ”być sprytni”, aby obliczyć funkcję podziału i powinniśmy być wdzięczni za dokładnie rozwiązywalne układy!

• Model Isinga jest prosty, ale można go zastosować do zaskakującej liczby różnych układów.

  • To nasz pierwszy przedsmak uniwersalności – cechy zjawisk krytycznych, w których ta sama teoria ma zastosowanie do wszystkich rodzajów różnych przejść fazowych, czy to w cieczach i gazach, czy w magnesach, czy w nadprzewodnikach, czy w czymkolwiek innym. Fizycy uwielbiają tego rodzaju ogólne zachowanie, ponieważ sugeruje ono pewien głębszy porządek w naszym chaotycznym świecie.

Definicja modelu Isinga

Model Isinga jest modelem matematycznym, który nie odpowiada rzeczywistemu układowi fizycznemu. Jest to ogromna (kwadratowa) siatka miejsc, gdzie każde miejsce może być w jednym z dwóch stanów. Oznaczamy każdą stronę indeksem , a dwa stany nazywamy i . Aby powiedzieć, że strona ’th jest w stanie , piszemy .

Teraz ta definicja jest żałośnie abstrakcyjna i niefizyczna, więc dla nas, fizyków, niezwykle pomocne jest posiadanie rzeczywistego systemu w umyśle, tak abyśmy mogli odnieść się do czegoś jednoznacznego i zbudować intuicję fizyczną. Oto kilka systemów fizycznych, które model Isinga może reprezentować:

• Magnes. Każda strona reprezentuje konkretny „spin” w materiale (niesparowany elektron??), i jest jeśli spin wskazuje w dół lub jeśli spin wskazuje w górę. Każdy ze spinów zachowuje się jak mini magnes z własnym mini momentem magnetycznym; jeśli wszystkie spiny są wyrównane, to cała siatka spinów zachowuje się jak duży magnes z makroskopowym momentem magnetycznym netto.

• Stop; powiedzmy, mosiądz. Każde z miejsc jest atomem w sieci; reprezentuje atom miedzi w tym miejscu; reprezentuje cynk.

• A ”gaz sieciowy”. Każde z miejsc jest możliwą lokalizacją cząstki; oznacza, że to miejsce jest puste, a oznacza, że to miejsce jest zajęte przez cząstkę.

• Bakteryjne sieci wirowe???

Na razie będziemy myśleć o modelu Isinga jako o modelu magnesu. Jest to z pewnością bardzo uproszczony i zabawkowy model magnesu, ale analogia magnesu może mimo to pomóc w kierowaniu naszą cenioną intuicją fizyczną.

Składanie Hamiltonianu

Naturalnym pytaniem, jakie można zadać o ten model magnesu jest to, jaką ma on energię. Mówiąc dokładniej, chcemy zapisać funkcję, która reprezentuje energię każdej pojedynczej możliwej konfiguracji (a.k.a. mikrostanu) spinów w magnesie. Jak wiemy, taka funkcja energii nazywana jest hamiltonianem.

W modelu Isinga hamiltonian zawiera dwa rodzaje oddziaływań:

• termin pola zewnętrznego. Jak pamiętamy z mechaniki kwantowej, zewnętrzne pole magnetyczne może rozdzielić energie stanów spin-down i spin-up, tak że jeden z nich ma wyższą energię, a drugi niższą.

  • Wielkość reprezentuje, jak silne jest pole, więc mówi nam, o ile wyższy energetycznie jest jeden spin od drugiego.

  • Znak mówi nam, czy preferowany jest spin w górę, czy w dół.

  • Ponieważ każdy pojedynczy spin odczuwa zewnętrzne pole, musimy zsumować wszystkie miejsca, aby znaleźć całkowity wkład do energii.

• termin oddziaływania pomiędzy sąsiednimi spinami – być może chcą się one ustawić w jednej linii i wskazywać w tę samą stronę, być może chcą się anty-stawić i wskazywać w różne strony. Fizycznie możemy sobie wyobrazić, że ta interakcja powstaje, ponieważ każdy spin w magnesie jest swoim własnym mini dipolem magnetycznym, który wytwarza swoje własne pole magnetyczne, a jego sąsiedzi mogą odczuwać to pole magnetyczne.

  • Rozmiar mówi jak silnie sąsiednie spiny są ze sobą sprzężone – jak bardzo chcą się (anty)wyrównać. Fizycznie, siła sprzężenia spin-spin może zależeć od odległości między nimi w siatce magetycznej, na przykład.

  • Znak mówi, czy sąsiedzi wolą się wyrównywać czy anty-równać. (Techniczny termin na to jest ferromagnetyczny lub antyferromagnetyczny, odpowiednio). Fizycznie, czy materiał jest jednym lub drugim (lub żadnym) zależy od dokładnych szczegółów mechaniki kwantowej, jak spiny oddziałują.

  • Ponieważ oddziaływanie spin-spin powstaje między dwoma spinami, musimy sumować nad parami miejsc, aby znaleźć jego całkowite oddziaływanie do energii.

Więcej o terminie interakcji

Naturalnym pytaniem dotyczącym terminu interakcji spin-spin jest to, które spiny są sprzężone z którymi spinami?

Jeżeli powrócimy do fizycznego obrazu magnesu i przybliżymy jakiś konkretny spin, będziemy oczekiwać, że siła oddziaływania spin-spin będzie silniejsza dla spinów znajdujących się w pobliżu i słabsza dla spinów oddalonych. Dokładna zależność oddziaływań spin-spin od odległości jest prawdopodobnie dość skomplikowana dla rzeczywistych magnesów.

Dla modelu Isinga przyjmujemy najprostsze możliwe założenie dotyczące natury tego oddziaływania spin-spin:

Kilka uwag:

• W kwadratowej siatce o wymiarach, każde miejsce ma 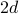najbliższych sąsiadów: w lewo i w prawo w jednym wymiarze, w górę i w dół po dodaniu drugiego wymiaru, itd…

• Zakładamy, że oddziaływanie jest izotropowe – wszyscy sąsiedzi są traktowani jednakowo niezależnie od kierunku.

• Często mówimy o oddziaływaniach w najbliższym sąsiedztwie jako o energii wiązania łączącego dwa miejsca kratowe.

• Gdy sumujemy nad sąsiednimi parami miejsc, symbolicznie piszemy małe nawiasy kątowe wokół indeksów, aby reprezentować ”najbliższego sąsiada”.

Miłą konsekwencją oddziaływań najbliższego sąsiada jest to, że gdy znajdujemy całkowitą energię jakiejś konfiguracji spinów, zamiast sumować nad wszystkimi możliwymi parami miejsc, sumujemy tylko nad parami miejsc, które sąsiadują ze sobą.

Teraz, gdy omówiliśmy wszystkie te rzeczy, jesteśmy gotowi zapisać rzeczywiste wyrażenie dla hamiltonianu. (Chciałem wyjaśnić i zinterpretować fizykę przed zapisaniem hamiltonianu, aby symbole miały jakiś sens.)

Hamiltonian modelu Isinga

Hamiltonian modelu Isinga można zapisać jako

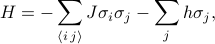
gdzie reprezentuje oddziaływanie spin-spin, reprezentuje pole zewnętrzne, a 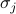są indywidualnymi spinami na każdym z miejsc kraty. Pierwsza suma jest nad wszystkimi parami sąsiednich miejsc kratowych (a.k.a. wiązania); reprezentuje oddziaływania między spinami. Druga suma jest nad wszystkimi miejscami kraty; reprezentuje zewnętrzne pole próbujące ustawić wszystkie spiny w jednym kierunku.

Dalej do termodynamiki modelu Isinga.