Jak światło odbija się lub przepuszcza od struktury materiału następuje zmiana polaryzacji. Elipsometria mierzy tę odpowiedź, która zależy od właściwości optycznych i grubości poszczególnych materiałów. Elipsometria jest używana głównie do określania stałych optycznych i grubości folii, ale także do charakteryzowania składu, krystaliczności, chropowatości, stężenia domieszek i innych właściwości materiału związanych ze zmianą odpowiedzi optycznej.
Obszary zastosowań to podstawowe badania w naukach fizycznych, półprzewodniki i rozwiązania do przechowywania danych, płaskie wyświetlacze panelowe, komunikacja, biosensory i przemysł powłok optycznych. Elipsometria posiada również elastyczność do pomiaru większości typów materiałów: dielektryków, półprzewodników, metali, nadprzewodników, organików, powłok biologicznych i kompozytów.
Definicja światła spolaryzowanego
Światło może być opisane jako fala elektromagnetyczna podróżująca przez przestrzeń. Sposób, w jaki pole fali elektromagnetycznej zachowuje się w odniesieniu do przestrzeni i czasu jest określany jako polaryzacja. Światło jest uważane za niespolaryzowane, gdy jego orientacja i faza są całkowicie dowolne. Elipsometria natomiast mierzy światło spolaryzowane – pole elektryczne, które podąża określoną ścieżką i ma wyraźny kształt w każdym punkcie. Fala elektromagnetyczna, która porusza się w kierunku z może być opisana przez jej składowe x i y, ponieważ jej pole elektryczne jest zawsze ortogonalne do kierunku propagacji. Kiedy dwie ortogonalne fale świetlne są w fazie, powstałe światło jest spolaryzowane liniowo. Jego orientacja jest określona przez względne amplitudy. Światło jest uważane za spolaryzowane kołowo, jeśli fale ortogonalne są oddalone od fazy o 90° i mają taką samą amplitudę. Najczęściej spotykana polaryzacja jest eliptyczna i łączy fale ortogonalne o dowolnych amplitudach i fazach. To właśnie stąd elipsometria bierze swoją nazwę.
Różne rodzaje polaryzacji:
Liniowa
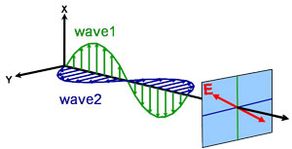
Koło
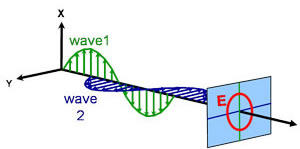
Eliptyczna
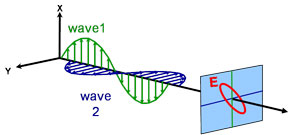
Właściwości optyczne
Właściwości optyczne, które określają sposób oddziaływania światła z materiałem, są opisywane przez dwie wartości. Zazwyczaj są one reprezentowane jako liczba zespolona. Złożony współczynnik załamania (ñ) składa się z indeksu (n) i współczynnika ekstynkcji (k):
![]()
Właściwości optyczne można również przedstawić jako złożoną funkcję dielektryczną:
![]()
z następującą zależnością między konwencjami:
![]()
Indeks przedstawia prędkość fazową światła podczas podróży w materiale w porównaniu z prędkością światła podczas podróży w próżni, c:
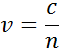
Wchodząc do materiału o wyższym indeksie światło zwalnia. Ponieważ częstotliwość fal świetlnych nie ulega zmianie, długość fali ulega skróceniu. Stratę energii fali do materiału opisuje współczynnik ekstynkcji, który jest związany ze współczynnikiem absorpcji w następujący sposób:
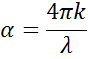
Zgodnie z prawem Beera, światło traci intensywność w materiale absorbującym. Współczynnik ekstynkcji pokazuje, jak szybko światło znika w danym materiale.
![]()
Rysunek 4 przedstawia falę świetlną przechodzącą przez dwa materiały o różnych właściwościach przed powrotem do otoczenia.
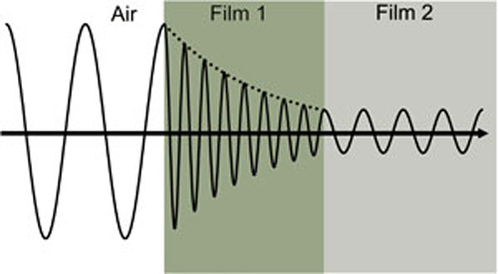
Rysunek 4: Fala świetlna przechodząca z powietrza do pochłaniającej folii 1, a następnie przezroczystej folii 2. Prędkość fazowa i długość fali zmieniają się w obu materiałach w zależności od współczynnika załamania (Folia 1: n=4, Folia 2: n=2).
Długość fali określa stałe optyczne. Rysunek 5 przedstawia stałe optyczne dla TiO2 od UV do IR. Ze względu na różne procesy, które pobierają energię z fali świetlnej, absorpcja (k>0) występuje zarówno w UV jak i IR. Absorpcja w podczerwieni jest zwykle spowodowana przez wibracje molekularne lub fononowe albo przez wolne nośniki. Absorpcja w UV zazwyczaj ma miejsce z powodu przejść elektronowych, gdzie energia światła wzbudza elektrony do podwyższonych stanów. Rysunek 5 pokazuje, że hipotetyczne lub rzeczywiste stałe optyczne nie są niezależne, ale matematycznie powiązane poprzez relacje Kramersa-Kroniga.
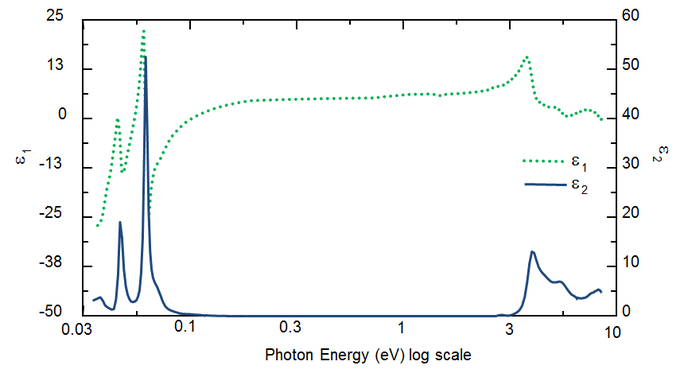
Rysunek 5: Złożona funkcja dielektryczna dla folii TiO2 o długości fali od IR (małe eV) do UV (duże eV).
Oddziaływanie światła i materiałów
Gdy światło oddziałuje z materiałem, prowadzi to do powstania warunków brzegowych na interfejsie. Podczas tego równania Maxwella muszą zawsze pozostać spełnione. Poniższy rysunek pokazuje jak padające światło odbija się i załamuje na interfejsie. Kąt pomiędzy promieniem padającym a normalną próbki (θi) będzie równy kątowi odbitemu (θr). Światło, które wnika do materiału jest załamywane pod kątem θt danym przez:
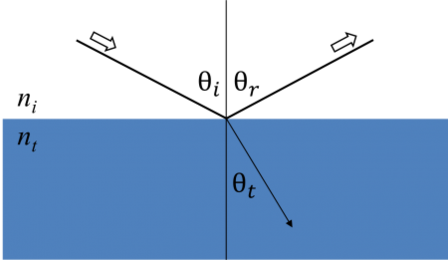
Rysunek 6: Światło odbija się i załamuje zgodnie z prawem Snella.
Na każdym interfejsie część światła jest odbijana, podczas gdy reszta przepuszcza światło pod kątem załamania. W zależności od warunków brzegowych, różne rozwiązania obowiązują dla pól elektrycznych równoległych i prostopadłych do powierzchni próbki. Światło można zatem rozdzielić na składowe ortogonalne względem płaszczyzny padania (p- i s-polaryzacja). Obie składowe mogą być obliczane oddzielnie. W ten sposób Fresnel opisał ilość światła odbitego i przepuszczonego na granicy materiałów:
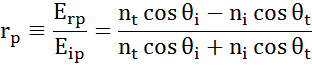
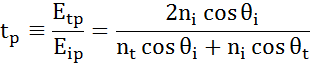
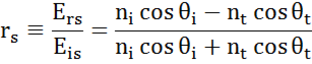
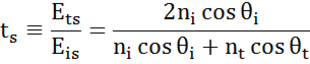
Wielokrotne interfejsy z odpowiednimi współczynnikami odbicia i transmisji Fresnela występują w przypadku cienkich folii i struktur wielowarstwowych. Aby poprawnie określić wiązkę odbitą lub transmitowaną, należy śledzić względną fazę każdej składowej światła. Grubość fazową folii wyznacza się więc w następujący sposób:
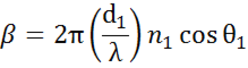
Gdy kilka fal świetlnych nakłada się na siebie, zachodzi interferencja, która zależy od fazy względnej każdej pojedynczej fali świetlnej. Poniższy rysunek przedstawia połączenie fal świetlnych w odbitej wiązce i odpowiadające im obliczenia Fresnela.
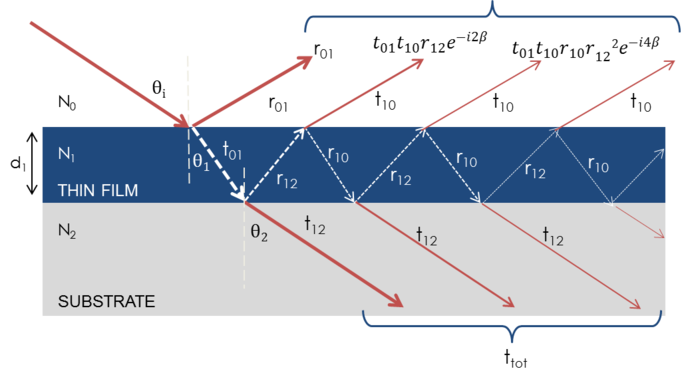
Rysunek 7: Światło odbija się i załamuje na każdym indywidualnym interfejsie, co prowadzi do powstania wielu wiązek w cienkiej folii. Interferencja wiązek zależy od względnej fazy i amplitudy pól elektrycznych. Reakcja wiązki może być obliczona przy pomocy współczynników odbicia i transmisji Fresnela.
Pomiary
Elipsometria mierzy głównie jak składowe p- i s reagują względem siebie podczas odbicia lub transmisji. Tak więc wiązka referencyjna jest zawsze częścią eksperymentu. Wiązka o znanej polaryzacji jest odbijana lub transmitowana od próbki i mierzona jest polaryzacja wyjściowa. Zmiana polaryzacji to pomiar elipsometryczny:
![]()
Rysunek 6 pokazuje typowy pomiar elipsometryczny próbki. Liniowe światło padające ma zarówno składowe p- jak i s-. Światło odbite wykazuje zmiany amplitudy i fazy zarówno dla światła spolaryzowanego p- jak i s-. Zmiany te są mierzone przez elipsometrię.

Do zbierania danych elipsometrycznych potrzebne są: źródło światła, generator polaryzacji, próbka, analizator polaryzacji i detektor. Zarówno generator polaryzacji jak i analizator zbudowane są z części optycznych, które manipulują polaryzacją: kompensatorów, polaryzatorów i modulatorów fazy. Typowe konfiguracje elipsometrów zawierają analizator rotacyjny (RAE), polaryzator rotacyjny (RPE), kompensator rotacyjny (RCE) oraz modulację fazy (PME). Na rysunku poniżej przedstawiono konfigurację RAE.
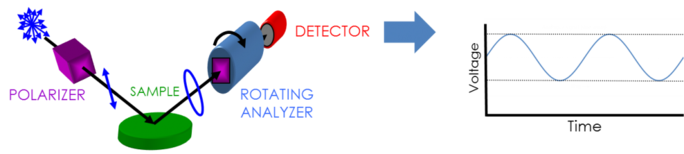
Światło niespolaryzowane jest wytwarzane przez źródło światła, a następnie przesyłane przez polaryzator. Polaryzator jest ustawiony tak, aby przepuszczał tylko światło o określonej orientacji pola elektrycznego. Ponieważ oś polaryzatora jest ustawiona pomiędzy płaszczyznami p- i s-, obydwie docierają do powierzchni próbki. Teraz liniowo spolaryzowane światło jest odbijane od powierzchni próbki, stając się eliptycznie spolaryzowane, a następnie przesyłane przez stale obracający się polaryzator („analizator”). Ilość światła, które jest przepuszczane zależy od orientacji polaryzatora w stosunku do elipsy pola elektrycznego próbki. Aby określić polaryzację odbitego światła, jest ono przekształcane na sygnał elektroniczny w detektorze. Porównanie tych danych z ustaloną polaryzacją wejściową dostarcza informacji o zmianie spowodowanej odbiciem próbki: elipsometryczny pomiar Psi i Delta.
Analiza danych
Elipsometria jest używana do określania grubości warstwy materiału lub stałych optycznych poprzez pomiar zmian w polaryzacji światła. „Pseudo” stałe optyczne z pomiaru elipsometrycznego mogą być wyprowadzone przez odwrócenie danych wyznaczonych dla pojedynczego odbicia. Jest to przydatne dla materiałów bulk.
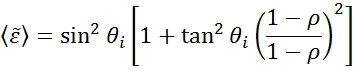
Powyższe równanie nie liczy się z żadnymi warstwami powierzchniowymi. Niemniej jednak, zwykle istnieje tlenek powierzchniowy lub chropowatość w materiałach masowych. Bezpośrednia inwersja będzie zawierała te dane jako część stałych optycznych. Na rys. 10 pokazano typowy proces analizy danych wykorzystywany w pomiarach elipsometrycznych. Ponieważ nie można napisać dokładnego równania, konieczna jest analiza regresji. Odpowiedź jest często przesadzona przy zaledwie kilku niewiadomych i setkach punktów danych eksperymentalnych. Analiza regresji pozwala na uwzględnienie wszystkich zmierzonych danych przy określaniu rozwiązania.
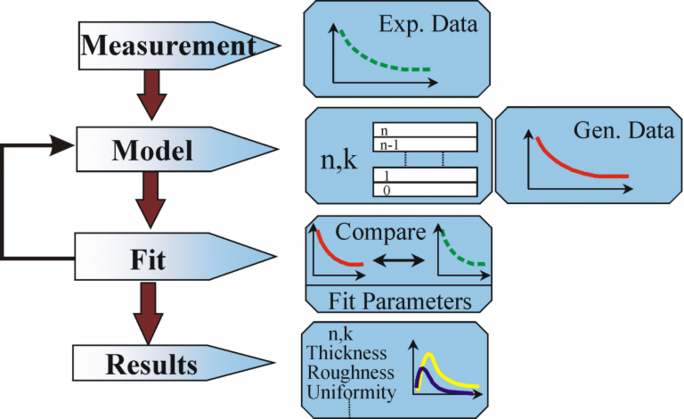
Rysunek 10: Schemat przepływu analizy danych elipsometrycznych.
W analizie danych stosowana jest następująca procedura: próbka jest mierzona i tworzony jest jej model. Za pomocą tego modelu obliczane są założone wyniki z równań Fresnela, które opisują grubość i stałe optyczne każdego materiału. Jeżeli wartości te nie są znane, dokonuje się oceny wstępnych obliczeń. Obliczone wartości są porównywane z danymi eksperymentalnymi. Aby lepiej dopasować dane doświadczalne i obliczeniowe, nieznane dane materiałowe można zmieniać. Jednakże, punktów danych doświadczalnych powinno być zawsze więcej niż nieznanych parametrów. Na przykład, maksymalnie dwie właściwości materiału mogą być określone za pomocą elipsometru o jednej długości fali, ponieważ daje on dokładnie dwa punkty danych: Ψ, Δ (Psi i Delta). Regresja jest używana do znalezienia najlepszego dopasowania pomiędzy modelem i eksperymentem. Różnica pomiędzy krzywymi danych jest określana ilościowo za pomocą estymatora, takiego jak średni błąd kwadratowy (MSE). Nieznane właściwości są zmieniane aż do osiągnięcia minimalnej wartości MSE. Oznacza to, że najniższy MSE jest równoznaczny z najlepszą odpowiedzią.
Zobacz na poniższym rysunku krzywą MSE w zależności od grubości folii dla przezroczystej folii na krzemie. Najniższa wartość MSE występuje przy grubości 749 nm, pomimo wielu minimów lokalnych. Zatem prawidłowa grubość folii to również 749 nm. Algorytm regresji może uznać lokalne minimum za prawidłowe. Zatem, aby określić prawidłowe minimum globalne, mądrze jest porównać wyniki na oko pod kątem najniższego MSE.
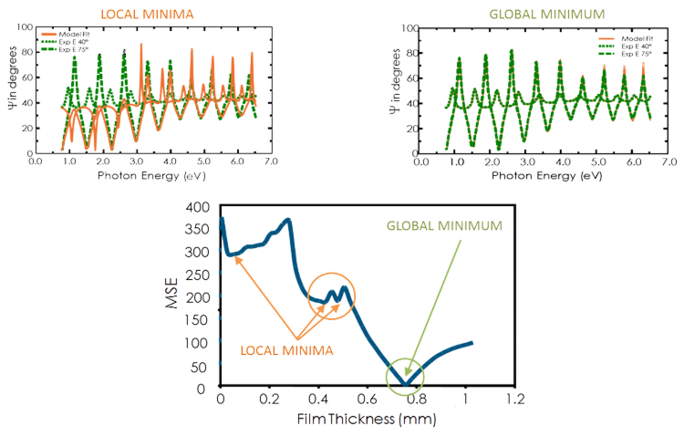
Rysunek 11, góra-prawa: Dane eksperymentalne i odpowiadające im krzywe wygenerowane dla modelu przy minimum globalnym. Rysunek 11, góra-lewa: Podobna krzywa na lokalnym minimum w pobliżu grubości 0,45 µm może być łatwo zidentyfikowana jako wynik nieprawidłowy. Rysunek 11, dół: Krzywa MSE w zależności od grubości pokazuje globalne minimum. Algorytm regresji może dać lokalne minima, ale nie wynik końcowy.
Określanie grubości folii
Grubość folii jest zwykle określana przez interferencję pomiędzy światłem, które odbija się od powierzchni i światłem, które przechodzi przez folię. Czy ta interferencja jest uważana za konstruktywną czy destruktywną zależy od względnej fazy światła, które łączy się z odbiciem od powierzchni. Interferencja zawiera zarówno informację amplitudową jak i fazową. Informacja fazowa z Δ jest bardzo czuła dla warstw o grubości poniżej monowarstwy. Zobacz poniższy rysunek dla porównania intensywności odbicia i elipsometrii dla tej samej serii cienkich warstw SiO2 na Si. Reflektancja dla każdej warstwy jest prawie taka sama, podczas gdy występują duże różnice w Δ.
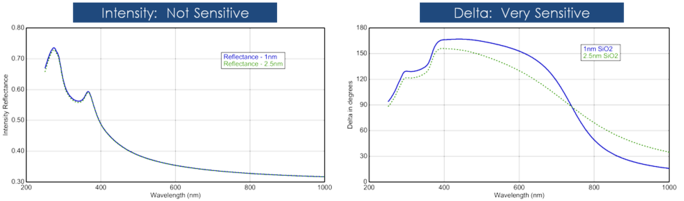
Rysunek 12, po lewej: Odbita intensywność i elipsometryczna delta (po prawej) dla dwóch cienkich tlenków na krzemie. Pomiar intensywności nie pokazuje, że Delta jest bardzo czuła dla filmów o skali nanometrowej.
Ellipsometria jest powszechnie stosowana dla filmów o grubości od sub-nanometrów do kilku mikronów. W przypadku filmów grubszych niż kilkadziesiąt mikronów, oscylacje interferencyjne mogą być rozwiązane z coraz większym trudem, z wyjątkiem sytuacji, gdy używane są dłuższe fale podczerwone. Dlatego dla grubszych folii stosuje się zwykle inne techniki pomiarowe.
Aby zmierzyć grubość, część światła musi przejść przez całą folię, a następnie powrócić na powierzchnię. W przypadku materiałów pochłaniających światło, optyczne pomiary grubości mogą być wykonywane tylko na cienkich i półprzezroczystych warstwach, chyba że są one wykonywane w regionach spektralnych o mniejszej absorpcji. Na przykład, folia organiczna, która absorbuje światło UV i IR może być przezroczysta przy średnich długościach fal widzialnych. Metale silnie absorbują na wszystkich długościach fal, więc maksymalna grubość warstwy, która może być określona wynosi około 100 nm.
Stałe optyczne
Stałe optyczne odgrywają ważną rolę w pomiarach grubości. Grubość folii wpływa na długość drogi światła, które przez nią przechodzi, indeks określa prędkość fali świetlnej i kąt załamania. Oba te czynniki wpływają na opóźnienie pomiędzy światłem przechodzącym przez folię a odbiciem od powierzchni. Konieczne jest ustalenie n i k, jak również grubości, aby uzyskać prawidłowe wyniki pomiaru optycznego.
Ponieważ stałe optyczne materiału różnią się dla różnych długości fal, wszystkie długości fal, które są analizowane za pomocą elipsometru, muszą być indywidualnie określone. Reakcja materiału przy każdej długości fali może być przewidziana przy użyciu tabeli stałych optycznych. Aby uniknąć żmudnego dopasowywania nieznanych stałych optycznych długość fali do długości fali, korzystne jest jednoczesne wykorzystanie wszystkich długości fal. Regulowane parametry relacji dyspersji pozwalają na przykład na dopasowanie ogólnego kształtu stałej optycznej do wyników eksperymentalnych. W porównaniu z ustawianiem indywidualnych wartości n i k dla każdej długości fali, liczba nieznanych wolnych parametrów jest znacznie zredukowana.
Zależności Cauchy’ego lub Sellmeiera są często używane do opisu indeksu dla materiałów przezroczystych, gdzie zależność Cauchy’ego jest zwykle podawana jako:
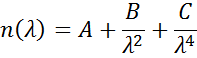
z trzema warunkami dopasowanymi tak, aby odpowiadały współczynnikowi załamania dla danego materiału. Zależność Cauchy’ego nie jest ograniczona spójnością Kramersa-Kroniga (KK) i może prowadzić do niefizycznego rozproszenia. Z drugiej strony, relacja Sellmeiera narzuca spójność Kramersa-Kroniga (KK), która zapewnia, że dyspersja optyczna zachowuje realistyczny kształt. Relacja Sellmeiera jest zwykle zapisywana jako:
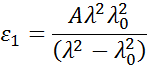
Materiały absorbujące często mają przezroczysty obszar długości fali, który może być modelowany za pomocą relacji Cauchy’ego lub Sellmeiera. Jednakże, region absorpcji musi uwzględniać zarówno rzeczywiste, jak i urojone stałe optyczne. Aby opisać absorpcję dla różnych materiałów, wiele relacji dyspersji wykorzystuje teorię oscylatorów, w tym Lorentza, Harmonic i Gaussa. Wszystkie one mają podobne atrybuty, przy czym cechy absorpcji są opisywane za pomocą amplitudy, poszerzenia i energii ośrodka (związanej z częstotliwością światła). Kształt składowej rzeczywistej jest obliczany przy użyciu konsystencji Kramersa-Kroniga, po tym jak zachowanie urojone jest opisane przez oscylator. Aby uwzględnić ewentualną dodatkową absorpcję poza mierzonym obszarem spektralnym, do składnika rzeczywistego dodawane jest przesunięcie. Oscylator Lorentza może być zapisany jako:
![]()
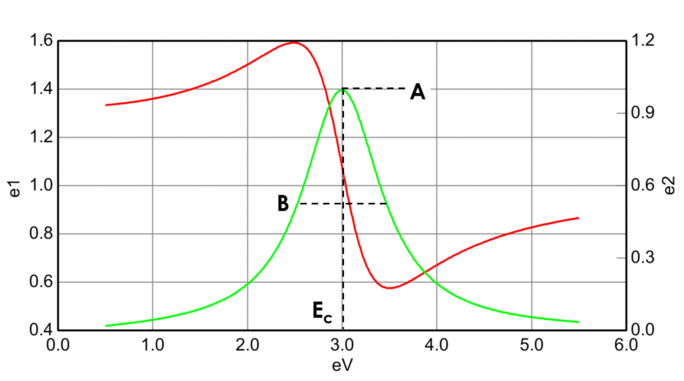
Rysunek 13 pokazuje również amplitudę (A), poszerzenie (B), energię centralną (Ec) i przesunięcie (e1, off set) dla typowego oscylatora Lorentza. Energia E jest związana z częstotliwością fali, n:
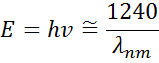
Stała Plancka h i długość fali λ są podane w nanometrach. Inne modele dyspersji, takie jak Tauc-Lorentz i Cody-Lorentz, zawierają terminy opisujące energię przerwy pasmowej.
Dalsza lektura
Ellipsometria jest uznaną techniką optyczną służącą do pomiaru cienkich warstw i materiałów sypkich. Wykorzystuje zmiany polaryzacji spowodowane odbiciem/przesłanianiem od struktury materiału do określenia jego właściwości, takich jak grubość i stała optyczna.
Aspnes D.E. (1985). The Accurate Determination of Optical Properties by Ellipsometry. In: Palik E.D. (ed.) Handbook of Optical Constants of Solids, pp. 89-112. Academic Press, Orlando.
Azzam R.M.A. and Bashara N.M. (1987). Ellipsometry and Polarized Light, Elsevier Science B.V., Amsterdam, The Netherlands.
Boccara A.C., Pickering C., and Rivory J. (eds.), (1993). Spectroscopic Ellipsometry, Elsevier Publishing, Amsterdam.
Collins R.W., Aspnes D.E., and Irene E.A. (eds.), (1998). „Proceedings from the Second International Conference on Spectroscopic ellipsometry”. In: Thin Solid Films, vols. 313-314.
Fujiwara H., Spectroscopic Ellipsometry, Principles and Applications, John Wiley & Sons, Ltd. 2007
Gottesfeld S., Kim Y.T., and Redondo A. (1995). „Recent applications of ellipsometry and spectroellipsometry in electrochemical systems”, In: I. Rubinstein (ed.), Physical Electrochemistry: Principles, Methods, and Applications, Marcel Dekker, New York.
Herman, I.P. (1996). Optical Diagnostics for Thin Film Processing, pp 425-479. Academic Press, San Diego, California.
Johs B. et al (1999). „Przegląd spektroskopowej elipsometrii o zmiennym kącie (VASE), część II: Zaawansowane zastosowania”. Optical Metrology, vol. CR72, pp 29-58. SPIE, Bellingham, Washington.
Johs B. et al (2001). „Recent Developments in Spectroscopic Ellipsometry for in situ Applications”. In: Duparré A, Singh B (ed.) Optical Metrology Roadmap for the Semiconductor, Optical, and Data Storage Industries II, vol. 4449, pp 41-57. SPIE, Bellingham, Washington.
Roseler A. (1990). Infrared Spectroscopic Ellipsometry, Akademie-Verlag, Berlin.
Rossow U. i Richter W. (1996). „Elipsometria spektroskopowa” w: Bauer G i Richter W (eds.) Optical Characterization of Epitaxial Semiconductor Layers, pp. 68-128, Springer-Verlag, Berlin.
Tompkins H.G. (1993). A User’s Guide to Ellipsometry, Academic Press, San Diego, California.
Tompkins H.G. and McGahan W.A. (1999). Spectroscopic Ellipsometry and Reflectometry, John Wiley & Sons, Inc, USA.
Tompkins, H.G. and Irene E.A. (eds.), 2005, Handbook of Ellipsometry, William Andrew Publishing, New York.
Tompkins, H. G. and Hilfiker, J. H., Spectroscopic Ellipsometry, Practical Application to Thin Film Characterization, 2016, Momentum Press Engineering
Woollam J.A. and Snyder P.G. (1992). „Variable Angle Spectroscopic Ellipsometry” w: Brundle CR, Evans CA, and Wilson S (eds) Encyclopedia of Materials Characterization: Surfaces, Interfaces, Thin Films, pp. 401-411, Butterworth-Heinemann, Boston.
Woollam J.A. et al (1999). „Overview of Variable Angle Spectroscopic Ellipsometry (VASE), Part I: Basic Theory and Typical Applications”. Optical Metrology, vol. CR72, pp 3-28. SPIE, Bellingham, Washington.
Woollam J.A. (2000). „Ellipsometry, Variable Angle Spectroscopic” w: Webster J.G. (ed.) Wiley Encyclopedia of Electrical and Electronics Engineering, pp. 109-116. John Wiley & Sons, New York.
.