Jak obliczyć napięcie w linach zawieszających obiekt

Możemy zobaczyć na poniższej ilustracji, że siła, F, potrzebna do podniesienia obiektu jest równa ciężarowi, W, obiektu. Ta idea jest podstawowym pojęciem, na którym opiera się nasz wzór na siłę naciągu. Poniżej znajduje się również diagram ciała swobodnego obiektu, który pokazuje siły rozciągające, T, działające na strunę. Jak widać, siły napięcia występują parami i w przeciwnych kierunkach:

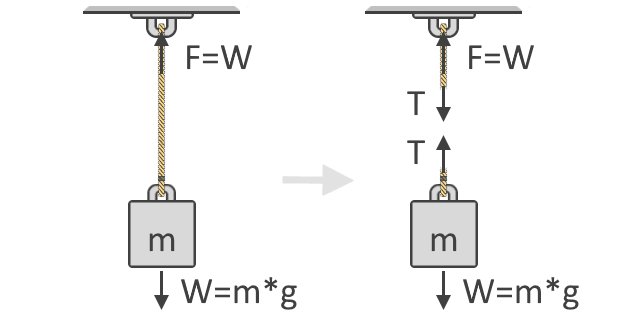
Podążając za Drugim Prawem Ruchu Newtona, możemy następnie wyrazić sumę sił za pomocą diagramu swobodnego ciała obiektu, jak pokazano po prawej stronie powyższej ilustracji. Używamy diagramów swobodnego ciała, aby pokazać różne kierunki i wielkości sił działających na ciało. W równowadze wszystkie te siły powinny być równe zeru. Uznając wszystkie siły działające w górę za dodatnie, a w dół za ujemne, nasze równanie ma postać:

ΣF = 0 = T + (-W)
T = W
gdzie masa, W, staje się ujemna, ponieważ jest skierowana w dół. Przenosząc W na drugą stronę równania, możemy teraz zobaczyć, że siła napięcia w linie jest równa ciężarowi przedmiotu, który ona przenosi, jak również pokazano powyżej.

Jeśli użyjemy więcej lin do podniesienia przedmiotu, całkowita siła napięcia zostanie podzielona na liny. Siła napięcia w każdej z lin zależy od ich kąta w stosunku do kierunku siły, której się przeciwstawiają. Aby lepiej to zrozumieć, rozważmy inny diagram swobodnego ciała obiektu zawieszonego na dwóch linach, jak pokazano poniżej:

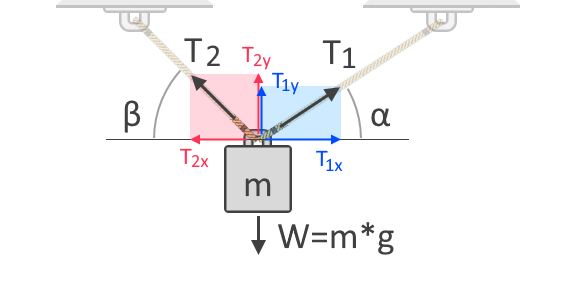
Na diagramie swobodnego ciała pokazanym powyżej widzimy składowe poziome i pionowe sił rozciągających, T₁ i T₂. Siły są wektorami, co oznacza, że zawsze mają zarówno wielkość, jak i kierunek. Jak wszystkie wektory, siły można wyrazić za pomocą tych składowych, co daje wpływ siły wzdłuż osi poziomej i pionowej. T₁ₓ i T₂ₓ to składowe pionowe odpowiednio T₁ i T₂. Z drugiej strony, T₁ᵧ i T₂ᵧ są pionowymi składowymi tych samych sił, odpowiednio. Ponieważ grawitacja działa na obiekt w osi pionowej, musimy uwzględnić pionowe składowe sił rozciągających w naszym sumowaniu sił w następujący sposób:

ΣF = 0 = T₁ᵧ + T₂ᵧ + (-W)
W = T₁ᵧ + T₂ᵧ

Ponieważ znamy również kąty sił rozciągających, możemy wyrazić T₁ᵧ i T₂ᵧ w terminach T₁ i T₂, odpowiednio, za pomocą funkcji trygonometrycznych:

T₁ᵧ = T₁ * sin(α)
T₂ᵧ = T₂ * sin(β)
W = T₁ * sin(α) + T₂ * sin(β)

Możemy również powiedzieć, że aby układ był w równowadze, obiekt nie powinien poruszać się poziomo ani wzdłuż osi x. Zatem składowe poziome T₁ i T₂ muszą być równe zeru. Ponadto, z pomocą trygonometrii, możemy wyrazić T₁ₓ i T₂ₓ odpowiednio w kategoriach T₁ i T₂:

T₁ₓ = T₂ₓ
T₁ * cos(α) = T₂ * cos(β)

Jeśli podzielimy obie strony przez cos(α), to otrzymamy równanie, w którym T₁ wyraża się w terminach T₂ i kątów:

T₁ = T₂ * cos(β) / cos(α)

Możemy następnie użyć tego równania do rozwiązania dla T₂ poprzez podstawienie T₂ * cos(β) / cos(α) jako T₁ w naszym równaniu sumowania sił, jak pokazano poniżej:

W = T₁ * sin(α) + T₂ * sin(β)
W = T₂ * * sin(α) + T₂ * sin(β)
W = T₂ *
T₂ = W /

Ostatecznie, jeśli pomnożymy całe to równanie przez cos(β) / cos(α), tak jak wyprowadziliśmy wartość T₁ w postaci T₂, a następnie upraszczając wszystko, otrzymamy to równanie:

T₁ = W / *
T₁ = W / *
T₁ = W /

Teraz wystarczy znać kąty lin napinających względem poziomu. Jeśli podany jest kąt od pionu, wystarczy odjąć ten kąt od 90°. W ten sposób otrzymamy kąt od poziomu. Jeśli jednak podano inne wartości kątów, które mogą być większe niż 90° lub nawet 180°, warto sprawdzić nasz kalkulator kątów odniesienia, aby pomóc w określeniu potrzebnego kąta. Po określeniu wartości zmiennych w naszych wzorach na siłę naciągu, możemy teraz rozwiązać siły naciągu.