by Marco Taboga, PhD
Funkcja wskaźnikowa zdarzenia jest zmienną losową, która przyjmuje wartość 1, gdy zdarzenie ma miejsce i wartość 0, gdy zdarzenie nie ma miejsca. Funkcje wskaźnikowe są często używane w teorii prawdopodobieństwa w celu uproszczenia notacji i udowodnienia twierdzeń.

Definicja
Poniżej znajduje się formalna definicja.
Definicja Niech  będzie przestrzenią próbkową, a
będzie przestrzenią próbkową, a  będzie zdarzeniem. Funkcja wskaźnika (lub wskaźnikowa zmienna losowa) zdarzenia
będzie zdarzeniem. Funkcja wskaźnika (lub wskaźnikowa zmienna losowa) zdarzenia  , oznaczana przez
, oznaczana przez  , jest zmienną losową zdefiniowaną w następujący sposób:
, jest zmienną losową zdefiniowaną w następujący sposób: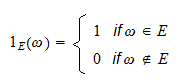
Podczas gdy wskaźnik zdarzenia  jest zwykle oznaczany przez
jest zwykle oznaczany przez  , czasami jest on również oznaczany przez
, czasami jest on również oznaczany przez , gdzie
, gdzie  jest grecką literą Chi.
jest grecką literą Chi.
Przykład Rzucamy kością i jedna z sześciu liczb od 1 do 6 może pojawić się twarzą do góry. Przykładowa przestrzeń to Zdefiniuj zdarzenie
Zdefiniuj zdarzenie  opisane zdaniem „Parzysta liczba pojawia się twarzą do góry”. Zmienna losowa, która przyjmuje wartość 1, gdy parzysta liczba pojawia się twarzą do góry i wartość 0 w przeciwnym przypadku jest wskaźnikiem zdarzenia
opisane zdaniem „Parzysta liczba pojawia się twarzą do góry”. Zmienna losowa, która przyjmuje wartość 1, gdy parzysta liczba pojawia się twarzą do góry i wartość 0 w przeciwnym przypadku jest wskaźnikiem zdarzenia  . Przypadkowa definicja tego wskaźnika to
. Przypadkowa definicja tego wskaźnika to
Z powyższej definicji łatwo można zauważyć, że  jest dyskretną zmienną losową o wsparciu
jest dyskretną zmienną losową o wsparciu  i funkcji masy prawdopodobieństwa
i funkcji masy prawdopodobieństwa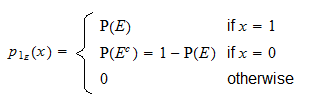
Właściwości
Funkcje wskaźnikowe korzystają z następujących własności.
Potęgi
 -trzecia potęga
-trzecia potęga  jest równa
jest równa  :
: ponieważ
ponieważ  może być albo
może być albo  albo
albo  i
i
Wartość oczekiwana
Wartość oczekiwana  jest równa
jest równa  :
: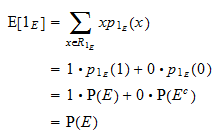
Wariancja
Wariancja  jest równa
jest równa  . Dzięki zwykłemu wzorowi na wariancję i powyższej własności potęg otrzymujemy
. Dzięki zwykłemu wzorowi na wariancję i powyższej własności potęg otrzymujemy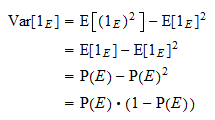
Intersekcje
Jeśli  i
i  są dwoma zdarzeniami, to
są dwoma zdarzeniami, to przyp:
przyp:
-
if
 , then
, then  and
and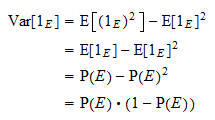
-
if
 , then
, then and
and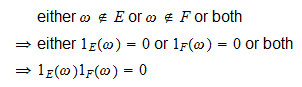
Wskaźniki zdarzeń o prawdopodobieństwie zerowym
Niech  będzie zdarzeniem o prawdopodobieństwie zerowym, a
będzie zdarzeniem o prawdopodobieństwie zerowym, a  zmienną losową całkowitą. Wówczas,
zmienną losową całkowitą. Wówczas, Pomimo, że rygorystyczny dowód tego faktu wykracza poza zakres tego wprowadzenia, własność ta powinna być intuicyjna. Zmienna losowa
Pomimo, że rygorystyczny dowód tego faktu wykracza poza zakres tego wprowadzenia, własność ta powinna być intuicyjna. Zmienna losowa  jest równa zero dla wszystkich punktów próby
jest równa zero dla wszystkich punktów próby  z wyjątkiem ewentualnie punktów
z wyjątkiem ewentualnie punktów  . Wartość oczekiwana jest średnią ważoną wartości, jakie może przyjąć
. Wartość oczekiwana jest średnią ważoną wartości, jakie może przyjąć  , gdzie każda wartość jest ważona przez odpowiednie prawdopodobieństwo. Niezerowe wartości, jakie może przyjąć
, gdzie każda wartość jest ważona przez odpowiednie prawdopodobieństwo. Niezerowe wartości, jakie może przyjąć  są ważone zerowymi prawdopodobieństwami, więc
są ważone zerowymi prawdopodobieństwami, więc  musi wynosić zero.
musi wynosić zero.
Rozwiązane ćwiczenia
Poniżej znajdziesz kilka ćwiczeń z objaśnionymi rozwiązaniami.
Ćwiczenie 1
Rozważmy zmienną losową  oraz inną zmienną losową
oraz inną zmienną losową  zdefiniowaną jako funkcja
zdefiniowaną jako funkcja  .
.
Wyrazić  za pomocą funkcji wskaźnikowych zdarzeń
za pomocą funkcji wskaźnikowych zdarzeń  i
i  .
.
Zaznaczamy przez  wskaźnik zdarzenia
wskaźnik zdarzenia  i oznaczamy przez
i oznaczamy przez  wskaźnik zdarzenia
wskaźnik zdarzenia  . Możemy zapisać
. Możemy zapisać  jako
jako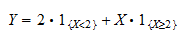
Ćwiczenie 2
Niech  będzie zmienną losową dodatnią, to znaczy taką, która może przyjmować tylko wartości dodatnie. Niech
będzie zmienną losową dodatnią, to znaczy taką, która może przyjmować tylko wartości dodatnie. Niech  będzie stałą. Udowodnij, że
będzie stałą. Udowodnij, że  gdzie
gdzie  jest wskaźnikiem zdarzenia
jest wskaźnikiem zdarzenia  .
.
Pierw zauważ, że suma wskaźników  i
i  jest zawsze równa
jest zawsze równa  :
: W konsekwencji możemy napisać
W konsekwencji możemy napisać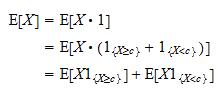 Teraz zauważ, że
Teraz zauważ, że  jest zmienną losową dodatnią, a wartość oczekiwana zmiennej losowej dodatniej jest dodatnia:
jest zmienną losową dodatnią, a wartość oczekiwana zmiennej losowej dodatniej jest dodatnia: Tym samym,
Tym samym,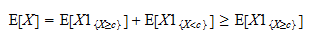
Ćwiczenie 3
Niech  będzie zdarzeniem i oznaczmy jego funkcję wskaźnikową przez
będzie zdarzeniem i oznaczmy jego funkcję wskaźnikową przez  . Niech
. Niech  będzie dopełnieniem
będzie dopełnieniem  i oznaczmy jego funkcję wskaźnikową przez
i oznaczmy jego funkcję wskaźnikową przez  . Czy można wyrazić
. Czy można wyrazić  jako funkcję
jako funkcję  ?
?
Suma dwóch wskaźników jest zawsze równa  :
: Therefore,
Therefore,
How to cite
Please cite as:
Taboga, Marco (2017). „Funkcje wskaźnikowe”, Wykłady z teorii prawdopodobieństwa i statystyki matematycznej, Wydanie trzecie. Kindle Direct Publishing. Dodatek online. https://www.statlect.com/fundamentals-of-probability/indicator-functions.