Zero jest liczbą, która mieści się dokładnie pomiędzy liczbami dodatnimi i ujemnymi na linii liczbowej. Zero jest uważane za liczbę całkowitą, wraz z dodatnimi liczbami naturalnymi (1, 2, 3, 4…) i liczbami ujemnymi, (…-4,-3,-2,-1).

Zero jest szczególną liczbą w liczbach całkowitych, ponieważ jest jedyną liczbą całkowitą, która nie jest ani dodatnia, ani ujemna. Jest to również jedyna liczba całkowita, która nie jest ani liczbą pierwszą, ani złożoną. Jest uważana za liczbę parzystą, ponieważ jest podzielna przez 2 bez reszty. Zero jest elementem tożsamości addytywnej w różnych systemach algebry, a cyfra „0” jest używana jako wartość zastępcza w systemach notacji pozycyjnej do reprezentowania liczb.

Zero ma wiele interesujących właściwości, które czynią je przedmiotem zainteresowania matematyków. Jeśli dodamy lub odejmiemy zero od dowolnej liczby, to liczba pozostaje taka sama Jeśli pomnożymy 0 przez dowolną liczbę, to wynikiem będzie 0. Każda liczba podniesiona do potęgi zerowej ma wartość 1, a więc 20=1 i 560=1. W tradycyjnej algebrze dzielenie przez 0 jest niezdefiniowane, więc żadna liczba nie może być podzielna przez 0. Liczba 0 jest również elementem liczb rzeczywistych i zespolonych.

Historia liczby 0

Skąd wzięła się idea zera? Dziś wydaje nam się to intuicyjne; zero to liczba, która oznacza ilość zerową – nic. Widzimy zera wszędzie w społeczeństwie i naturalnie rozumiemy, co one oznaczają i jak można nimi matematycznie manipulować. Historycznie jednak, koncepcja 0 zajęło dość dużo czasu, aby być powszechnie uznane za obiekt matematyki, a wielu w historii argumentował, że liczba zero nie istnieje, lub że pomysł zero jest niespójne pojęcie.

Wiele starożytnych społeczeństw nie miał wyraźną koncepcję ilości zero lub konkretnej cyfry do wykorzystania do jego reprezentacji. Starożytni Egipcjanie i Babilończycy mieli jakąś ideę zerowej ilości i potrzebę wartości zastępczych w reprezentacji liczb, ale nigdy nie rozwinęli odrębnej cyfry lub koncepcji do reprezentowania tej ilości lub wartości zastępczej. Starożytne egipskie systemy numeracji były całkowicie obrazkowe i nie miały wartości pozycyjnych, a starożytni Babilończycy używali spacji między liczbami do reprezentowania wartości pozycyjnych.

Majowie mieli wyraźną koncepcję 0 i mieli odrębną cyfrę do reprezentowania koncepcji i używania jako wartości zastępczej w ich systemie kalendarza vigesimal (base-20). Podczas gdy Majowie, Olmekowie i inne prekolumbijskie społeczeństwa były jednymi z pierwszych w historii, które miały wyraźne i wyrafinowane zrozumienie liczby 0, systemy te nie miały wpływu na społeczeństwa Starego Świata w Europie.

Starożytni Grecy, z drugiej strony, mieli skomplikowany związek z zerem. Nie mieli symbolu dla jego koncepcji lub dla niego jako wartości zastępczej, ponieważ nie byli pewni, czy liczba 0 może być uważana za rzeczywiście istniejącą rzecz. Jak, pytali, coś (liczba) może być niczym (zerem)? Dla Greków liczby naturalne (1, 2, 3, 4,…) wywodziły się z naszego rozumienia dyskretnych pojedynczych obiektów w świecie. Arystoteles sam słynny argumentował, że 0 nie istnieje, na tej podstawie, że 0 reprezentuje pustkę lub nicość, a prawdziwa pustka lub nicość nie może istnieć.

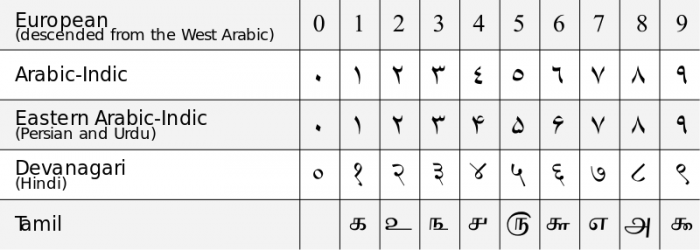
Chińczycy rozumieli „0” jako cyfrę zastępczą dla ich systemów liczenia, ale nie uważali, że cyfra „0” reprezentuje jakąkolwiek odrębną liczbę, tylko użyteczny symbol. Powszechne rozumienie 0 jako odrębnej liczby i jako cyfry dla systemów notacji pozycyjnej przyszło z Indii w 6 wieku naszej ery. Ówcześni matematycy indyjscy opracowali pierwsze rodzaje systemów notacji dziesiętnej (podstawa 10), które uwzględniały 0 jako odrębną cyfrę i rozumieli wyjątkowe właściwości matematyczne zera. Do XI w. n.e. idea zera rozprzestrzeniła się w Europie Zachodniej pod wpływem matematyków islamskich żyjących w Hiszpanii pod kalifatem Umajjadów, a współczesny arabski system notacji dziesiętnej został stworzony. Pierwsze użycie angielskiego słowa „zero” datuje się na rok 1589.

Matematyczne właściwości zera

Liczba zero odgrywa integralną rolę w niemal każdej dziedzinie matematyki. Zero jest najmniejszą nieujemną liczbą całkowitą i nie ma żadnej liczby naturalnej, która by ją poprzedzała. Ponieważ 0 jest liczbą całkowitą, jest również liczbą racjonalną, liczbą rzeczywistą i liczbą złożoną. W matematyce, 0 jest uważane za wielkość, która odpowiada zeru. Można powiedzieć, że zero jest „ilość” posiadanych przez zestaw, który nie ma członków.

W algebrze

W algebrze elementarnej, zero jest często wyrażane jako leżące w środku linii liczbowej. Liczba 0 jest uważana za liczbę parzystą, ponieważ jest całkowitą wielokrotnością liczby 2 (2×0=0). 0 nie jest liczbą pierwszą, ponieważ ma nieskończoną liczbę czynników, i nie jest liczbą złożoną, ponieważ żaden iloczyn dwóch liczb pierwszych nie jest równy liczbie 0.

W odniesieniu do 4 głównych operatorów arytmetycznych (+, -, ×, ÷) oraz operacji wykładnika, liczba 0 zachowuje się zgodnie z następującymi regułami:

• Dodawanie: x+0=0+x=x. Zero jest uważane za element tożsamości addytywnej, ponieważ każda liczba plus lub minus zero jest równa tej liczbie
• Odejmowanie: x-0=x i 0-x=-x
• Mnożenie: x⋅0=0⋅x=0. Każda liczba razy 0 jest również równa 0.
• Dzielenie: 0/x=0, z wyjątkiem sytuacji, gdy x=0. x/0 jest matematycznie niezdefiniowana wielkość, jak 0 nie ma multiplikatywny odwrotność (żadna liczba razy 0 daje 1).
• Exponents: x0=1, z wyjątkiem, gdy x=0. Od dawna debata na temat tego, czy 00 jest niezdefiniowany lub dobrze sformułowane wyrażenie. For all positive x, 0x=0.

W wyrażeniach dotyczących granic, ilość 0/0 może pojawić się w kontekście demonstrowania granic funkcji racjonalnych takich jak f(x)/g(x). W tych przypadkach, 0/0 nie jest niezdefiniowany, ale reprezentuje nieokreśloną formę. Nie oznacza to, że granica jest nieokreślona, ale że musi być obliczona za pomocą innej metody, takiej jak znajdowanie pochodnych. Istnieją pewne modele algebraiczne, w których dzielenie przez zero daje określoną wielkość, takie jak rzutowo rozszerzona linia rzeczywista lub sfera Riemanna.

W teorii zbiorów

W teorii zbiorów, liczba 0 odpowiada kardynalności „pustego zbioru” lub „zbioru zerowego” (powszechnie reprezentowanego jako {} lub {∅}. Kardynalność zbioru to ilość elementów w tym zbiorze, jeśli ktoś nie ma żadnych pomarańczy, to ma zbiór 0 pomarańczy (pusty zbiór pomarańczy).

Zero jest często używane jako punkt wyjścia w teorii zbiorów do konstruowania reszty liczb naturalnych. Te konstrukcje von Neummana, nazwane tak na cześć znanego polimaty Johna von Neumanna, konstruują liczby naturalne przez zdefiniowanie 0={} i definiują funkcję następnika S(a) = a ∪ {a}. Całą liczbę naturalną można skonstruować z rekurencyjnych zastosowań funkcji następnika, zaczynając od zbioru pustego:

0 = {}

1 = 0 ∪ {0} = {{}

2 = 1 ∪ {1} = {0,1} = {{}, {{}}

3 = 2 ∪ {2} = {0, 1, 2} = {{}, {{}}, {{}, {{}}}}

i tak dalej. Idąc tym tropem, można skonstruować cały nieskończony zbiór liczb naturalnych. W ten sposób możemy powiedzieć, że każdej liczbie naturalnej odpowiada zbiór zawierający wszystkie liczby naturalne przed nią.

W fizyce

W kontekście dokonywania pomiarów ilościowych w fizyce, 0 jest uważane za linię bazową, od której dokonywane są wszystkie inne pomiary jednostek. Bardzo często linia bazowa 0 odpowiada jakiejś fizycznie istotnej zmiennej, która jest naturalnie odróżnialna od wszystkich innych wielkości pomiarowych.

Na przykład, w skali Kelvina, temperatura 0 K odpowiada absolutnemu 0 – najzimniejszej temperaturze, która jest fizycznie możliwa. W skali Celsjusza temperatura 0 °C jest zdefiniowana jako punkt zamarzania wody przy ciśnieniu atmosferycznym. W kontekście dynamiki i elektromagnetyzmu, wartość 0 jest nadawana pozycji, w której układ ma minimalną możliwą ilość energii potencjalnej. Na przykład, stan podstawowy atomu, najniższy możliwy poziom energii dla elektronów w atomie, jest często przypisywany wartości 0.

Podobnie, w kontekście kinematyki, ramka odniesienia, z której dokonuje się obserwacji ruchu, jest zdefiniowana jako posiadająca punkt środkowy leżący na początku osi współrzędnych w punkcie (0, 0). W przypadku zachowanych wielkości, takich jak masa-energia, pęd i moment pędu, całkowita ilość zmian zachowanych wielkości w izolowanym systemie jest zawsze równa 0.

W Informatyce

Komputery przechowują informacje w postaci bitów-długich sekwencji 1s i 0s. W tej binarnej reprezentacji, 0 odpowiada pozycji „off” i jest skontrastowane z pozycją „on” oznaczoną przez 1. Wartość 0 na obwodzie elektrycznym oznacza, że obwód jest wyłączony i nie ma żadnego przepływu elektrycznego. Podobnie wiele logik obliczeniowych definiuje „0” jako znak, który reprezentuje fałszywą wartość prawdy.

W komputerowych bazach danych elementy tablicy są liczone przy użyciu systemu liczenia opartego na zerze. Oznacza to, że dla zestawu z n elementami, elementy mają indeksy zaczynające się od 0. Tak więc, element o numerze indeksu 0 jest w rzeczywistości pierwszym elementem w serii, a numer indeksu 1 odpowiada drugiemu elementowi, i tak dalej. Ogólnie rzecz biorąc, n-ty termin zestawu ma numer indeksu odpowiadający n-1. Ten system liczenia może być mylący dla nowych programistów, którzy są przyzwyczajeni do intuicyjnego przypisywania wartości indeksów zaczynających się od 1.