Nul is een getal dat vierkant tussen de positieve en negatieve getallen op de getallenlijn valt. Nul wordt beschouwd als een geheel getal, samen met de positieve natuurlijke getallen (1, 2, 3, 4…) en de negatieve getallen, (…-4,-3,-2,-1).
Nul is een speciaal getal in de gehele getallen, omdat het het enige gehele getal is dat noch positief noch negatief is. Het is ook het enige gehele getal dat noch een priemgetal noch een samengesteld getal is. Het wordt beschouwd als een even getal omdat het deelbaar is door 2 zonder rest. Nul is het additieve identiteitselement in verschillende algebrastelsels, en het cijfer “0” wordt gebruikt als plaatsvervangende waarde in positionele notatiesystemen om getallen weer te geven.
Zero heeft vele interessante eigenschappen die het interessant maken voor wiskundigen. Als je van een willekeurig getal nul aftrekt of optelt, blijft het getal gelijk. Als je 0 met een willekeurig getal vermenigvuldigt, is het resultaat 0. Elk getal tot de macht nul is 1, dus 20=1 en 560=1. In de traditionele algebra is deling door 0 niet gedefinieerd, dus geen enkel getal kan worden gedeeld door 0. Het getal 0 is ook een element van de reële getallen en de complexe getallen.
Geschiedenis van het getal 0
Waar komt het idee van nul vandaan? Tegenwoordig lijkt het voor ons intuïtief; nul is een getal dat staat voor een nietige grootheid – een niets. We zien overal nullen in de maatschappij, en we begrijpen natuurlijk wat ze betekenen en hoe ze wiskundig gemanipuleerd kunnen worden. Historisch gezien heeft het echter lang geduurd voordat het begrip 0 universeel werd erkend als een voorwerp van de wiskunde, en velen in de geschiedenis hebben betoogd dat het getal nul niet bestaat, of dat het idee nul een onsamenhangend concept is.
Vele oude samenlevingen hadden geen expliciet concept van de hoeveelheid nul of een specifiek cijfer om het voor te stellen. De oude Egyptenaren en de Babyloniërs hadden beide wel enig idee van een nulgrootheid en een behoefte aan plaatshouders in de voorstelling van getallen, maar zij ontwikkelden nooit een apart cijfer of concept om die grootheid of plaatshouderwaarde voor te stellen. De oude Egyptische getallenstelsels waren volledig picturaal en kenden geen positiewaarden, terwijl de oude Babyloniërs spaties tussen de getallen gebruikten om positiewaarden weer te geven.
De Maya’s hadden wel een expliciet concept van 0 en hadden een apart cijfer om het concept weer te geven en te gebruiken als plaatshouderwaarde in hun vigesimale (basis-20) kalendersysteem. Hoewel de Maya’s, de Olmeken en andere pre-Colombiaanse samenlevingen tot de eersten in de geschiedenis behoorden met een expliciet en verfijnd begrip van het getal 0, hebben deze systemen de samenlevingen in de Oude Wereld in Europa niet beïnvloed.
De Oude Grieken daarentegen hadden een gecompliceerde relatie met nul. Zij hadden geen symbool voor het concept ervan of voor het als een plaatsvervangende waarde, omdat zij niet zeker wisten of het getal 0 als een werkelijk bestaand ding kon worden beschouwd. Hoe, vroegen zij zich af, kon iets (een getal) niets (nul) zijn? Voor de Grieken waren de natuurlijke getallen (1, 2, 3, 4,…) afgeleid van ons begrip van discrete individuele objecten in de wereld. Aristoteles zelf beweerde dat 0 niet bestaat, omdat 0 een leegte of niets voorstelt, en een echte leegte of niets kan niet bestaan.
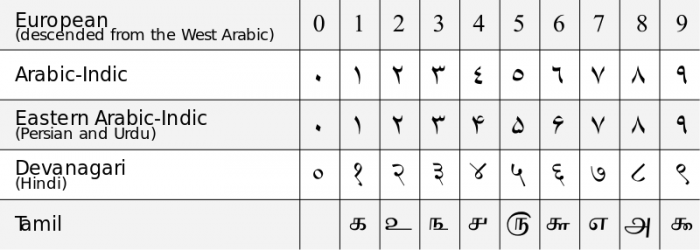
De Chinezen hadden een begrip van “0” als een plaatsvervangend cijfer voor hun telsystemen, maar zij beschouwden het cijfer “0” niet als een afzonderlijk getal, alleen als een nuttig symbool. Het algemene begrip van 0 als een afzonderlijk getal en als een cijfer voor positionele notatiesystemen kwam uit India in de 6e eeuw na Christus. Indiase wiskundigen ontwikkelden in die tijd de eerste decimale (basis-10) notatiesystemen waarin 0 als afzonderlijk cijfer werd opgenomen en zij hadden een goed begrip van de unieke wiskundige eigenschappen van nul. Tegen de 11e eeuw na Christus had het idee van de nul zich verspreid naar West-Europa via de invloed van islamitische wiskundigen die in Spanje leefden onder het Umayyad kalifaat, en werd het hedendaagse Arabische cijferstelsel van de decimale notatie gecreëerd. Het eerste gebruik van het Engelse woord “zero” dateert van 1589.
Mathematische eigenschappen van nul
Het getal nul speelt een integrale rol in bijna elk gebied van de wiskunde. Nul is het kleinste niet-negatieve gehele getal en heeft geen natuurlijk getal dat erboven staat. Omdat 0 een geheel getal is, is het ook een rationaal getal, een reëel getal en een complex getal. In de wiskunde wordt 0 beschouwd als een grootheid die overeenkomt met een nulhoeveelheid. Men zou kunnen zeggen dat nul de “hoeveelheid” is die een verzameling bezit die geen leden heeft.
In de algebra
In de elementaire algebra wordt nul vaak uitgedrukt als liggend in het midden van de getallenlijn. Het getal 0 wordt beschouwd als een even getal omdat het een geheel veelvoud is van het getal 2 (2×0=0). 0 is geen priemgetal omdat het een oneindig aantal factoren heeft, en het is geen samengesteld getal omdat geen enkel product van twee priemgetallen gelijk is aan het getal 0.
Met betrekking tot de 4 hoofdrekenkundige operatoren (+, -, ×, ÷) en de exponentoperatie gedraagt het getal 0 zich volgens de volgende regels:
- Toevoeging: x+0=0+x=x. Nul wordt beschouwd als het additieve identiteits-element, want elk getal plus of min nul is gelijk aan dat getal
- Aftrekking: x-0=x en 0-x=-x
- Vermenigvuldiging: x⋅0=0⋅x=0. Elk getal maal 0 is ook gelijk aan 0.
- Deling: 0/x=0, behalve wanneer x=0. x/0 is een wiskundig ongedefinieerde grootheid, want 0 heeft geen multiplicatieve inverse (geen enkel getal maal 0 geeft je 1).
- Exponenten: x0=1, behalve als x=0. Er is lang over gediscussieerd of 00 ongedefinieerd is of een welgevormde uitdrukking. Voor alle positieve x is 0x=0.
In uitdrukkingen met limieten kan de grootheid 0/0 opduiken in de context van het aantonen van limieten van rationale functies zoals f(x)/g(x). In deze gevallen is 0/0 niet onbepaald, maar vertegenwoordigt het een onbepaalde vorm. Dit betekent niet dat de limiet onbepaald is, maar dat hij via een andere methode moet worden berekend, zoals het vinden van afgeleiden. Er bestaan enkele algebraïsche modellen waar deling door nul een gedefinieerde grootheid oplevert, zoals de projectief verlengde reële lijn of de sfeer van Riemann.
In de verzamelingenleer
In de verzamelingenleer komt het getal 0 overeen met de kardinaliteit de “lege verzameling” of de “nulverzameling” (gewoonlijk voorgesteld als {} of {∅}. De kardinaliteit van een verzameling is het aantal elementen in die verzameling als men geen sinaasappels heeft, dan heeft men een verzameling van 0 sinaasappels (een lege verzameling van sinaasappels).
Zero wordt in de verzamelingenleer vaak gebruikt als uitgangspunt om de rest van de natuurlijke getallen te construeren. Deze von Neumman constructies, genoemd naar de vermaarde polymaat John von Neumann construeert de natuurlijke getallen door 0={} te definiëren en een opvolgende functie S(a) = a ∪ {a} te definiëren. Het geheel van de natuurlijke getallen kan worden geconstrueerd uit de recursieve toepassingen van de opvolgingsfunctie, te beginnen met de lege verzameling:
0 = {}
1 = 0 ∪ {0} = {{}}
2 = 1 ∪ {1} = {0,1} = {{}, {{}}
3 = 2 ∪ {2} = {0, 1, 2} = {{}, {{}}, {{}}, {{}}}}
enzovoort. Volgens dit patroon kan men de volledige oneindige verzameling van de natuurlijke getallen construeren. Zo kan men zeggen dat elk natuurlijk getal correspondeert met de verzameling die alle natuurlijke getallen ervoor bevat.
In de natuurkunde
In de context van het doen van kwantitatieve metingen in de natuurkunde, wordt 0 beschouwd als de basislijn van waaruit alle andere metingen van eenheden worden gedaan. Heel vaak komt de basislijn van 0 overeen met een of andere fysisch significante variabele die op natuurlijke wijze te onderscheiden is van alle andere meetgrootheden.
In de schaal van Kelvin bijvoorbeeld, komt een temperatuur van 0 K overeen met absoluut 0 – de koudste temperatuur die fysisch mogelijk is. In de temperatuurschaal van Celsius wordt 0 °C gedefinieerd als het vriespunt van water bij atmosferische druk. In de context van dynamica en elektromagnetisme wordt een waarde van 0 gegeven aan de toestand waarin een systeem de kleinst mogelijke hoeveelheid potentiële energie heeft. Zo wordt aan de grondtoestand van een atoom, het laagst mogelijke energieniveau voor de elektronen in het atoom, vaak de waarde 0 toegekend.
Evenzo wordt in de context van de kinematica het referentiekader van waaruit waarnemingen van beweging worden gedaan gedefinieerd als hebbend een middelpunt dat ligt op de oorsprong van de coördinatenas in het punt (0, 0). In het geval van behouden grootheden, zoals massa-energie, momentum, en impulsmoment, is de totale hoeveelheid verandering van behouden grootheden in een geïsoleerd systeem altijd gelijk aan 0.
In de informatica
Computers slaan informatie op in de vorm van bits lange reeksen van 1-en en 0-en. In deze binaire weergave komt 0 overeen met een “uit”-positie en staat tegenover de “aan”-positie die wordt aangeduid met 1. Een waarde van 0 op een elektrisch circuit betekent dat het circuit uit is en geen elektrische stroom heeft. Op dezelfde manier wordt in veel computationele logica’s “0” gedefinieerd als het teken dat een valse waarheidswaarde vertegenwoordigt.
In computerdatabases worden de elementen van een matrix geteld met behulp van een op n gebaseerd telsysteem. Dit betekent dat voor een reeks met n elementen, de elementen indexen hebben beginnend met 0. Dus, een element met een indexnummer van 0 is eigenlijk het eerste element in de reeks, en een indexnummer van 1 komt overeen met het tweede element, enzovoort. In het algemeen heeft de n-de term van een reeks een indexnummer dat overeenkomt met n-1. Dit telsysteem kan verwarring veroorzaken bij nieuwe programmeurs die gewend zijn om intuïtief indexwaarden toe te kennen beginnend met 1.