De variantie is een getal dat aangeeft hoe ver een reeks getallen uit elkaar ligt.De variantie is identiek aan de kwadratische standaardafwijking en drukt dus “hetzelfde” uit (maar dan sterker).
Variantie – Voorbeeld
Een studie laat 100 mensen een eenvoudige snelheidstaak uitvoeren gedurende 80 trials. Van elke deelnemer worden dus 80 reactietijden (in seconden) geregistreerd. Een deel van deze gegevens wordt hieronder weergegeven.

In studies als deze zien we doorgaans dat mensen sneller worden naarmate ze de snelheidstaak vaker uitvoeren. Dat wil zeggen dat de gemiddelde reactietijd de neiging vertoont in de loop van de proeven af te nemen.
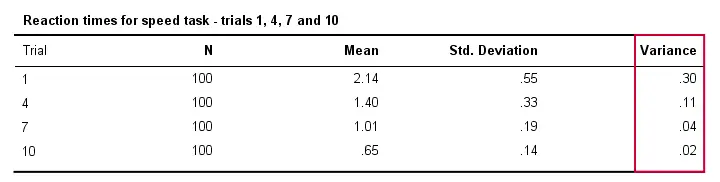
Ook zullen de reactietijden tussen verschillende mensen doorgaans minder verschillen naarmate zij de taak vaker uitvoeren. Technisch gesproken zeggen we dat de variantie afneemt over de proeven. De onderstaande tabel illustreert dit voor de proeven 1,4,7 en 10.
Variantie en Histogram
Een goede manier om de gegevens uit onze vorige tabel te visualiseren is een histogram voor elke proef. De onderstaande figuur illustreert dat de deelnemers in de loop van de proeven sneller zijn geworden; van proef 1 tot proef 10 bewegen de histogrambalken naar links, in de richting van 0 seconden.
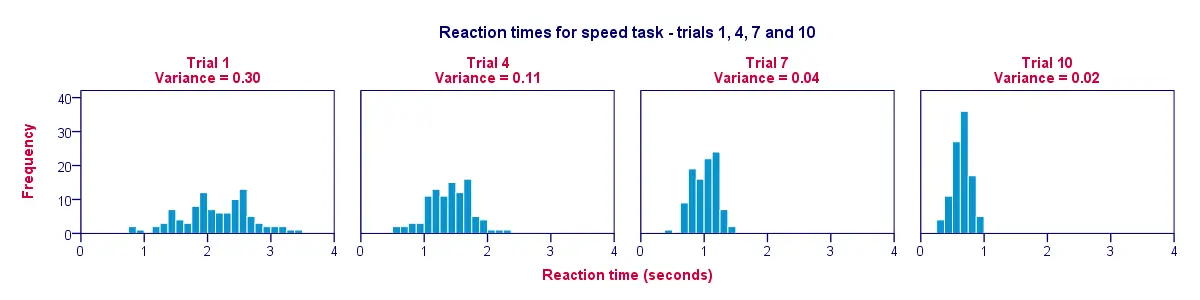
Een tweede bevinding is dat de histogrammen smaller (en dus hoger) worden naarmate we van proef 1 naar proef 10 gaan; dit illustreert dat de reactietijden tussen onze deelnemers steeds minder verschillen naarmate het experiment vordert. De variantie neemt af over de proeven.
Variantie – Populatieformule
Een basisformule voor het berekenen van de variantie is
$$S^2 = \frac{\sum(X – \overline{X})^2}{n}$
We raden je aan te proberen te begrijpen wat deze formule doet, want dit helpt veel bij het begrijpen van ANOVA (= analyse van variantie). We zullen het daarom demonstreren aan de hand van een handvol gegevens.
Variantie – GoogleSheets
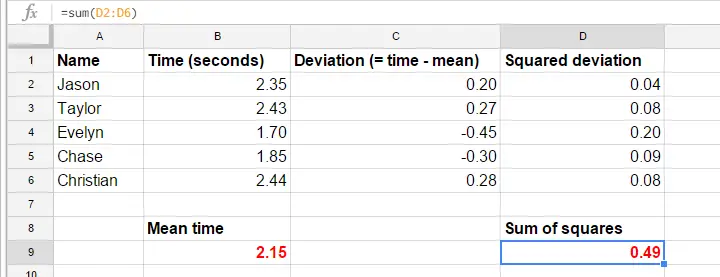
Voor de eenvoud beperken we onze gegevens tot de eerste proef voor de eerste 5 deelnemers. Deze 5 reactietijden – en een handmatige berekening van hun variantie – staan in dit GoogleSheet.
Variantie – Berekeningsstappen
De formules in het GoogleSheet laten precies zien hoe je een variantie berekent. De basisstappen zijn
- bereken de gemiddelde reactietijd (2,15);
- bereken afwijkingsscores (reactietijd min gemiddelde reactietijd);
- bereken gekwadrateerde afwijkingsscores;
- tel gekwadrateerde afwijkingsscores bij elkaar op. Het resultaat (0,49) is een som van kwadraten, de belangrijkste bouwsteen van ANOVA;
- deel de som van kwadraten door het aantal waarnemingen (5 reactietijden).
Als alternatief kunt u een variantie berekenen door =VARP(B2:B6) in een of andere cel te typen (B2:B6 zijn de cellen waarin onze 5 reactietijden staan). VARP is een afkorting voor “variantie populatie”. OpenOffice en MS Excel bevatten soortgelijke formules.
Variantie – Steekproefformule
Gelijk aan de standaardafwijking zal, als onze gegevens een eenvoudige aselecte steekproef zijn uit een veel grotere populatie, de bovengenoemde formule de populatievariantie systematisch onderschatten. In dat geval gebruiken we een iets andere formule:
$$S^2 = \frac{(X_i – \overline{X})^2}{n – 1}$$
Welke formule we gebruiken hangt dus af van onze gegevens: bevatten ze de hele populatie die we willen onderzoeken of zijn ze slechts een steekproef uit deze populatie?
Omdat onze 100 deelnemers duidelijk een steekproef zijn, zullen we de steekproefformule gebruiken. In GoogleSheets geeft het intikken van =VAR(B2:B6) in een of andere cel de steekproefvariantie.
Variantie in SPSS
Voor zover wij weten ontbreekt de formule voor de populatievariantie volledig in SPSS en wij beschouwen dit als een ernstige tekortkoming. In plaats daarvan gebruikt SPSS altijd de steekproefformule. Dit geldt zowel voor de variantie tussen proefpersonen (besproken in deze tutorial) als voor de variantie binnen proefpersonen. Relevante uitvoer wordt hieronder getoond.

Met betrekking tot deze uitvoertabel, merk ook op dat de variantie inderdaad de gekwadrateerde standaardafwijking is (afgezien van de afronding).
Met betrekking tot de variantie, dat is het zo’n beetje. We hopen dat je deze tutorial nuttig vond om te begrijpen wat een variantie is.