Ongewenste convolutie is een inherent probleem bij de overdracht van analoge informatie. Bijvoorbeeld, al het volgende kan worden gemodelleerd als een convolutie: beeldonscherpte in een trillende camera, echo’s in telefoongesprekken over lange afstand, de eindige bandbreedte van analoge sensoren en elektronica, enz. Deconvolutie is het proces waarbij een signaal wordt gefilterd om een ongewenste convolutie te compenseren. Het doel van deconvolutie is het signaal te reconstrueren zoals het bestond vóór deconvolutie plaatsvond. Hiervoor is het gewoonlijk noodzakelijk dat de kenmerken van deconvolutie (d.w.z. de impuls- of frequentierespons) bekend zijn. Dit kan worden onderscheiden van blinde deconvolutie, waarbij de kenmerken van de parametrische convolutie niet bekend zijn. Blinde deconvolutie is een veel moeilijker probleem dat geen algemene oplossing heeft, en de aanpak moet worden toegesneden op de specifieke toepassing.
Deconvolutie is bijna onmogelijk te begrijpen in het tijdsdomein, maar vrij eenvoudig in het frequentiedomein. Elke sinusoïde waaruit het oorspronkelijke signaal is opgebouwd, kan in amplitude en/of fase worden veranderd terwijl het door de ongewenste convolutie gaat. Om het originele signaal te extraheren, moet het deconvolutiefilter deze amplitude- en faseveranderingen ongedaan maken. Bijvoorbeeld
, indien de convolutie de amplitude van een sinusoïde met 0,5 wijzigt met een faseverschuiving van 30 graden, moet het deconvolutiefilter de sinusoïde met 2,0 versterken met een faseverschuiving van -30 graden.
Het voorbeeld dat wij zullen gebruiken om de deconvolutie te illustreren is een gammastralingsdetector. Zoals geïllustreerd in fig. 17-3, bestaat dit apparaat uit twee delen, een scintillator en een lichtdetector. Een scintillator is een speciaal soort doorzichtig materiaal, zoals natriumjodide of bismutgermanaat. Deze verbindingen zetten de energie van elke gammastraal om in een korte uitbarsting van zichtbaar licht. Dit licht
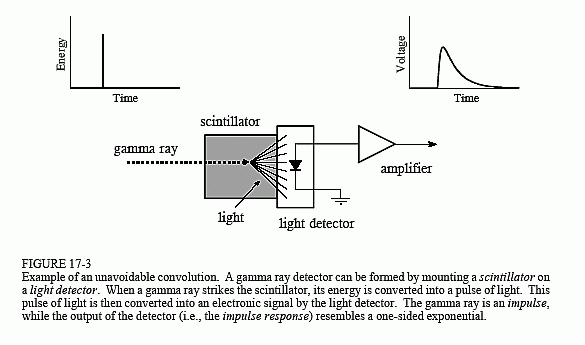
wordt dan omgezet in een elektronisch signaal door een lichtdetector, zoals een fotodiode of een fotomultiplicatorbuis. Elke door de detector geproduceerde puls lijkt op een eenzijdige exponentiaal, met enige afronding van de hoeken. Deze vorm wordt bepaald door de kenmerken van de gebruikte scintillator. Wanneer een gammastraal zijn energie in de scintillator deponeert, worden nabijgelegen atomen tot een hoger energieniveau geëxciteerd. Deze atomen deexciteren willekeurig en produceren elk een enkel foton zichtbaar licht. Het nettoresultaat is een lichtpuls waarvan de amplitude over een paar honderd nanoseconden afneemt (voor natriumjodide). Aangezien de aankomst van elke gammastraal een impuls is, is de uitgangsimpuls van de detector (d.w.z. de eenzijdige xponentiaal) de impulsrespons van het systeem.
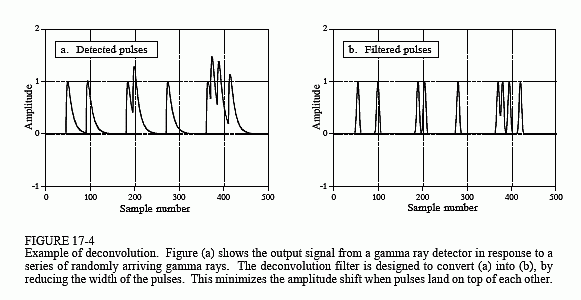
Figuur 17-4a toont pulsen die door de detector worden opgewekt als reactie op willekeurig binnenkomende gammastralen. De informatie die wij uit dit uitgangssignaal willen halen is de amplitude van elke puls, die evenredig is met de energie van de gammastraal die de puls heeft opgewekt. Dit is nuttige informatie omdat de energie interessante dingen kan vertellen over waar de gammastraal is geweest. Het kan bijvoorbeeld medische informatie over een patiënt opleveren, de leeftijd van een ver sterrenstelsel aangeven, een bom in vliegtuigbagage opsporen, enz.
Alles zou mooi zijn als er maar af en toe een gammastraal zou worden gedetecteerd, maar dat is meestal niet het geval. Zoals in (a) te zien is, kunnen twee of meer pulsen elkaar overlappen, waardoor de gemeten amplitude verschuift. Een oplossing voor dit probleem is het deconvolveteren van het uitgangssignaal van de detector, waardoor de pulsen smaller worden en er minder opeenstapeling optreedt. Idealiter zouden we willen dat elke puls lijkt op de oorspronkelijke impuls. Zoals u wellicht vermoedt, is dit niet mogelijk en moeten wij genoegen nemen met een puls die eindig is, maar aanzienlijk korter dan de gedetecteerde puls. Dit doel wordt geïllustreerd in fig. 17-4b.
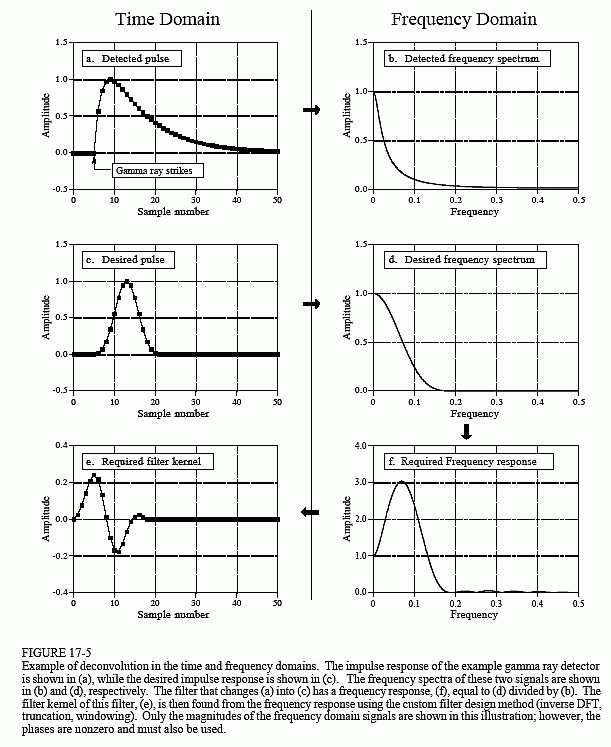
Ondanks het feit dat de informatie van het detectorsignaal in het tijdsdomein is gecodeerd, moet een groot deel van onze analyse in het frequentiedomein worden uitgevoerd, waar het probleem gemakkelijker te begrijpen is. Figuur 17-5a is het signaal dat door de detector wordt geproduceerd (iets wat we weten). Figuur (c) is het signaal dat we willen hebben (ook iets dat we weten). Deze gewenste puls is willekeurig gekozen om dezelfde vorm te hebben als een Blackman-venster, met een lengte van ongeveer een derde van die van de oorspronkelijke puls. Ons doel is een filterkernel, (e), te vinden die, wanneer hij wordt geconvolveerd met het signaal in (a), het signaal in (c) oplevert. In de vorm van een vergelijking: als a * e = c, en gegeven a en c, vind dan e.
Als deze signalen werden gecombineerd door optellen of vermenigvuldigen in plaats van door convolutie, zou de oplossing gemakkelijk zijn: aftrekken wordt gebruikt om “op te tellen” en delen wordt gebruikt om “te vermenigvuldigen”. Convolutie is anders; er is geen eenvoudige omgekeerde operatie die “deconvolutie” kan worden genoemd. Convolutie is te rommelig om ongedaan te worden gemaakt door directe manipulatie van de tijddomein-signalen.
Gelukkig genoeg is dit probleem eenvoudiger in het frequentiedomein. Denk eraan, convolutie in het ene domein komt overeen met vermenigvuldiging in het andere domein. Nogmaals verwijzend naar de signalen in fig. 17-5: als b × f = d, en gegeven b en d, vind dan f. Dit is een eenvoudig op te lossen probleem: de frequentierespons van het filter, (f), is het frequentiespectrum van de gewenste puls, (d), gedeeld door het frequentiespectrum van de gedetecteerde puls, (b). Aangezien de gedetecteerde puls asymmetrisch is, zal deze een fase hebben die niet nul is. Dit betekent dat een complexe deling moet worden gebruikt (dat wil zeggen, een magnitude & fase gedeeld door een andere magnitude & fase). Voor het geval u het vergeten bent: in hoofdstuk 9 wordt beschreven hoe een complexe deling van het ene spectrum door het andere moet worden uitgevoerd. De vereiste filterkernel, (e), wordt dan uit de frequentierespons gevonden met behulp van de aangepaste filtermethode (IDFT, verschuiven, afkappen, &vermenigvuldigen met een venster).
Er zijn grenzen aan de verbetering die deconvolutie kan opleveren. Met andere woorden, als je hebzuchtig wordt, zullen dingen uit elkaar vallen. Hebberig worden betekent in dit voorbeeld dat je probeert de gewenste puls te smal te maken. Laten we eens kijken wat er dan gebeurt. Als de gewenste puls smaller wordt gemaakt, moet het frequentiespectrum meer hoogfrequente componenten bevatten. Aangezien deze hoogfrequente componenten een zeer lage amplitude hebben in de gedetecteerde puls, moet het filter een zeer hoge versterking hebben bij deze frequenties. Zo blijkt uit (f) dat sommige frequenties met een factor drie moeten worden vermenigvuldigd om de gewenste puls in (c) te verkrijgen. Indien de gewenste puls smaller wordt gemaakt, zal de versterking van het deconvolutiefilter bij hoge frequenties nog groter zijn.
Het probleem is dat kleine fouten in deze situatie zeer onvergeeflijk zijn. Als bijvoorbeeld een bepaalde frequentie met 30 wordt versterkt, terwijl er maar 28 nodig is, zal het gedeconvolueerde signaal waarschijnlijk een puinhoop zijn. Wanneer de deconvolutie op een hoger prestatieniveau wordt gebracht, moeten de kenmerken van de ongewenste convolutie met grotere nauwkeurigheid en precisie worden begrepen. In toepassingen in de echte wereld zijn er altijd onbekenden, veroorzaakt door schurken als: elektronische ruis, temperatuurafwijking, variatie tussen apparaten, enz. Deze onbekenden stellen een grens aan hoe goed de deconvolutie zal werken.
Zelfs als de ongewenste convolutie perfect wordt begrepen, is er nog een factor die de prestaties van de deconvolutie beperkt: ruis. Zo hebben de meeste ongewenste convoluties de vorm van een laagdoorlaatfilter, waardoor de amplitude van de hoge frequentiecomponenten in het signaal wordt gereduceerd. Deconvolutie corrigeert dit door deze frequenties te versterken. Indien de amplitude van deze componenten echter onder de inherente ruis van het systeem daalt, gaat de in deze frequenties vervatte informatie verloren. Geen enkele signaalverwerking kan die terugwinnen. Het is voor altijd weg. Adios! Vaarwel. Sayonara! Proberen deze gegevens terug te halen zal alleen de ruis versterken. In het uiterste geval kan de amplitude van sommige frequenties volledig tot nul worden gereduceerd. Hierdoor wordt niet alleen de informatie uitgewist, maar wordt ook geprobeerd het deconvolutiefilter op deze frequenties een oneindige versterking te geven. De oplossing: ontwerp een minder agressief deconvolutiefilter en/of stel grenzen aan de hoeveelheid versterking die is toegestaan op elk van de frequenties.
Hoe ver kun je gaan? Hoe gulzig is te gulzig? Dat hangt helemaal af van het probleem dat u aanpakt. Als het signaal zich goed gedraagt en weinig ruis vertoont, kan waarschijnlijk een aanzienlijke verbetering worden bereikt (denk aan een factor 5-10). Als het signaal in de loop van de tijd verandert, niet bijzonder goed begrepen wordt, of ruis bevat, zal het lang niet zo goed gaan (denk aan een factor 1-2). Succesvolle deconvolutie vereist veel testen. Als het op een bepaald niveau werkt, probeer dan verder te gaan; je zult weten wanneer het uit elkaar valt. Geen enkele hoeveelheid theoretisch werk zal je in staat stellen dititeratieve proces te omzeilen.
Deconvolutie kan ook worden toegepast op frequentiedomein-gecodeerde signalen. Een klassiek voorbeeld is de restauratie van oude opnamen van de beroemde operazanger Enrico Caruso (1873-1921). Deze opnamen zijn gemaakt met naar moderne maatstaven zeer primitieve apparatuur. Het grootste probleem zijn de trillingen van de lange buisvormige hoorn die werd gebruikt om het geluid op te vangen. Telkens wanneer de zanger een van deze resonantiefrequenties raakt, neemt de luidheid van de opname abrupt toe. Digitale deconvolutie heeft de subjectieve kwaliteit van deze opnamen verbeterd door
de luide plekken in de muziek te verminderen. Wij beschrijven hier alleen de algemene methode; voor een gedetailleerde beschrijving wordt verwezen naar het oorspronkelijke artikel: T. Stockham, T. Cannon, andR. Ingebretsen, “Blind Deconvolution Through Digital Signal Processing”,Proc. IEEE, vol. 63, Apr. 1975, pp. 678-692.
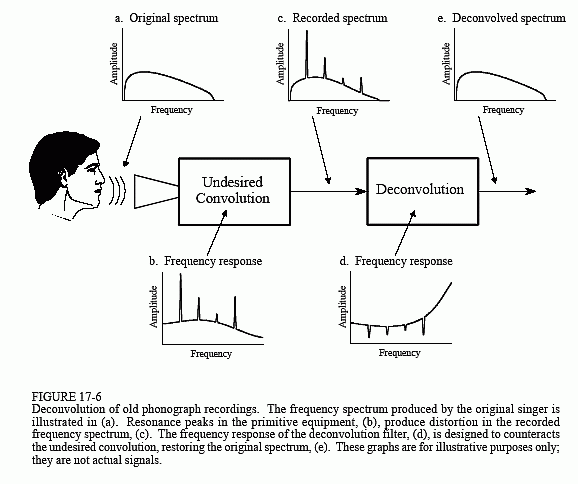
Figuur 17-6 toont de algemene aanpak. Het frequentiespectrum van het oorspronkelijke audiosignaal is afgebeeld in (a). Figuur (b) toont de frequentierespons van de opnameapparatuur, een betrekkelijk vloeiende curve met uitzondering van enkele scherpe resonantiepieken. Het spectrum van het opgenomen signaal, getoond in (c), is gelijk aan het ware spectrum, (a), vermenigvuldigd met de ongelijke frequentierespons, (b). Het doel van de deconvolutie is de ongewenste deconvolutie tegen te gaan. Met andere woorden, de frequentierespons van het deconvolutiefilter,(d), moet de inverse zijn van (b). Dat wil zeggen dat elke piek in (b) wordt geannuleerd door een overeenkomstige dip in (d). Als dit filter perfect was ontworpen, zou het resulterende signaal een spectrum, (e), hebben dat identiek is aan dat van het origineel.
Hier zit het addertje onder het gras: de oorspronkelijke opnameapparatuur is al lang weggegooid, en de frequentierespons, (b), is een mysterie. Met andere woorden, dit is een blinddeconvolutie probleem; gegeven alleen (c), hoe kunnen we bepalen (d)?
Blinde deconvolutieproblemen worden gewoonlijk aangepakt door een schatting of aanname te doen over de onbekende parameters. In dit voorbeeld wordt aangenomen, dat het gemiddelde spectrum van de oorspronkelijke muziek overeenkomt met het gemiddelde spectrum van dezelfde muziek, uitgevoerd door een hedendaagse zanger met moderne apparatuur. Het gemiddelde spectrum wordt gevonden met behulp van de technieken van hoofdstuk 9: breek het signaal op in een groot aantal segmenten, neem de DFT van elk segment, zet het om in polaire vorm en neem dan het gemiddelde van de magnitudes. In het eenvoudigste geval wordt de onbekende frequentierespons genomen als het gemiddelde spectrum van de oude opname, gedeeld door het gemiddelde spectrum van de moderne opname. (De door Stockham e.a. gebruikte methode is gebaseerd op een meer verfijnde techniek, homomorfe verwerking genoemd, die een betere schatting van de kenmerken van het opnamesysteem oplevert).