Hoe de spanning te berekenen in touwen die een voorwerp ophangen

We kunnen in de illustratie hieronder zien dat de kracht, F, die nodig is om het voorwerp op te tillen gelijk is aan het gewicht, W, van het voorwerp. Dit idee is het fundamentele concept dat ten grondslag ligt aan onze formule van de spankracht. Hieronder is ook het vrij-lichaam diagram van het voorwerp te zien dat de trekkrachten, T, toont die in de snaar werken. Zoals u kunt zien, komen de spankrachten in paren en in tegengestelde richtingen:

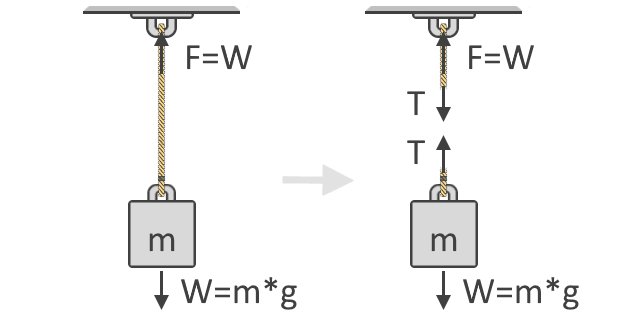
Volgens de tweede bewegingswet van Newton kunnen we de som van de krachten uitdrukken met behulp van het vrij-lichaamdiagram van het voorwerp, zoals rechts in de bovenstaande illustratie. We gebruiken vrij-lichaam diagrammen om de verschillende richtingen en groottes van de krachten die op een lichaam werken te laten zien. In evenwicht moeten al deze krachten gelijk zijn aan nul. Als we alle opwaartse krachten als positief beschouwen en de neerwaartse als negatief, luidt onze vergelijking:

ΣF = 0 = T + (-W)
T = W
waarbij het gewicht, W, negatief wordt omdat het naar beneden is gericht. Door W naar de andere kant van de vergelijking te transponeren, kunnen we nu zien dat de trekkracht in het touw gelijk is aan het gewicht van het voorwerp dat het draagt, zoals ook hierboven is aangetoond.

Als we meer touwen gebruiken om het voorwerp op te tillen, wordt de totale trekkracht over de touwen verdeeld. De trekkracht in elk touw hangt af van de hoek ervan ten opzichte van de richting van de kracht die het tegenwerkt. Laten we, om dit beter te begrijpen, een ander vrij-lichaamsdiagram bekijken van een voorwerp dat aan twee touwen hangt, zoals hieronder:

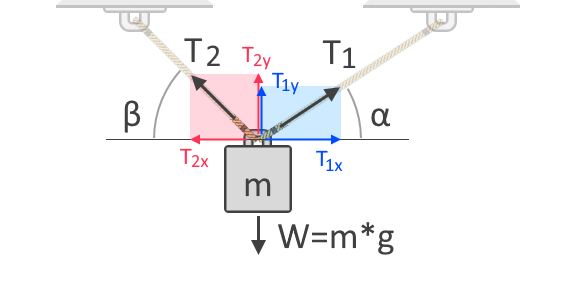
In het hierboven getoonde vrij-lichaamsdiagram zien we de horizontale en verticale componenten van de trekkrachten, T₁, en T₂. Krachten zijn vectoren, wat betekent dat ze altijd zowel een grootte als een richting hebben. Zoals alle vectoren kunnen krachten worden uitgedrukt in deze componenten, die de invloed van de kracht langs de horizontale en verticale assen weergeven. T₁ₓ en T₂ₓ zijn de verticale componenten van respectievelijk T₁ en T₂. Anderzijds zijn T₁ᵧ en T₂ᵧ de verticale componenten van dezelfde krachten, respectievelijk. Aangezien de zwaartekracht in de verticale as op het voorwerp werkt, moeten we de verticale componenten van de spankrachten als volgt in aanmerking nemen voor onze sommering van krachten:

ΣF = 0 = T₁ᵧ + T₂ᵧ + (-W)
W = T₁ᵧ + T₂ᵧ

Omdat we ook de hoeken van de spankrachten kennen, kunnen we T₁ᵧ en T₂ᵧ uitdrukken in termen van respectievelijk T₁ en T₂, met behulp van goniometrische functies:

T₁ᵧ = T₁ * sin(α)
T₂ᵧ = T₂ * sin(β)
W = T₁ * sin(α) + T₂ * sin(β)

We kunnen ook zeggen dat, wil het systeem in evenwicht zijn, het voorwerp niet horizontaal of langs de x-as mag bewegen. Daarom moeten de horizontale componenten van T₁ en T₂ dan gelijk zijn aan nul. Ook kunnen we met behulp van goniometrie T₁ₓ en T₂ₓ uitdrukken in termen van T₁ en T₂, respectievelijk:

T₁ₓ = T₂ₓ
T₁ * cos(α) = T₂ * cos(β)

Als we beide zijden delen door cos(α), krijgen we een vergelijking waarin T₁ wordt uitgedrukt in termen van T₂ en de hoeken:

T₁ = T₂ * cos(β) / cos(α)

We kunnen dan deze vergelijking gebruiken om voor T₂ op te lossen door T₂ * cos(β) / cos(α) als T₁ te substitueren in onze sommatie van krachten vergelijking, zoals hieronder getoond:

W = T₁ * sin(α) + T₂ * sin(β)
W = T₂ * * sin(α) + T₂ * sin(β)
W = T₂ *
T₂ = W /

Ten slotte, als we deze hele vergelijking vermenigvuldigen met cos(β) / cos(α) zoals we hebben afgeleid in de waarde van T₁ in termen van T₂, en dan alles vereenvoudigen, krijgen we deze vergelijking:

T₁ = W / *
T₁ = W / *
T₁ = W /

Nu hoef je alleen nog maar de hoeken van de spankabels ten opzichte van de horizontaal te weten. Als er een hoek met de verticaal is gegeven, trek je deze hoek gewoon af van 90°. Op die manier verkrijgt men de hoek met het horizontale vlak. Als je echter andere waarden van hoeken krijgt die groter kunnen zijn dan 90° of zelfs 180°, kun je misschien onze referentiehoekcalculator raadplegen om je te helpen de hoek te bepalen die je nodig hebt. Na het bepalen van de waarden voor de variabelen in onze spankrachtformules, kunnen we nu de spankrachten oplossen.