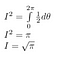Lord Kelvin schreef over deze integraal: “Een wiskundige is iemand voor wie dat net zo vanzelfsprekend is als dat twee keer twee vier is voor jou.”
Geniet 😉
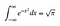
OK, dus ik ga ervan uit dat je wat basiskennis hebt van integreren en differentiëren. Het volgende zal wat intuïtie toevoegen aan slimme trucs die later komen. Maak je geen zorgen als het soms wat verbijsterend is, probeer gewoon een gevoel te krijgen voor wat er gebeurt.
De strategie hier zal zijn om een slimme substitutie uit te voeren. Maar we doen een substitutie in twee variabelen. U kunt het huidige probleem zien als het berekenen van de oppervlakte onder een kromme
Maar we zullen laten zien dat het probleem kan worden omgezet in een probleem van het berekenen van een volume.
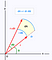
Om het volume te berekenen, gebruiken we een iets andere formule voor het veranderen van variabelen dan wat je in normale integralen gebruikt. We zullen polaire coördinaten gebruiken. Dit drukt de x- en y-coördinaten uit in termen van hun straal en hun hoek. Geogebra heeft hier een leuke interactieve manier om dit te zien

Dan gebruiken we de magische verandering van basisformule voor poolcoördinaten.
Bij het berekenen van de oppervlakte onder de kromme, hadden we het element ‘dx’ dat een kleine afstand langs de x-as voorstelt. Bij het berekenen van een volume hebben we dx dy, dat is als een kleine rechthoek met zijde lengte dx en dy. Vervolgens gebruiken we deze grondvlakken om een reeks hokjes te maken die het volume schatten. Dit is het gemakkelijkst te zien met de onderstaande visualisatie. De integraal is de limiet van deze benaderingen.
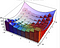
Wanneer we in plaats daarvan het poolcoordinatenstelsel gebruiken, hebben we er een iets ander oppervlakte-element onder. Hieronder is dA het oppervlakte-element. Met kleine veranderingen in de hoek en de straal kan dit oppervlakte-element steeds beter benaderd worden door een rechthoek met zijden respectievelijk dr en r*dtheta. Als je een beetje handig bent met meetkunde, wordt voor kleine theta sin(theta) heel goed benaderd door theta en dan kun je onderstaand resultaat bewijzen.
Oplossen van de integraal
Eerst geven we een naam aan onze integraal. We noemen hem I.
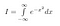
Merk op dat x slechts een ‘dummy variabele’ is. Het gebied bestaat ongeacht welke variabelenaam we gebruiken. We kunnen dus ook de volgende twee vergelijkingen schrijven
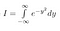
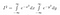
Nu, aangezien I gewoon een constante is, zij het een waarvan we de waarde nog niet kennen, kunnen we onze normale regels gebruiken om een constante binnen een integraal te brengen
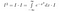
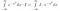
Tot nu toe hebben we nog niet veel inhoudelijks gedaan. Nu denken we goed na over wat de integraal betekent. We nemen integralen van functies. Als twee functies overal dezelfde waarde hebben, zijn ze hetzelfde, en hebben ze dezelfde oppervlakte. Met dat in gedachten kunnen we de volgende bewerkingen uitvoeren, als we I*exp(-x²) beschouwen als een functie van x, d.w.z. iets dat waarden van x als invoer neemt, en een getal als uitvoer geeft.
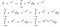
Ok, dat was een heleboel om te verwerken. In de eerste regel hebben we I gewoon herschreven in zijn integrale vorm met een andere variabele naam. In de tweede regel, waarbij we I*exp(-x²) als een functie behandelen, realiseerden we ons dat we de exp(-x²) binnen de dy-integraal kunnen brengen, en dat dit nog steeds dezelfde uitvoerwaarde zou geven voor elke invoerwaarde van x. Tenslotte hebben we de regels van de exponentiatie gebruikt.
Wanneer we dit volledig uitschrijven, hebben we nu
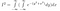
Nog komt het killer inzicht. Hierboven hebben we gerommeld met variabele namen en hoe we een functie moeten voorstellen. Nu verleggen we ons perspectief: deze uitdrukking stelt ook de integraal voor van exp(-(y²+x²)) over het gehele 2D-vlak, met gebiedselement dA = dx dy. D.w.z. dx dy is een kleine rechthoek op een vlak, en exp(-(y²+x²)) is de hoogte boven die rechthoek.
Volgende gebruiken we de polaire coördinaten inzichten van eerder
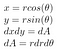
Als sin² + cos² = 1, na alles in te pluggen, krijgen we
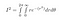
r loopt van 0 tot oneindig en theta loopt van 0 tot 2*pi, omdat dit het hele 2D-vlak bestrijkt: elk punt heeft een straal kleiner dan oneindig, en een hoek tussen 0 en 2pi radialen.
We kunnen de binnenintegraal evalueren met behulp van de kettingregel
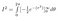
En, in het beloofde land bevinden we ons nu: