Als licht door een materiaalstructuur wordt weerkaatst of doorgelaten, treedt er een verandering in polarisatie op. Ellipsometrie meet deze respons die afhangt van optische eigenschappen en dikte van individuele materialen. Ellipsometrie wordt hoofdzakelijk gebruikt om optische constanten en filmdikte te bepalen, maar ook om samenstelling, kristalliniteit, ruwheid, doteringsconcentratie en andere materiaaleigenschappen te karakteriseren die in verband worden gebracht met een verandering in optische respons.

Toepassingsgebieden zijn fundamenteel onderzoek in de natuurwetenschappen, halfgeleider- en gegevensopslagoplossingen, platte beeldschermen, communicatie, biosensoren, en optische coatingindustrieën. Ellipsometrie heeft ook de flexibiliteit om de meeste materiaalsoorten te meten: diëlektrica, halfgeleiders, metalen, supergeleiders, organische stoffen, biologische coatings en composieten.

Gepolariseerd licht definitie

Licht kan worden omschreven als een elektromagnetische golf die door de ruimte reist. De wijze waarop het veld van een elektromagnetische golf zich gedraagt in relatie tot ruimte en tijd wordt polarisatie genoemd. Licht wordt als ongepolariseerd beschouwd wanneer de oriëntatie en de fase ervan volkomen willekeurig zijn. Ellipsometrie meet echter gepolariseerd licht – een elektrisch veld dat een specifiek pad volgt en op elk gegeven punt een duidelijke vorm heeft. Een elektromagnetische golf die in z-richting reist, kan worden beschreven door zijn x- en y-componenten, omdat zijn elektrisch veld altijd loodrecht op de voortplantingsrichting staat. Wanneer twee orthogonale lichtgolven in fase zijn, is het resulterende licht lineair gepolariseerd. De oriëntatie wordt bepaald door de relatieve amplitudes. Het licht wordt als circulair gepolariseerd beschouwd als de orthogonale golven 90° uit fase zijn en dezelfde amplitude hebben. De meest voorkomende polarisatie is elliptisch en combineert orthogonale golven van willekeurige amplitude en fase. Dit is waar ellipsometrie zijn naam aan ontleent.

Verschillende soorten polarisatie:

Lineair

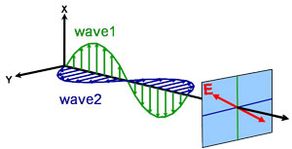
Circulair

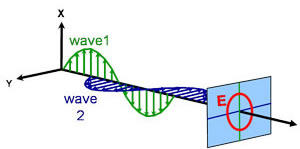
Elliptisch

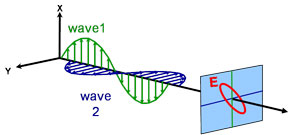
Optische eigenschappen

De optische eigenschappen die bepalen hoe licht op een materiaal inwerkt, worden door twee waarden beschreven. Ze worden meestal voorgesteld als een complex getal. De complexe brekingsindex (ñ) bestaat uit de index (n) en een extinctiecoëfficiënt (k):

De optische eigenschappen kunnen ook worden weergegeven als een complexe diëlektrische functie:

met het volgende verband tussen conventies:

De index geeft de fasesnelheid van licht weer wanneer het zich in een materiaal beweegt, vergeleken met de lichtsnelheid wanneer het zich in vacuüm beweegt, c:

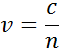
Wanneer het licht materiaal met een hogere index binnengaat, wordt het langzamer. Aangezien de frequentie van de lichtgolven niet verandert, wordt de golflengte korter. Het verlies van golfenergie aan het materiaal wordt beschreven door de extinctiecoëfficiënt die als volgt gerelateerd is aan de absorptiecoëfficiënt:

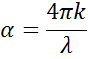
Volgens de wet van Beer verliest licht aan intensiteit in een absorberend materiaal. De extinctiecoëfficiënt geeft aan hoe snel licht in een materiaal verdwijnt.

Figuur 4 toont een lichtgolf die door twee verschillende materialen met verschillende eigenschappen reist alvorens naar de omgeving terug te keren.

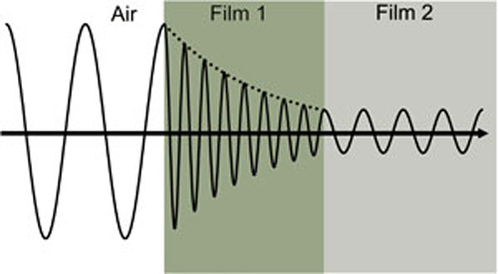
Figuur 4: Lichtgolf die vanuit de lucht in de absorberende Film 1 en vervolgens in de transparante Film 2 reist. Fasesnelheid en golflengte veranderen in beide materialen, afhankelijk van de brekingsindex (Film 1: n=4, Film 2: n=2).

De golflengte bepaalt de optische constanten. Figuur 5 toont de optische constanten voor TiO2 van UV tot IR. Wegens verschillende processen die energie aan de lichtgolf onttrekken, treedt absorptie (k>0) op in zowel UV als IR. IR-absorptie wordt gewoonlijk veroorzaakt door moleculaire of fonontrillingen of vrije-carriers. UV-absorptie vindt meestal plaats door elektronische overgangen, waarbij lichtenergie elektronen exciteert tot verhoogde toestanden. Figuur 5 toont aan dat hypothetische of reële optische constanten niet onafhankelijk zijn, maar mathematisch met elkaar verbonden via Kramers-Kronig relaties.

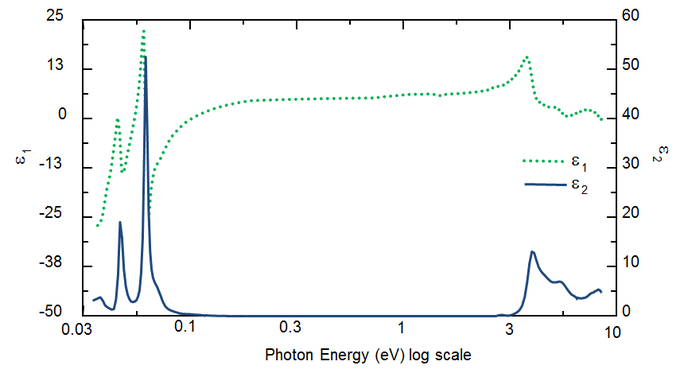
Figuur 5: Complexe diëlektrische functie voor TiO2 film met golflengten van IR (kleine eV) tot UV (hoge eV).

Licht en materiaalinteractie

Wanneer licht interageert met een materiaal, leidt dit tot randvoorwaarden aan het grensvlak. Hierbij moet altijd aan de vergelijkingen van Maxwell worden voldaan. De onderstaande figuur toont hoe invallend licht reflecteert en breekt aan het grensvlak. De hoek tussen de invallende straal en de normaal van het materiaal (θi) zal gelijk zijn aan de gereflecteerde hoek (θr). Licht dat een materiaal binnenkomt, wordt gebroken onder een hoek θt die gegeven wordt door:

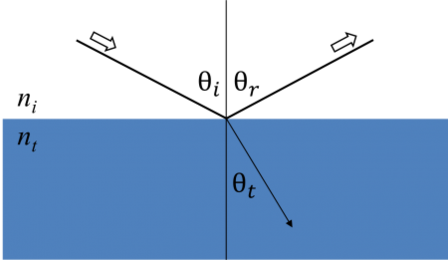
Figuur 6: Licht weerkaatst en breekt volgens de wet van Snell.

Op elk grensvlak wordt een deel van het licht gereflecteerd, terwijl de rest onder de brekingshoek doorgelaten wordt. Afhankelijk van de randvoorwaarden gelden verschillende oplossingen voor elektrische velden evenwijdig aan en loodrecht op het oppervlak van het proefstuk. Het licht kan dus worden gescheiden in orthogonale componenten ten opzichte van het invalsvlak (p- en s-gepolariseerd). Beide componenten kunnen afzonderlijk worden berekend. Zo beschreef Fresnel de hoeveelheid licht die wordt gereflecteerd en doorgelaten op een grensvlak tussen materialen:

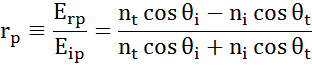
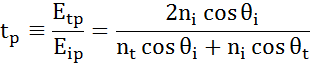
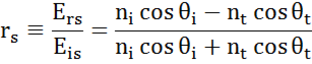
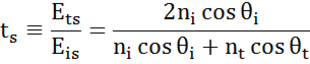
Meerdere grensvlakken met de juiste Fresnel reflectie- en transmissiecoëfficiënten komen voor bij dunne film- en meerlaagse structuren. Om de gereflecteerde of uitgezonden bundel correct te bepalen, moet de relatieve fase van elke lichtcomponent worden bijgehouden. De dikte van de filmfase wordt dus als volgt bepaald:

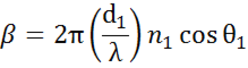
Wanneer verschillende lichtgolven elkaar overlappen, treedt interferentie op die afhankelijk is van de relatieve fase van elke afzonderlijke lichtgolf. De onderstaande figuur toont de combinatie van lichtgolven in de gereflecteerde bundel en hun overeenkomstige Fresnel-berekeningen.

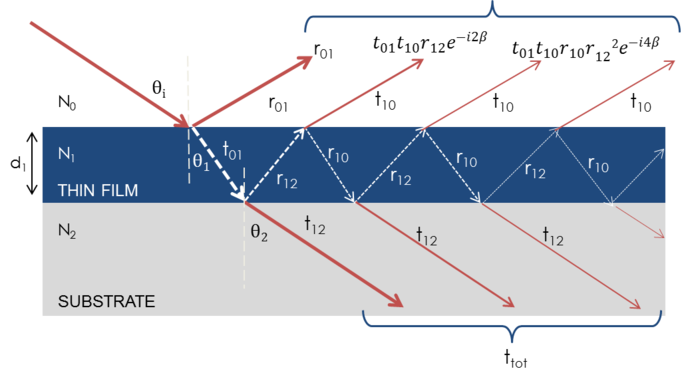
Figuur 7: Licht reflecteert en breekt op elk afzonderlijk grensvlak, wat leidt tot meervoudige bundels in een dunne film. Straalinterferentie hangt af van de relatieve fase en amplitude van de elektrische velden. De reactie van de bundel kan worden berekend met de reflectie- en transmissiecoëfficiënten van Fresnel.

Metingen

Ellipsometrie meet hoofdzakelijk hoe p- en s-componenten ten opzichte van elkaar reageren tijdens reflectie of transmissie. Een referentiestraal maakt dus altijd deel uit van het experiment. Een bekende polarisatie wordt door het monster gereflecteerd of uitgezonden en de uitgangspolarisatie wordt gemeten. De polarisatieverandering is de ellipsometermeting:

Figuur 6 toont een typische ellipsometermeting van een monster. Het lineaire invallende licht heeft zowel p- als s-componenten. Het gereflecteerde licht vertoont zowel amplitude- als faseveranderingen voor zowel p- als s- gepolariseerd licht. Deze veranderingen worden gemeten door middel van ellipsometrie.

Om ellipsometriegegevens te verzamelen is het volgende nodig: lichtbron, polarisatiegenerator, monster, polarisatie-analysator, en detector. Zowel de polarisatiegenerator als de analyzer bestaan uit optische onderdelen die de polarisatie manipuleren: compensatoren, polarisatoren, en fasemodulatoren. Typische ellipsometerconfiguraties omvatten een roterende analysator (RAE), een roterende polarisator (RPE), een roterende compensator (RCE), en een fasemodulatie (PME). De onderstaande figuur toont een RAE-configuratie.

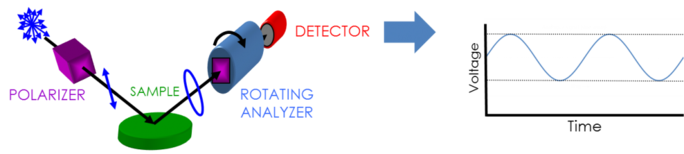
Gepolariseerd licht wordt door een lichtbron opgewekt en vervolgens door een polarisator gestuurd. De polarisator is zo ingesteld dat alleen licht met een bepaalde elektrische veldoriëntatie wordt doorgelaten. Aangezien de as van de polarisator is uitgelijnd tussen het p- en s-vlak, bereiken beide het oppervlak van het monster. Het nu lineair gepolariseerde licht wordt gereflecteerd door het oppervlak van het monster en wordt elliptisch gepolariseerd, waarna het door een continu roterende polarisator (de “analysator”) wordt gestuurd. De hoeveelheid licht die wordt doorgelaten hangt af van de oriëntatie van de polarisator ten opzichte van de elektrische veld ellips van het monster. Om de gereflecteerde polarisatie te bepalen, wordt het licht omgezet in een elektronisch signaal in de detector. Vergelijking van deze gegevens met de vastgestelde ingangspolarisatie levert informatie op over de verandering die door de reflectie van het monster wordt veroorzaakt: de ellipsometrische meting van Psi en Delta.

Gegevensanalyse

Ellipsometrie wordt gebruikt om de dikte van materiaalfolies of optische constanten te bepalen door de veranderingen in lichtpolarisatie te meten. “Pseudo” optische constanten uit de ellipsometermeting kunnen worden afgeleid door de gegevens die voor een enkele reflectie zijn bepaald, om te keren. Dit is nuttig voor bulkmateriaal.

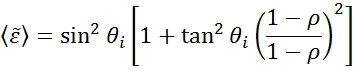
De bovenstaande vergelijking rekent niet met eventuele oppervlaktelagen. Niettemin is er normaal een oppervlakte-oxide of ruwheid in bulkmaterialen. Een directe inversie zal deze gegevens opnemen als deel van de optische bulkconstanten. Zie fig. 10 voor een overzicht van een typisch gegevensanalyseproces dat bij ellipsometriemetingen wordt gebruikt. Aangezien geen exacte vergelijking kan worden geschreven, is een regressieanalyse noodzakelijk. Het antwoord is vaak overgedetermineerd met slechts enkele onbekenden en honderden experimentele datapunten. Een regressieanalyse maakt het mogelijk alle gemeten gegevens mee te nemen bij het bepalen van de oplossing.

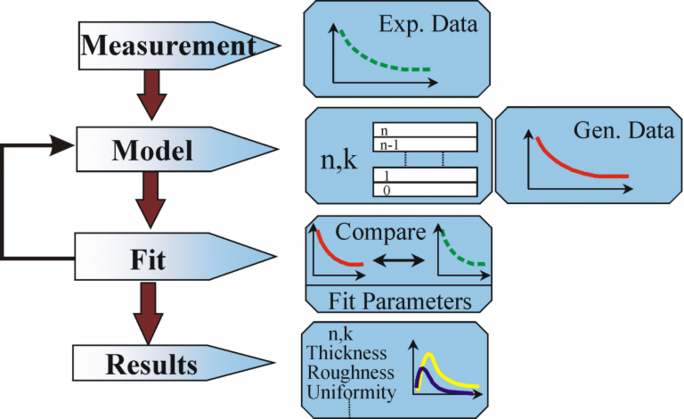
Figuur 10: Stroomschema voor ellipsometrie-gegevensanalyse.

De volgende procedure wordt gebruikt voor de gegevensanalyse: het monster wordt gemeten en er wordt een model van het monster gemaakt. Met behulp van dit model worden de veronderstelde resultaten van de vergelijkingen van Fresnel, die de dikte en de optische constanten van elk materiaal beschrijven, berekend. Indien deze waarden onbekend zijn, wordt een beoordeling van de voorlopige berekening gemaakt. De berekende waarden worden vergeleken met experimentele gegevens. Om de experimentele gegevens en de berekeningsgegevens beter op elkaar af te stemmen, kunnen onbekende materiaalgegevens worden gevarieerd. De experimentele gegevenspunten moeten echter altijd meer zijn dan de onbekende parameters. Zo kunnen bijvoorbeeld maximaal twee materiaaleigenschappen worden bepaald met een ellipsometer met één golflengte, aangezien deze precies twee gegevenspunten oplevert: Ψ, Δ (Psi en Delta). Regressie wordt gebruikt om de beste overeenkomst tussen model en experiment te vinden. Het verschil tussen de gegevenskrommen wordt gekwantificeerd met behulp van een schatter zoals de gemiddelde kwadraatfout (MSE). Onbekende eigenschappen worden gevarieerd tot de minimale MSE is bereikt. Dit betekent dat de laagste MSE gelijk is aan het beste antwoord.

Bekijk de onderstaande figuur voor de MSE-curve versus filmdikte voor een transparante film op silicium. De laagste MSE-waarde treedt op bij een dikte van 749 nm, ondanks een aantal lokale minima. De juiste filmdikte is dus ook 749 nm. Het regressiealgoritme zou een lokaal minimum als correct kunnen beschouwen. Om het juiste globale minimum te bepalen is het dus verstandig de resultaten op het oog te vergelijken voor de laagste MSE.

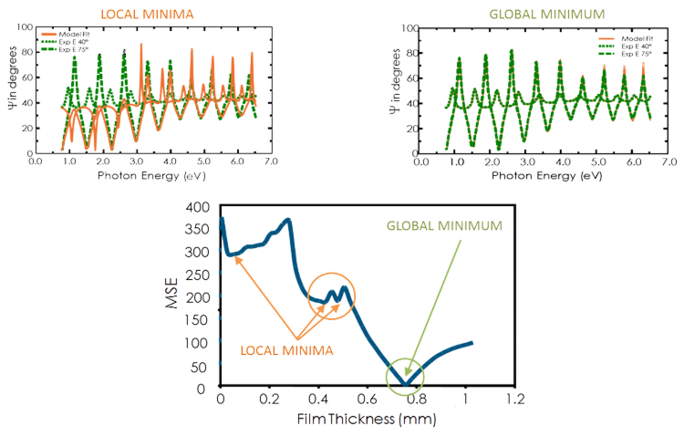
Figuur 11, rechtsboven: Experimentele gegevens en overeenkomstige curven gegenereerd voor het model op het globale minimum. Figuur 11, linksboven: Een soortgelijke kromme bij het lokale minimum in de buurt van een dikte van 0,45 µm kan gemakkelijk worden geïdentificeerd als een onjuist resultaat. Figuur 11, onder: De MSE-curve versus dikte toont het globale minimum. Een regressie-algoritme kan lokale minima geven, maar niet het eindresultaat.

Bepaling van de filmdikte

De filmdikte wordt gewoonlijk bepaald door de interferentie tussen licht dat van het oppervlak weerkaatst en het licht dat door de film reist. Of deze interferentie als constructief of destructief wordt beschouwd, hangt af van de relatieve fase van het licht dat samenvalt met de oppervlaktereflectie. De interferentie omvat zowel amplitude- als fase-informatie. De fase-informatie van Δ is zeer gevoelig voor films tot op submonolaagdikte. Zie de onderstaande figuur voor een vergelijking van de gereflecteerde intensiteit en de ellipsometrie voor dezelfde reeks dunne SiO2-lagen op Si. De reflectie voor elke film is bijna dezelfde terwijl er grote variaties in Δ.

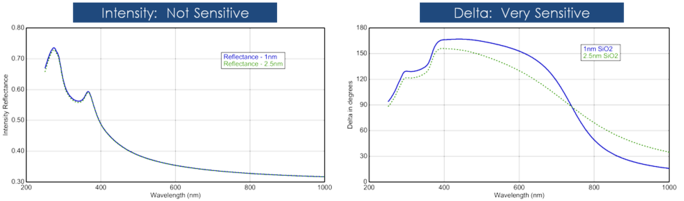
Figuur 12, links: Gereflecteerde intensiteit en ellipsometrische delta (rechts) voor twee dunne oxiden op silicium. Uit de intensiteitsmeting blijkt niet dat Delta zeer gevoelig is voor films van nanometerschaal.

Ellipsometrie wordt algemeen gebruikt voor films van sub-nanometers tot enkele microns dikte. Bij films dikker dan enkele tientallen microns kunnen interferentie-oscillaties slechts met toenemende moeite worden opgelost, behalve wanneer langere infrarode golflengten worden gebruikt. Daarom worden voor dikkere films gewoonlijk andere meettechnieken gebruikt.

Om de dikte te meten, moet een deel van het licht door de volledige film reizen en dan terugkeren naar het oppervlak. Bij licht-absorberende materialen kunnen optische diktemetingen alleen worden uitgevoerd op dunne en half-ondoorzichtige lagen, tenzij zij worden uitgevoerd op spectrale gebieden met minder absorptie. Bijvoorbeeld, een organische film die UV- en IR-licht absorbeert, kan doorzichtig zijn bij middellichtgolflengten. Metalen absorberen sterk bij alle golflengten, zodat de maximale laagdikte die kan worden bepaald rond 100 nm ligt.

Optische Constanten

Optische constanten spelen een belangrijke rol bij diktemetingen. De dikte van een film beïnvloedt de weglengte van het licht dat door de film reist, de index bepaalt de snelheid van de lichtgolf en de brekingshoek. Beide dragen dus bij tot de vertraging tussen het licht dat door de film reist en de oppervlaktereflectie. Het is noodzakelijk n en k, alsmede de dikte vast te stellen om correcte resultaten van een optische meting te verkrijgen.

Omdat de optische constanten van een materiaal voor verschillende golflengten variëren, moeten alle golflengten die met de ellipsometer worden geanalyseerd, afzonderlijk worden bepaald. De reactie van een materiaal bij elke golflengte kan worden voorspeld met behulp van een tabel met optische constanten. Om de moeizame aanpassing van onbekende optische constanten golflengte-voor-golflengte te vermijden, is het gunstig om alle golflengten tegelijk te gebruiken. De instelbare parameters van een dispersierelatie bijvoorbeeld maken het mogelijk de vorm van de totale optische constante aan te passen aan de experimentele resultaten. In vergelijking met het instellen van afzonderlijke n- en k-waarden voor elke golflengte, wordt het aantal onbekende vrije parameters aanzienlijk verminderd.

Cauchy- of Sellmeier-relaties worden vaak gebruikt om de index voor transparante materialen te beschrijven, waarbij de Cauchy-relatie gewoonlijk wordt gegeven als:

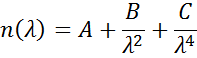
met de drie termen die passen bij de brekingsindex voor het materiaal. De Cauchy-relatie is niet beperkt door de Kramers-Kronig (KK) consistentie en kan leiden tot onfysische dispersie. De Sellmeier-relatie daarentegen legt Kramers-Kronig (KK)-consistentie op, die ervoor zorgt dat de optische dispersie een realistische vorm behoudt. De Sellmeier-relatie wordt meestal geschreven als:

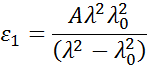
Absorberende materialen hebben vaak een transparant golflengtegebied dat met de Cauchy- of Sellmeier-relatie kan worden gemodelleerd. Terwijl het absorberende gebied echter rekening moet houden met zowel reële als imaginaire optische constanten. Om de absorptie voor verschillende materialen te beschrijven, wordt in veel dispersierelaties gebruik gemaakt van de oscillatortheorie, waaronder Lorentz, Harmonic, en Gauss. Zij hebben alle dezelfde eigenschappen, waarbij de absorptie-eigenschappen worden beschreven met amplitude, verbreding en middelpuntsenergie (gerelateerd aan de frequentie van het licht). De vorm van de reële component wordt berekend met behulp van Kramers-Kronig consistentie nadat het imaginaire gedrag door de oscillator is beschreven. Om eventuele extra absorptie buiten het gemeten spectrale gebied op te nemen wordt een offset aan de reële component toegevoegd. De Lorentz-oscillator kan worden geschreven als:

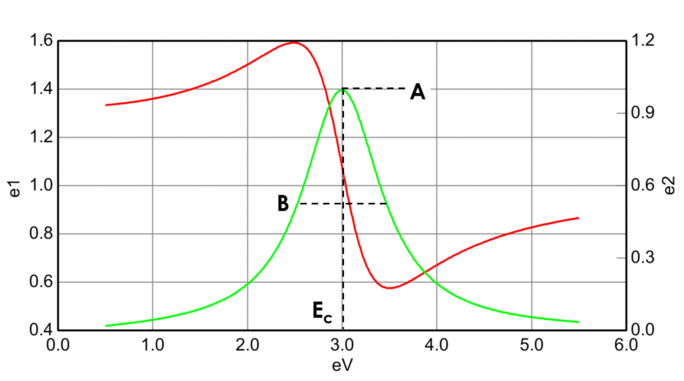
Figuur 13 toont ook Amplitude (A), Verbreding (B), Centrerenergie (Ec) en offset (e1, off set) voor een typische Lorentz-oscillator. De energie E is gerelateerd aan de frequentie van een golf, n:

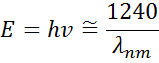
De constante van Planck h en de golflengte λ zijn gegeven in nanometers. Andere dispersiemodellen, zoals Tauc-Lorentz en Cody-Lorentz, bevatten termen om de bandkloofenergie te beschrijven.

Verder lezen

Ellipsometrie is een gevestigde optische techniek voor het meten van dunne films en bulkmaterialen. Het maakt gebruik van de polarisatieveranderingen veroorzaakt door reflectie/transmissie van een materiaalstructuur om de eigenschappen van het materiaal te bepalen, zoals dikte en optische constanten.

Aspnes D.E. (1985). De nauwkeurige bepaling van optische eigenschappen door Ellipsometrie. In: Palik E.D. (ed.) Handbook of Optical Constants of Solids, pp. 89-112. Academic Press, Orlando.

Azzam R.M.A. and Bashara N.M. (1987). Ellipsometry and Polarized Light, Elsevier Science B.V., Amsterdam, The Netherlands.

Boccara A.C., Pickering C., and Rivory J. (eds.), (1993). Spectroscopic Ellipsometry, Elsevier Publishing, Amsterdam.

Collins R.W., Aspnes D.E., and Irene E.A. (eds.), (1998). “Proceedings from the Second International Conference on Spectroscopic ellipsometry”. In: Thin Solid Films, vols. 313-314.

Fujiwara H., Spectroscopic Ellipsometry, Principles and Applications, John Wiley & Sons, Ltd. 2007

Gottesfeld S., Kim Y.T., and Redondo A. (1995). “Recente toepassingen van ellipsometrie en spectroellipsometrie in elektrochemische systemen”, In: I. Rubinstein (ed.), Physical Electrochemistry: Principles, Methods, and Applications, Marcel Dekker, New York.

Herman, I.P. (1996). Optical Diagnostics for Thin Film Processing, pp 425-479. Academic Press, San Diego, California.

Johs B. et al (1999). “Overview of Variable Angle Spectroscopic Ellipsometry (VASE), Part II: Advanced Applications”. Optische Metrologie, vol. CR72, pp 29-58. SPIE, Bellingham, Washington.

Johs B. et al (2001). “Recent Developments in Spectroscopic Ellipsometry for in situ Applications”. In: Duparré A, Singh B (ed.) Optical Metrology Roadmap for the Semiconductor, Optical, and Data Storage Industries II, vol. 4449, pp 41-57. SPIE, Bellingham, Washington.

Roseler A. (1990). Infrared Spectroscopic Ellipsometry, Akademie-Verlag, Berlin.

Rossow U. and Richter W. (1996). “Spectroscopische Ellipsometrie” in: Bauer G and Richter W (eds.) Optical Characterization of Epitaxial Semiconductor Layers, pp. 68-128, Springer-Verlag, Berlin.

Tompkins H.G. (1993). A User’s Guide to Ellipsometry, Academic Press, San Diego, California.

Tompkins H.G. and McGahan W.A. (1999). Spectroscopic Ellipsometry and Reflectometry, John Wiley & Sons, Inc., USA.

Tompkins, H.G. and Irene E.A. (eds.), 2005, Handbook of Ellipsometry, William Andrew Publishing, New York.

Tompkins, H. G. and Hilfiker, J. H., Spectroscopic Ellipsometry, Practical Application to Thin Film Characterization, 2016, Momentum Press Engineering

Woollam J.A. and Snyder P.G. (1992). “Variable Angle Spectroscopic Ellipsometry” in: Brundle CR, Evans CA, and Wilson S (eds) Encyclopedia of Materials Characterization: Surfaces, Interfaces, Thin Films, pp. 401-411, Butterworth-Heinemann, Boston.

Woollam J.A. et al (1999). “Overview of Variable Angle Spectroscopic Ellipsometry (VASE), Part I: Basic Theory and Typical Applications”. Optische Metrologie, vol. CR72, pp 3-28. SPIE, Bellingham, Washington.

Woollam J.A. (2000). “Ellipsometry, Variable Angle Spectroscopic” in: Webster J.G. (ed.) Wiley Encyclopedia of Electrical and Electronics Engineering, pp. 109-116. John Wiley & Sons, New York.