door Marco Taboga, PhD
De indicatorfunctie van een gebeurtenis is een willekeurige variabele die de waarde 1 krijgt als de gebeurtenis plaatsvindt en de waarde 0 als de gebeurtenis niet plaatsvindt. Indicatorfuncties worden in de kansrekening vaak gebruikt om de notatie te vereenvoudigen en stellingen te bewijzen.
Definitie
Hier volgt een formele definitie.
Definitie Stel 
is een steekproefruimte en is een gebeurtenis. De indicatorfunctie (of indicator random variable) van de gebeurtenis , aangeduid met , is een random variabele die als volgt is gedefinieerd: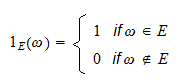
Terwijl de indicator van een gebeurtenis gewoonlijk wordt aangeduid met , wordt hij soms ook aangeduid met waarbij de Griekse letter Chi is.
Voorbeeld We gooien met een dobbelsteen en een van de zes getallen van 1 tot en met 6 kan met de beeldzijde naar boven verschijnen. De voorbeeldruimte isBepaal de gebeurtenis beschreven door de zin “Een even getal verschijnt open”. Een willekeurige variabele die de waarde 1 krijgt wanneer een even getal open verschijnt en anders de waarde 0, is een indicator van de gebeurtenis . De casusgewijze definitie van deze indicator is
Uit bovenstaande definitie kan gemakkelijk worden opgemaakt dat een discrete willekeurige variabele is met steun en kansmassafunctie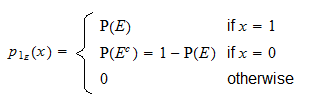
Eigenschappen
Indicatorfuncties hebben de volgende eigenschappen.
Machten
De -de macht van is gelijk aan :want kan zowel als zijn en
Verwachte waarde
De verwachte waarde van is gelijk aan :
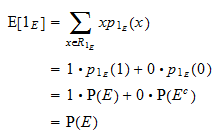
Variantie
De variantie van is gelijk aan . Dankzij de gebruikelijke variantieformule en de machteneigenschap hierboven, verkrijgen we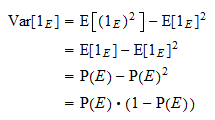
Intersecties
Als en twee gebeurtenissen zijn, danwant:
-
als
, dan en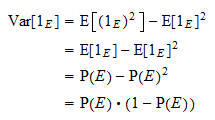
-
als
, danen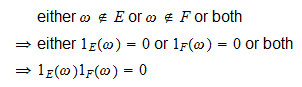
Indicatoren van nul-probabiliteitgebeurtenissen
Stel is een nul-probabiliteitgebeurtenis en een integreerbare willekeurige variabele. Dan Hoewel een rigoureus bewijs van dit feit buiten het bestek van deze inleidende uiteenzetting valt, zou deze eigenschap intuïtief moeten zijn. De willekeurige variabele is gelijk aan nul voor alle monsterpunten behalve eventueel voor de punten . De verwachte waarde is een gewogen gemiddelde van de waarden die kan aannemen, waarbij elke waarde wordt gewogen met zijn respectieve waarschijnlijkheid. De waarden die niet nul kunnen aannemen, worden gewogen met kansen nul, dus moet nul zijn.
Oplossingen
Hieronder vindt u enkele oefeningen met verklaarde oplossingen.
Oefening 1
Beschouw een willekeurige variabele en een andere willekeurige variabele gedefinieerd als een functie van .
Druk uit met behulp van de indicatorfuncties van de gebeurtenissen en .
Noem met de indicator van de gebeurtenis en geef met de indicator van de gebeurtenis . We kunnen schrijven als
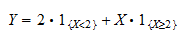
Oefening 2
Laat een positieve willekeurige variabele zijn, dat wil zeggen een willekeurige variabele die alleen positieve waarden kan aannemen. Zij een constante. Bewijs dat waar de indicator is van de gebeurtenis .
Merk eerst op dat de som van de indicatoren en altijd gelijk is aan :Dientengevolge kunnen we schrijven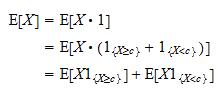
Nou, merk op dat een positieve willekeurige variabele is en dat de verwachte waarde van een positieve willekeurige variabele positief is:Dus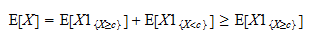 
Oefening 3
Laat een gebeurtenis zijn en geef de indicatorfunctie ervan weer door . Zij het complement van en geef de indicatorfunctie ervan weer met . Kunt u uitdrukken als een functie van ?
De som van de twee indicatoren is altijd gelijk aan :Daarom,
Hoe citeren
Gelieve te citeren als:
Taboga, Marco (2017). “Indicatorfuncties”, Hoorcolleges over kansrekening en mathematische statistiek, Derde druk. Kindle Direct Publishing. Online bijlage. https://www.statlect.com/fundamentals-of-probability/indicator-functions.