Het Ising-model is een bijzonder voorbeeld van een thermodynamisch systeem, en het is het modelsysteem voor het begrijpen van fase-overgangen. Weet je dat biologen zoveel tijd besteden aan fruitvliegjes? Natuurkundigen besteden veel tijd aan het Ising model. Zoals Prof. Raghu ons behulpzaam vertelt, is het de Drosophila van de faseovergangen.

Persoonlijk ben ik niet zo’n fan van zijn analogie, omdat ik fruitvliegjes smerig vind. Hopelijk is het Ising-model niet te smerig.

Motivatie

Waarom besteden we zoveel tijd aan het Ising-model?

• Het is verrassend nuttig om ons te helpen nadenken over allerlei gedragingen die met fase-overgangen te maken hebben. Bijvoorbeeld:

  • het Ising-model vertoont symmetriebreking in lage-temperatuurfase (waar we het zojuist over hebben gehad)

  • het heeft een speciaal ‘kritisch punt’ bij een welbepaalde temperatuur (waar we in het fasediagram van water op zinspeelden)

  • andere rijke eigenschappen.

• Het is een van de weinige exact oplosbare modellen waarmee we daadwerkelijk thermodynamische grootheden kunnen berekenen en interpreteren.

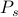  • In het algemeen is het berekenen van thermodynamische grootheden moeilijk omdat je veel termen moet optellen. Herinner u uit onze eerste thermo-les dat u een evenwichtssysteem kunt beschouwen als een ensemble van vele toestanden , elk gewogen met hun eigen waarschijnlijkheid . In dit kader komen de thermodynamische grootheden die je waarneemt overeen met gemiddelden over het ensemble. In het bijzonder, als u het ensemblegemiddelde van een of andere waarneembare 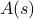wilt vinden, moet u de som 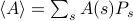vinden, waarbij de som over alle mogelijke toestanden loopt. Het probleem hierbij is, zoals u zich herinnert, dat het aantal toestanden van een thermodynamisch systeem exponentieel toeneemt met het aantal deeltjes! Zelfs voor een systeem van gemiddelde grootte zijn er gewoon te veel toestanden voor een computer om het gemiddelde expliciet te berekenen – laat staan voor een thermodynamisch systeem met 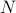in de orde van .

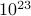  • We moeten dus ”slim” zijn om de partitiefunctie te berekenen, en we moeten dankbaar zijn voor exact oplosbare systemen!

• Het Ising-model is eenvoudig, maar kan worden toegepast op een verrassend aantal verschillende systemen.

  • Dit is onze eerste kennismaking met universaliteit – een kenmerk van kritische verschijnselen waarbij dezelfde theorie van toepassing is op allerlei verschillende faseovergangen, of het nu gaat om vloeistoffen en gassen of magneten of supergeleiders of wat dan ook. Natuurkundigen zijn dol op dit soort algemeen gedrag, omdat het een soort diepere orde in onze chaotische wereld suggereert.

Definitie van het Ising-model

Het Ising-model is een wiskundig model dat niet overeenkomt met een echt fysisch systeem. Het is een enorm (vierkant) raster van sites, waarbij elke site in één van twee toestanden kan zijn. We labelen elke site met een index , en we noemen de twee toestanden en . Om te zeggen dat de ‘e site in de toestand is, schrijven we .

Nou, deze definitie is jammerlijk abstract en onfysisch, dus voor ons natuurkundigen is het uiterst nuttig om een echt systeem in gedachten te hebben, zodat we kunnen verwijzen naar iets expliciet en een fysische intuïtie kunnen opbouwen. Hier volgen een paar fysische systemen die het Ising-model zou kunnen voorstellen:

• Een magneet. Elke plaats vertegenwoordigt een bepaalde “spin” in het materiaal (een ongepaard elektron??), en het is als de spin naar beneden wijst of als de spin naar boven wijst. Elk van de spins gedraagt zich als een mini-magneetje met een eigen mini-magnetisch moment; als alle spins op één lijn staan, gedraagt het hele rooster van spins zich als een grote magneet met een netto macroscopisch magnetisch moment.

• Een legering; zeg maar messing. Elk van de plaatsen is een atoom in het rooster; staat voor een koperatoom op die plaats; staat voor zink.

• Een ”rooster gas”. Elk van de plaatsen is de mogelijke plaats van een deeltje; betekent dat de plaats leeg is en betekent dat de plaats bezet is door een deeltje.

• Bacteriële vortex-roosters??

Voorlopig zullen we het Ising-model zien als een model voor een magneet. Het is zeker een sterk vereenvoudigd speelgoedmodel van een magneet, maar de magneet-analogie kan niettemin onze gekoesterde natuurkundige intuïtie helpen sturen.

De Hamiltoniaan samenstellen

Een natuurlijke vraag om over dit Mickey-muis-model van een magneet te stellen, is welke energie het heeft. Om precies te zijn, we willen een functie opschrijven die de energie weergeeft van elke mogelijke configuratie (ook wel microtoestand genoemd) van de spins in de magneet. Zoals bekend wordt deze energiefunctie de Hamiltoniaan genoemd.

In het Ising-model omvat de Hamiltoniaan twee soorten interacties:

• de externe veldterm. Zoals we ons uit de kwantummechanica herinneren, kan een extern magnetisch veld de energieën van de spin-down- en spin-up-toestand splitsen, zodat de ene hoger in energie is en de andere lager.

  • De grootte van geeft aan hoe sterk het veld is, dus hoeveel hoger de ene spin in energie is dan de andere.

  • Het teken van geeft aan of de voorkeur uitgaat naar spin-up of spin-down.

  • Omdat elke individuele spin het externe veld voelt, moeten we alle sites bij elkaar optellen om de totale bijdrage aan de energie te vinden.

• de interactieterm tussen naburige spins – misschien willen ze met elkaar uitlijnen en dezelfde kant op wijzen, misschien willen ze uitlijnen en op verschillende manieren wijzen. Natuurkundig kunnen we ons voorstellen dat deze interactie ontstaat omdat elke spin in de magneet zijn eigen mini magnetische dipool is die zijn eigen magnetisch veld opwekt, en zijn buren kunnen dat magnetisch veld voelen.

  • De grootte van vertelt je hoe sterk naburige spins aan elkaar gekoppeld zijn – hoe graag ze willen (anti-)uitlijnen. Natuurkundig gezien zou de sterkte van de spin-spin-koppeling bijvoorbeeld kunnen afhangen van de afstand tussen de spins in het magneetrooster.

  • Het teken van vertelt je of de buren de voorkeur geven aan uitlijnen of aan anti-uitlijnen. (De technische term hiervoor is respectievelijk ferromagnetisch of anti-ferromagnetisch). Of een materiaal het ene of het andere is (of geen van beide), hangt af van de precieze kwantummechanische details van de wisselwerking tussen de spins.

  • Aangezien de spin-spin wisselwerking ontstaat tussen twee spins, moeten we de som maken over paren van plaatsen om de totale wisselwerking met de energie te vinden.

Meer over de interactieterm

Een natuurlijke vraag over de spin-spin interactieterm is welke spins zijn gekoppeld aan welke spins?

Als we weer teruggaan naar het fysische beeld van de magneet, en we zoomen in op een bepaalde spin, dan zouden we verwachten dat de sterkte van de spin-spin interactie sterker is voor nabije spins en zwakker voor verafgelegen spins. De exacte afstandsafhankelijkheid van spin-spin interacties is waarschijnlijk nogal gecompliceerd voor echte magneten.

Voor het Ising model maken we de eenvoudigst mogelijke aanname voor de aard van deze spin-spin interactie:

Een paar opmerkingen:

• In een vierkant rooster van dimensies heeft elke plaats 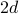naaste buren: links en rechts in één dimensie, boven en onder als je de tweede dimensie toevoegt, enz…

• We nemen aan dat de interactie isotroop is – alle buren worden gelijk behandeld, ongeacht de richting.

• Wij spreken vaak over naaste-buurtinteracties als de energie van een binding die twee roosters met elkaar verbindt.

• Wanneer we aangrenzende paren van plaatsen bij elkaar optellen, schrijven we symbolisch kleine haakjes rond de indices om ”naaste buur” aan te geven.

Een leuk gevolg van de naaste-buurtinteracties is dat we, wanneer we de totale energie van een bepaalde configuratie van spins zoeken, in plaats van alle mogelijke paren van plaatsen bij elkaar op te tellen, alleen paren van plaatsen bij elkaar optellen die aan elkaar grenzen.

Nu we al deze dingen hebben besproken, zijn we klaar om de eigenlijke uitdrukking voor de Hamiltoniaan op te schrijven. (Ik wilde eerst de natuurkunde uitleggen en interpreteren voordat ik de Hamiltoniaan opschreef, zodat de symbolen enigszins zinvol waren.)

Hamiltoniaan van het Ising Model

De Hamiltoniaan van het Ising Model kan worden geschreven als

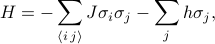
waar de spin-spin wisselwerking weergeeft, het externe veld voorstelt, en de 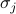de individuele spins zijn op elk van de roosterplaatsen. De eerste som is over alle paren van naburige roosterplaatsen (ook wel bindingen genoemd); deze som vertegenwoordigt de interacties tussen de spins. De tweede som is over alle roosterplaatsen zelf; zij stelt het externe veld voor dat probeert alle spins in één richting te brengen.

Ga verder met de thermodynamica van het Ising model.