Wat is de helling-afsnijvorm

Helling-afsnijvorm is een van de drie vormen die we kunnen gebruiken om een rechte lijn uit te drukken. De andere vormen zijn de punt-hellingvorm en de standaardvorm, maar in dit deel zullen we vooral de helling-afsnijvorm gebruiken. Met de helling-aftekenvorm drukken we de vergelijking van een rechte uit als:

y=mx+by = mx + by=mx+b

Je weet misschien dat xxx en yyy coördinaten van een punt op een grafiek zijn, maar wat zijn mmm en bbb?

Wat is b in y=mx+b?

De letter b is een getal dat aangeeft wanneer de rechte de y-as raakt. We noemen dit ook wel het “y-afsnijpunt”. Laten we bijvoorbeeld een rechte lijn tekenen op het assenvlak.

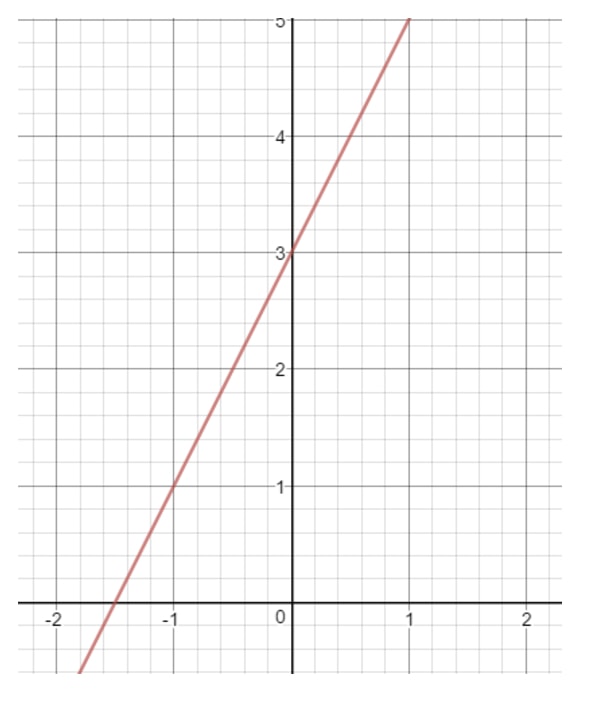
Als je goed naar de y-as zou kijken, raakt de rechte lijn de y-as op een specifieke plaats. Waar is die plaats? Dat is het getal 3, want daar snijden de y-as en de lijn elkaar. Dit betekent dat we kunnen concluderen dat b = 3.

Wat is m in de vorm van helling-afteken?

De letter m is een getal dat de helling van de lijn weergeeft. Sommigen noemen de helling de toename ten opzichte van de afname. Als we twee punten hebben, dan kunnen we de richtingscoëfficiënt van die twee punten vinden met behulp van de hellingsformule

m=riserun=y2-y1x2-x1m = \frac{stijging}{oploop} = \frac{y_{2} – y_{1}}{x_{2} – x_{1}}m=runrise=x2-x1y2-y1

Hetzelfde idee werkt hier. Als we twee willekeurige punten op een rechte lijn nemen, dan kunnen we de helling van de lijn vinden met de bovenstaande formule! Laten we bijvoorbeeld deze lijn gebruiken.

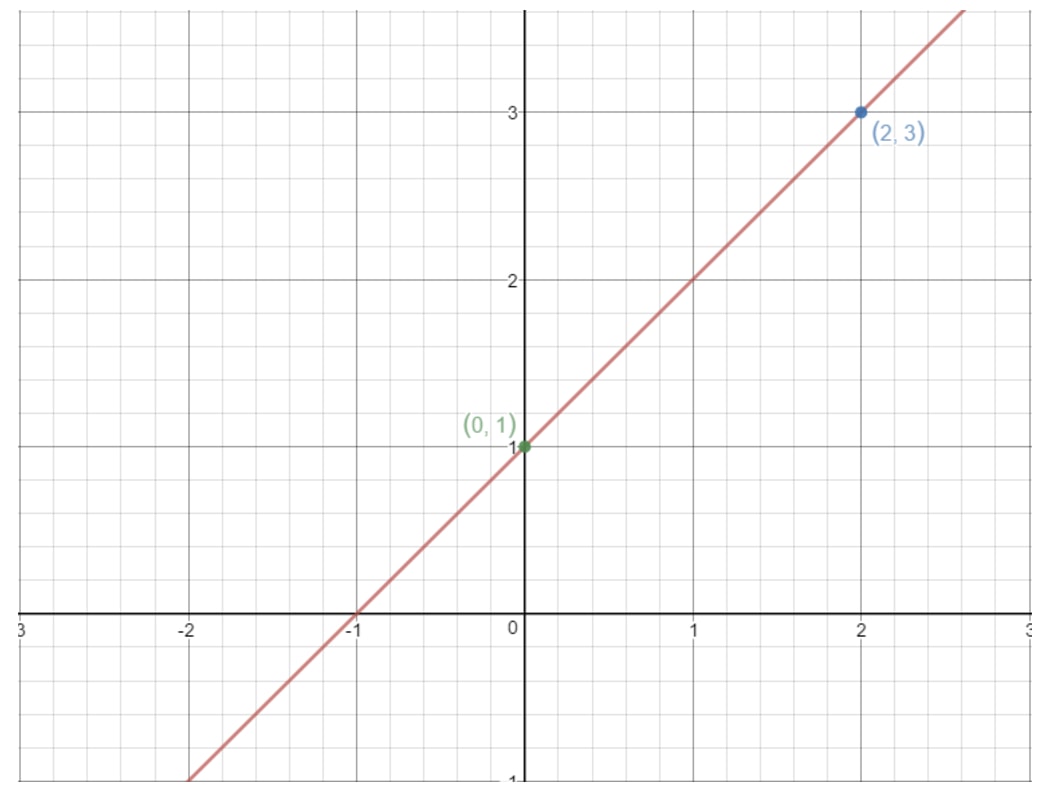
Merk op dat de punten (2, 3) en (0, 1) op deze grafiek liggen. Waarom gebruiken we deze twee punten dan niet om de helling van de lijn te vinden? Met de formule zouden we krijgen:

m=y2-y1x2-x1=1-30-2m = \frac{y_{2} – y_{1}}{x_{2} – x_{1}} = \frac{1 – 3}{0 – 2}m=x2-x1y2-y1=0-21-3=-2-2= \frac{-2}{-2}=-2-2=1= 1=1

Dat betekent dat de helling van deze lijn 111 is!

Het bijzondere van hellingen is dat we elke twee punten op de lijn kunnen gebruiken om de helling te vinden. Dus als je twee verschillende punten op deze lijn zou nemen, zou je nog steeds krijgen dat de helling 111 is.

Hoe schrijf je een vergelijking in helling-aftekenvorm?

Je weet misschien hoe de helling-aftekenvorm eruitziet, maar de helft van de tijd krijg je vergelijkingen die niet in die vorm zijn. Dus is het jouw taak om ze om te zetten in een schuine-afsnijvorm. Hoe doen we dat? Het doel is om altijd de yyy term te isoleren. Bijvoorbeeld, je krijgt de vergelijking

6x+4+2y=06x + 4 + 2y = 06x+4+2y=0

Om yyy te isoleren, verplaatsen we 6x+46x + 46x+4 naar de rechterkant van de vergelijking

2y=-6x-42y = -6x – 42y=-6x-4

Nu zit de 222 in de weg van yyy, dus die gaan we wegwerken door beide kanten van de vergelijking door 222 te delen.

2y2=-6x-42\frac{2y}{2} = \frac{-6x – 4}{2}22y=2-6x-4y=-6×2-42y = -\frac{6x}{2} – \frac{4}{2}y=-26x-24y=-3x-2y = -3x – 2y=-3x-2

Omdat yyy geïsoleerd is, kan je zien dat het in de helling-intercept vorm y=mx+by = mx + by=mx+b waar m=-3m = -3m=-3, en b=-2b = -2b=-2 is.

Nu we het y-afsnijpunt en de helling heel goed kennen, kunnen we specifieke vragen over het vinden van die vormen gaan beantwoorden!

Hoe vind je de y-afsnijlijn?

Vraag 1: Gebruik de lineaire vergelijking y=12x+5y = \frac{1}{2} x + 5y=21x+5, vind de y-afsnijlijn.

Merk op dat de vergelijking al in de helling-afsnijvorm y=mx+by = mx + by=mx+b is. We hoeven alleen maar uit te vinden wat bbb is. We zien dat b=5b = 5b=5, dus het y-afsnijpunt is 555.

Laten we een iets moeilijkere vraag doen.

Vraag 2: Bepaal het y-afsnijpunt van 2x-4y=82x – 4y = 82x-4y=8

Nu is deze lineaire vergelijking niet in de helling-afsnijvorm, dus moeten we hem eerst in die vorm veranderen. Ons doel is om yyy in deze vergelijking te isoleren.

Zien we dat als we de 2x2x2x naar de rechterkant van de vergelijking verplaatsen, we krijgen:

-4y=8-2x-4y = 8 – 2x-4y=8-2x

Delen we nu beide zijden door -4-4-4, dan krijgen we:

-4y-4=8-2x-4}= \frac{-4y}{-4} = \frac{8 – 2x}{-4}-4-4y=-48-2xy=8-4-2x-4y = \frac{8}{-4} – \frac{2x}{-4}y=-48–42xy=-2+12xy = -2 + \frac{1}{2}xy=-2+21x

Nu de posities van de twee termen verwisselen geeft ons:

y=12x-2y = \frac{1}{2}x – 2y=21x-2

Vraag 3: Bepaal het y-afsnijpunt van 4y-8=04y – 8 = 04y-8=0.

Dit ziet er misschien een beetje vreemd uit omdat er geen xxx term is, maar ons doel blijft hetzelfde. We gaan yyy isoleren.

Door de -8-8-8 naar de rechterkant van de vergelijking te verplaatsen, krijgen we:

4y=84y = 84y=8

Deel beide zijden van de vergelijking door 444 geeft ons

4y4=84\frac{4y}{4} = \frac{8}{4}44y=48y=2y = 2y=2

Nu ziet dit er misschien niet zo uit, maar de vergelijking is in helling-aftapvorm. Het is gewoon dat m=0m = 0m=0, dus de hele mxmxmx term is verdwenen. Herschrijf de vergelijking gewoon als

y=0m+2y = 0m + 2y=0m+2

Uit het observeren kunt u afleiden dat b=2b = 2b=2, en dus is het y-afsnijpunt 222. Laten we nog een vraag doen.

Vraag 4: Bepaal (indien mogelijk) het y-afsnijpunt van 5x-15=05x – 15 = 05x-15=0.

Deze is interessant omdat de vergelijking geen yy-term heeft. Hoe moeten we die dan in de vorm van een hellend intercept gieten? Nou, het enige wat we nu kunnen doen is isoleren voor xxx, dus laten we dat nu proberen.

Verplaats de 151515 naar het rechterlid van de vergelijking en je hebt:

5x=155x = 155x=15

Deling van beide zijden van de vergelijking geeft:

5×5=155x{5} = \frac{15}{5}55x=515x=3x = 3x=3

Nu gaan we dit in een grafiek tekenen. Merk op dat in deze vergelijking, xxx gedwongen wordt 333 te zijn en niets anders kan zijn. Er staat echter niets over yyy, dus yyy kan alles zijn wat het wil. Als we een waardetabel schrijven, krijgen we:

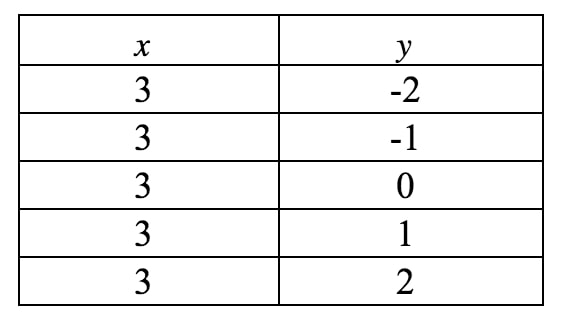
Als we deze punten uitzetten op een assenvlak en de lijn trekken, krijgen we:

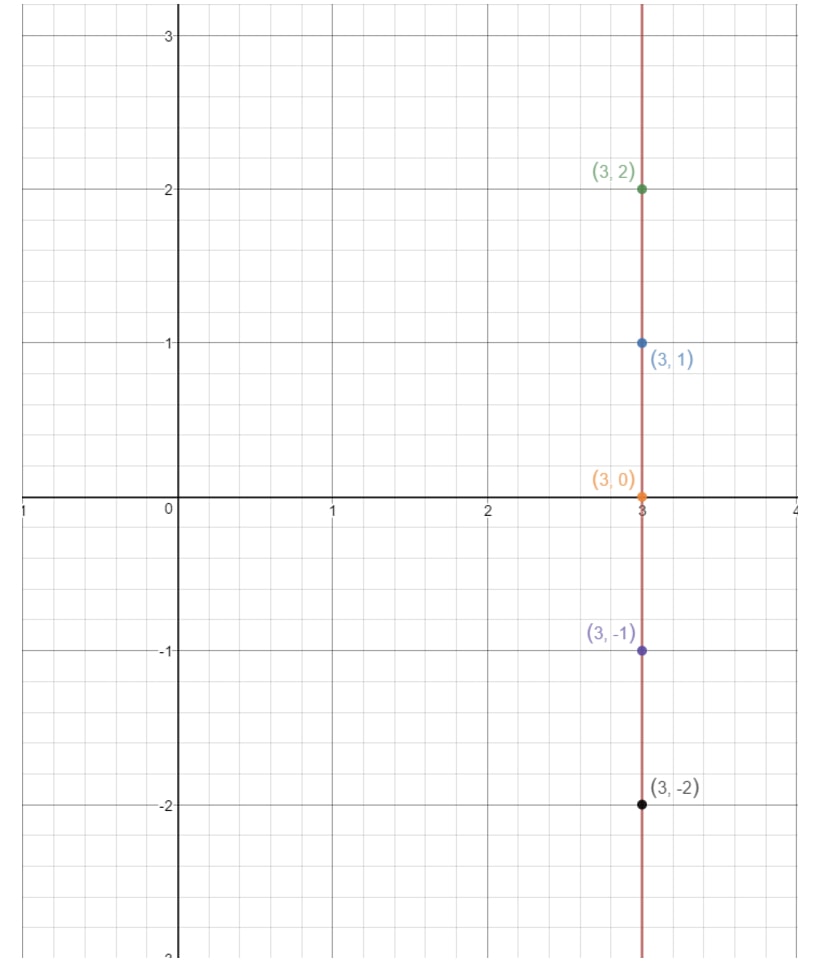
Merk op hoe de lijn nooit de y-as raakt. Dit betekent dat de vergelijking geen y-afsnijpunt heeft. Nu we alle gevallen van het vinden van het y-afsnijpunt hebben behandeld, gaan we kijken naar vragen die ons vragen om de helling te vinden!

Hoe vind je de helling van een vergelijking?

Vraag 5: Bepaal de helling van y=32x+1y = \frac{3}{2}x + 1y=23x+1

Vraag 6: Bepaal de helling van de lineaire vergelijking 6x-6y=06x – 6y = 06x-6y=0

Zoals je ziet is de vergelijking niet in de helling-afteken vorm, dus moeten we haar eerst in die vorm omzetten. Ons doel is om yyy te isoleren.

Het verplaatsen van 6x6x6x naar de rechterkant van de vergelijking geeft:

-6y=-6x-6y = -6x-6y=-6x

Het delen van beide zijden door -6-6 geeft:

-6y-6=-6x-6frac{-6y}{-6} = \frac{-6x}{-6}-6-6y=-6-6xy=xy = xy=x

Merk op dat dit eigenlijk in helling intercept vorm is y=mx+by = mx + by=mx+b. Alleen is het y-afsnijpunt bbb in dit geval 000, en xxx is hetzelfde als 1x1x1x. We kunnen de vergelijking dus herschrijven tot:

y=1x+0y = 1x + 0y=1x+0

Nu door te observeren, zien we dat m=1m = 1m=1. Aangezien mmm de helling is, dan moet de helling 111 zijn. Laten we een iets moeilijkere doen

Vraag 7: Bepaal de helling van 2y-4=02y – 4 = 02y-4=0

Ook dit is een beetje vreemd omdat we geen xxx term hebben. Ons doel om yyy te isoleren blijft echter hetzelfde.

Verplaats -4-4-4 naar de rechterkant van de vergelijking en we hebben:

2y=42y = 42y=4

Deling van beide kanten van de vergelijking door 222 geeft:

2y2=42\frac{2y}{2} = \frac{4}{2}22y=24y=2y = 2y=2

Zie hier dat het nu in helling-aftapvorm is, behalve dat de term mxmxmx verborgen is omdat m=0m = 0m=0. We kunnen onze vergelijking dus herschrijven als:

y=0x+2y = 0x + 2y=0x+2

Omdat m=0m = 0m=0, hebben we dus een nul-helling. Als je je afvraagt hoe een lijn met 000 helling eruit ziet, dan is hier een grafiek om te zien.

Vraag 8: Vind (indien mogelijk) de helling van de lineaire vergelijking 16-4x=016 – 4x = 016-4x=0

In dit geval kan yyy niet geïsoleerd worden omdat er geen yyy term is. Dus het enige wat we kunnen doen is xxx isoleren.

Verplaatsing van 161616 naar de rechterkant van de vergelijking geeft:

-4x=-16-4x = -16-4x=-16

Deelt men beide zijden door -4-4-4, dan krijgt men:

-4x-4=-16-4frac{-4x}{-4} = \frac{-16}{-4}-4-4x=-4-16x=4x = 4x=4

Dit is nog steeds niet in helling-aftekenvorm, dus onze enige hoop om de helling te verkrijgen is een grafiek van deze lijn te tekenen. Ook hier zien we dat xxx altijd gedwongen wordt 444 te zijn, maar yyy kan alles zijn wat het wil omdat er geen yyy term is. Als we een waardetabel zouden schrijven, krijgen we:

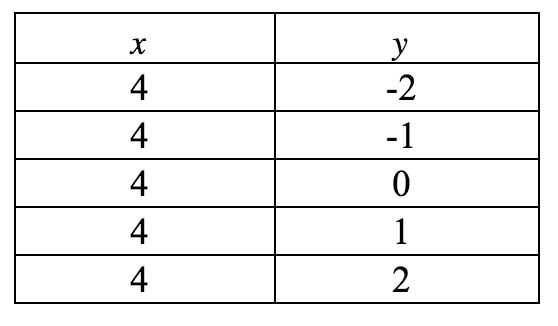
Als we deze punten op een assenvlak uitzetten en de lijn tekenen, krijgen we:

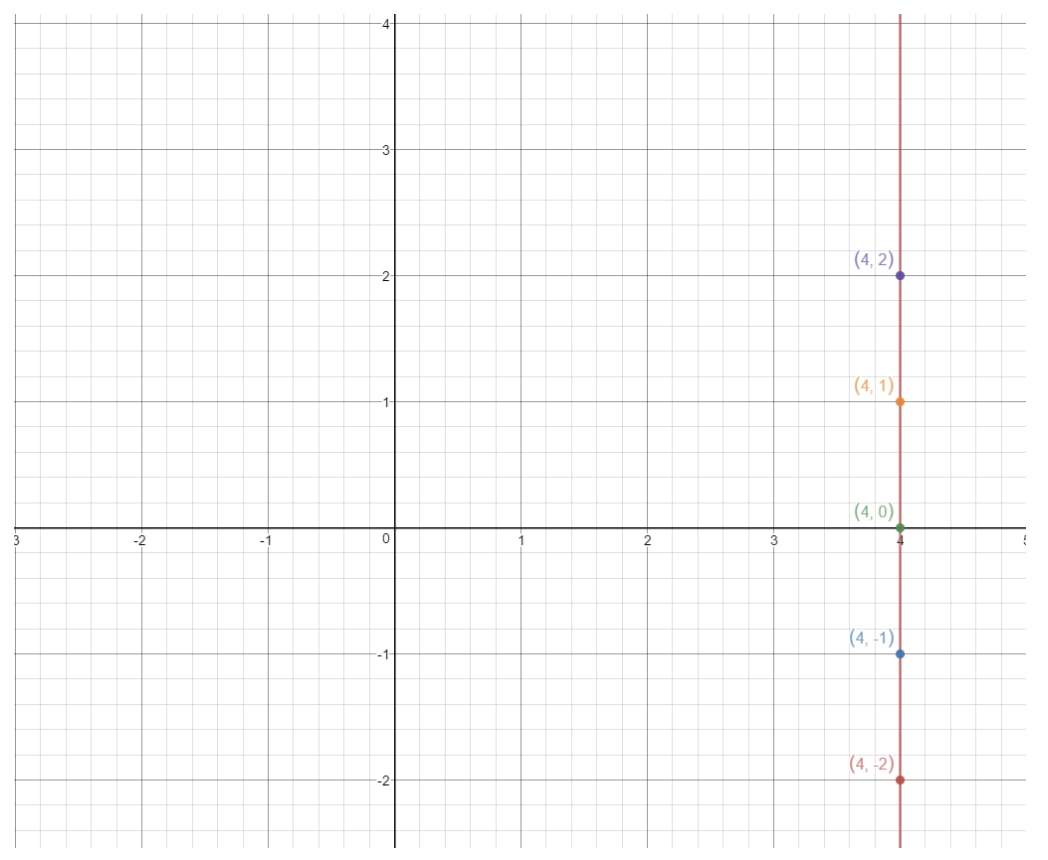
Dit is een verticale lijn. Dus wat is de helling van een verticale lijn? Laten we dat proberen uit te zoeken door de stijging en de daling te vinden. Zie hoe deze lijn altijd oneindig stijgt, maar er is geen enkele aanloop. Dus dat betekent dat het verloop 000 is. Dus als we de helling berekenen, dan krijgen we:

m=stijging=opgang0=onbepaaldm = \frac{opgang}{opgang} = \frac{opgang}{0} = onbepaaldm=opgang=0opgang=onbepaald

We kunnen niet delen door 000, dus we hebben eigenlijk een onbepaalde helling.

Wat is een ongedefinieerde helling?

Een ongedefinieerde helling is een helling die in de grafiek recht omhoog gaat. Zoals in de grafiek hierboven te zien is, stijgt de helling oneindig en heeft geen verloop. We krijgen dus een ongedefinieerde helling omdat we niet kunnen delen door 000.

In het algemeen krijgen we altijd een ongedefinieerde helling als we een rechte verticale lijn krijgen!

Laten we eens kijken naar enkele andere unieke vragen!

Vergelijking vinden uit één punt

Vraag 9: Een punt (2, 6) gaat door een vergelijking van y=-5x+by = -5x + by=-5x+b. Bereken “bbb”.

6=-5(2)+b6 = -5(2) + b6=-5(2)+b

Oplossen en oplossen voor bbb geeft:

6=-10+b6 = -10 + b6=-10+bb=16b = 16b=16

Bedenk dat bbb ook bekend is als het y-afsnijpunt, dus het y-afsnijpunt is ook 161616!

Richting bepalen uit twee punten

Vraag 10: Gegeven twee punten (6, 1) en (-10, 9), bepaal de helling van de lijn.

Herinner je dat we om de helling van de lijn te vinden, de hellingvergelijking

m=y2-y1x2-x1m = \frac{y_{2} – y_{1}}{x_{2} – x_{1}}m=x2-x1y2-y1

Hieruit volgt bij gebruik van deze formule:

m=9-1-10-6=8-16m = \frac{9 – 1}{-10 – 6} = \frac{8}{-16}m=-10-69-1=-168=1-2= \frac{1}{-2}=-21

Wat nu als we in plaats daarvan de volledige vergelijking van een lijn moeten vinden?

Vergelijking van een rechte gegeven twee punten

Vraag 11: Gegeven twee punten (-6, 1) en (2, 6), vind de vergelijking in de vorm van de helling-aftap.

We proberen eigenlijk de vergelijking te vinden in de vorm van y=mx+by = mx + by=mx+b. Daarvoor moeten we mmm en bbb zoeken.

Herinner u dat we om mmm te vinden de hellingvergelijking gebruiken

m=y2-y1x2-x1m = \frac{y_{2} – y_{1}}{x_{2} – x_{1}}m=x2-x1y2-y1

Hieruit volgt bij gebruik van deze formule:

m=6-12-(-6)=58m = \frac{6 – 1}{2 – (-6)} = \frac{5}{8}m=2-(-6)6-1=8558frac{5}{8}85

Nu hebben we dus de vergelijking

y=58x+by = \frac{5}{8}x + by=85x+b

Nu moeten we op zoek naar bbb. Om bbb op te lossen, kiezen we een van de gegeven punten en voegen dat in de vergelijking. We kunnen dat doen omdat beide punten op de rechte liggen, en elk punt op de rechte zou voldoen aan de vergelijking. Laten we het punt (2, 6) gebruiken. Zie dat:

6=58(2)+b6 = \frac{5}{8}(2) + b6=85(2)+b

Oplossing van bbb geeft:

6=108+b6 = \frac{10}{8} + b6=810+bb=6-108b = 6 – \frac{10}{8}b=6-810b=488-108b = \frac{48}{8} – \frac{10}{8}b=848-810b=388b = \frac{38}{8}b=838

Door dit in decimale vorm te zetten, krijgen we dat b=4,75b = 4,75b=4,75. Onze vergelijking in de vorm van een richtingscoëfficiënt is dus:

y=58x+4.75y = \frac{5}{8}x + 4.75y=85x+4.75

Het laatste wat we in deze sectie moeten behandelen is het vinden van het domein en het bereik van een lijn.

Hoe vinden we domein en bereik?

Om het domein van een lijn te vinden, stellen we ons in feite de volgende vraag: wat kan xxx zijn? Als xxx die waarden kan zijn, dan voegen we ze toe aan het domein.

Hetzelfde geldt voor het bereik. Wat kan yyy zijn? Als yyy deze waarden kunnen zijn, dan voegen we ze toe in het bereik. Laten we een voorbeeld doen.

Vraag 12: Vind het domein en bereik van de vergelijking y=2x+1y = 2x + 1y=2x+1.

Merk op dat als we de grafiek van deze lijn tekenen, we krijgen:

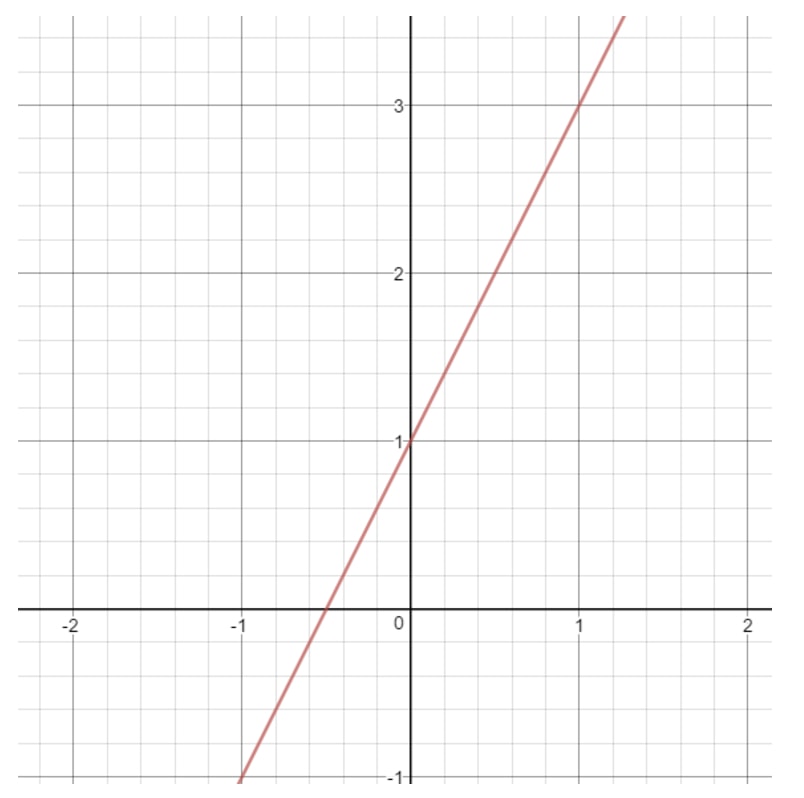
Wat kan xxx in deze lijn zijn? Merk op dat xxx alles kan zijn, want met elke xxx-waarde kunnen we een punt krijgen dat op de lijn ligt. Hetzelfde geldt voor y. We kunnen altijd een yy-waarde kiezen die ons een punt op een lijn oplevert. Dus zeggen we dat

Domain: {x∈∈R}Bereik: {y∈in∈R}

waar R betekent “alle reële getallen”. Laten we een moeilijkere doen.

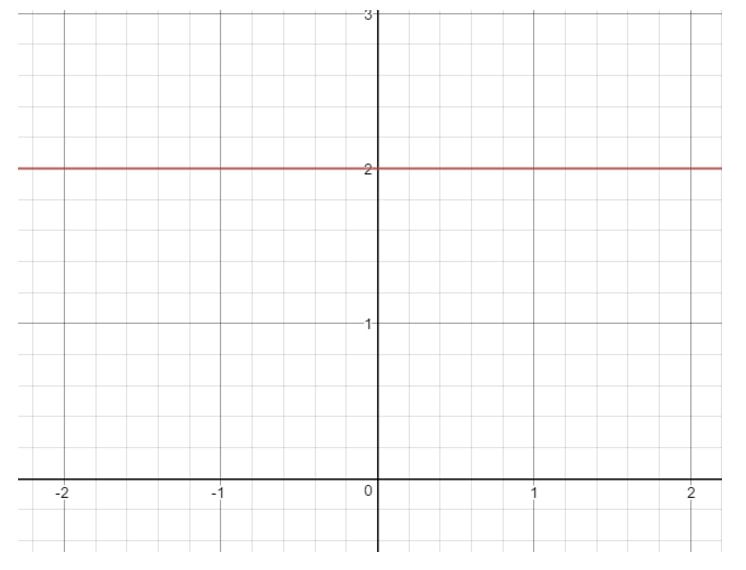
Vraag 13: Vind het domein en bereik van de vergelijking y=-2y = -2y=-2.

Als we nu deze lijn op een grafiek tekenen, krijgen we:

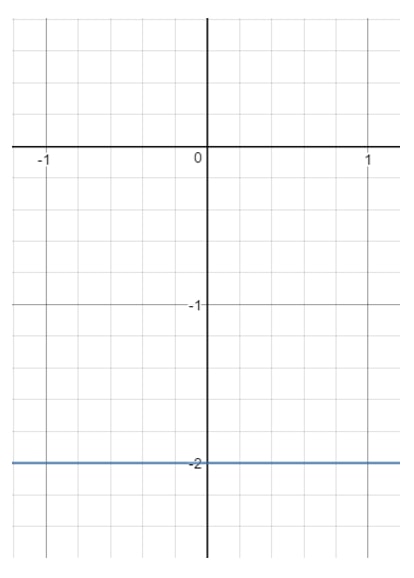
Merk op dat xxx alles kan zijn, want met elke xxx-waarde kunnen we een punt krijgen dat op de lijn ligt, zolang y=-2y = -2y=-2. Kijk echter naar yyy. Je ziet dat yyy gedwongen is tot -2-2-2 en niet iets anders kan zijn. Op het moment dat je een andere yyy waarde kiest (zoals 111), dan zal dat punt buiten de lijn liggen. Dus dat betekent:

Domain: {x ∈in∈ R}Bereik: {y = -2}

Vraag 14: Bepaal het domein en het bereik van de vergelijking x=1x = 1x=1.

Als we nu deze lijn op een grafiek tekenen, krijgen we:

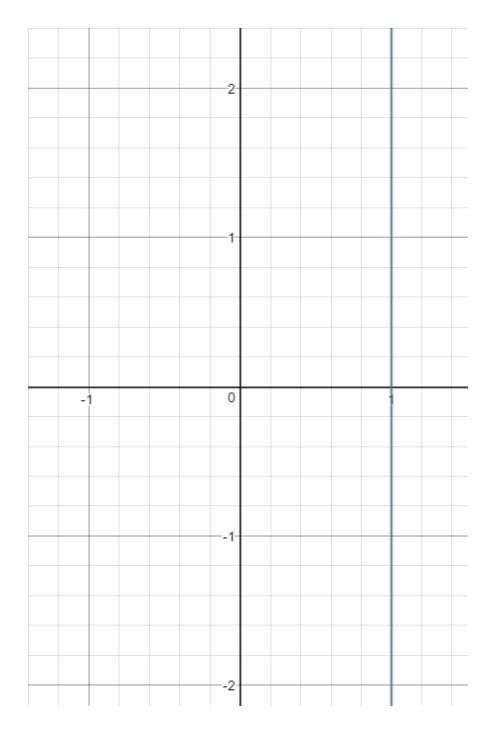
Je ziet dat xxx gedwongen is tot 111 en niets anders kan zijn. Op het moment dat je een andere xxx waarde kiest (zoals 222), dan zal dat punt buiten de lijn vallen.Kijk echter naar yyy. Merk op dat yyy alles kan zijn want met elke yyy waarde kunnen we een punt krijgen dat op de lijn ligt zolang x=1x = 1x=1

Dus dat betekent:

Domein: {x=1}Bereik: {y∈∈R}

Als je veel problemen had met het tekenen van de grafieken om het domein en bereik te verkrijgen, raad ik je aan deze rekenmachine te gebruiken.

https://www.desmos.com/calculator/2rnqgoa6a4

Hiermee leer je hoe je een lineaire vergelijking in een grafiek kunt zetten. Het enige wat je hoeft te doen is de waarden van mmm en bbb in te typen. Dan zal het automatisch de lijn voor je tekenen! Dit is ook handig als je de helling intercept vorm probeert te vinden.