Hoe doen we een Guinier fit?¶
De Guinier benadering gaat alleen op als de exponentiele \(\exp(-q^2 R_g^2 /3)\) klein is. Dit betekent dat om een goede Guinier-benadering te krijgen, weqRg voldoende klein moeten hebben. De qRg-waarde waarbij de Guinier-benadering voor een gegeven verstrooiingsprofiel begint te falen, hangt af van de algemene vorm van de verstrooier. Hieronder staat een figuur met de Guinier-benadering (zwart) en de verstrooiingsintensiteit voor een bol, dunne staaf en dunne schijf (alle met dezelfde Rg).
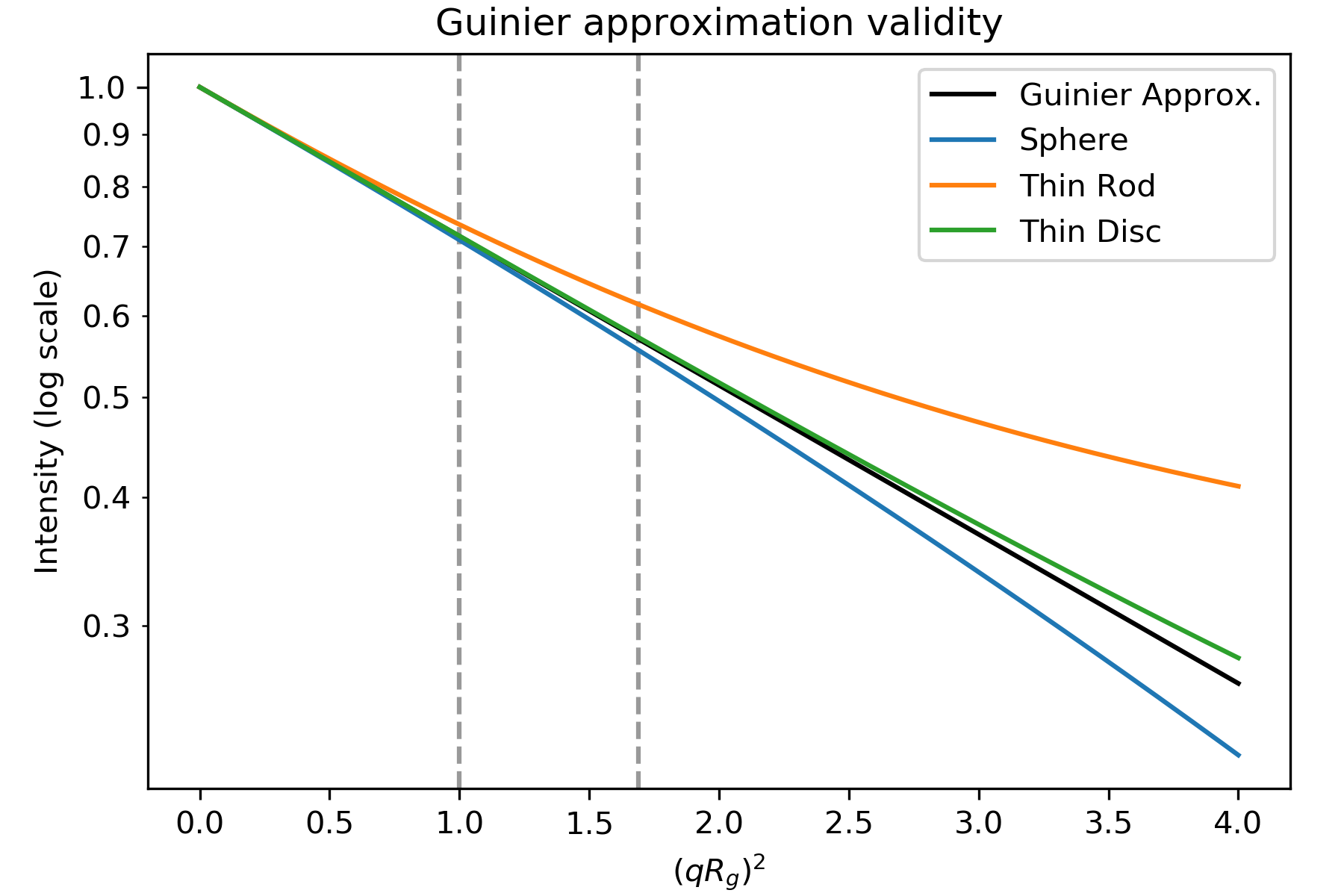
Plot gebaseerd op figuur 3.3 in . Intensiteit voor de geometrische vormen uit tabel 3.4 in . De stippellijnen zijn bij qRg van 1.0 en 1.3 ((qRg) 2 van 1.0 en 1.69).
Zoals u kunt zien, komt de verstrooiingsintensiteit voor de staaf slechts tot aan qR_g\sim 1.0 overeen met de Guinier benadering, de bol tot aan qR_g\sim 1.3, en de schijf tot aan qR_g\sim 1.7. Dus, afhankelijk van de algemene deeltjesvorm, moet u verschillende hoeveelheden van de lage q data passen om een goede Guinier fit te krijgen. (Opmerking: de x-as van de grafiek is (qRg) 2, dus (qR_g\sim 1.3) verschijnt als de stippellijn bij 1.69)
In de praktijk passen we zowel bolvormige (bolvormige en schijfvormige) objecten tot \(qR_g\sim 1.3).terwijl we zeer uitgebreide (staafvormige) objecten passen tot \(qR_g\sim 1.0). Deze waarden zijn zo gekozen dat ze <10% fout hebben als gevolg van de afwijking van de werkelijke vorm van de Guinier benadering. De reden dat we zo’n grote afwijking accepteren is dat je ook onzekerheid krijgt door minder punten in je data te passen, dus er is een afweging tussen hoe goed de benadering werkt (passen op kleinere maximale qRg) en hoe goed je je data kunt passen (passen op grotere maximale qRg).
Het bereik van de Guinier fit is dus idealiter vanaf de vroegst beschikbare q-waarde tot een maximale qRg van 1,0 of 1,3. Echter, gegeven dat Rg is afgeleid van de Guinier fit, hoe bepaal je de juiste maximale q-waarde voor het einde van de fit? Het antwoord is dat de Guinier fit iteratief wordt uitgevoerd:
- Bepaal een beginwaarde voor de maximale q-waarde voor de fit.
- Bereken de Guinier fit en verkrijg Rg.
- Als qmaxRg > 1.3 (of 1.0), verlaag dan de maximum q. AlsqmaxRg < 1.3 (of 1.0), verhoog dan de maximum q.
- Herhaal stap 2 en 3 totdat u convergeert naar een uiteindelijke maximum q.
De meeste software zal tegenwoordig deze iteratieve zoektocht voor u doen, en voor gegevens van goede kwaliteit u een redelijke maximum q-waarde geven die misschien slechts een beetje handmatige verfijning behoeft.
De minimum q-waarde van een Guinier fit wordt gewoonlijk bepaald door de minimum beschikbare q-waarde in uw gegevens, die wordt ingesteld door het instrument waarop u de meting uitvoert.Het is echter belangrijk een minimum q te hebben dat klein genoeg is om een redelijke marge voor de Guinier fit te hebben. Meestal moet de minimale qRg-waarde 0,65% zijn, hoewel het voor bolvormige stelsels goed kan zijn om 1,0% te hebben. Dit betekent dat de minimaal vereiste q-waarde afhangt van de grootte van het gemeten stelsel. In sommige gevallen, met bijzonder grote stelsels, zult u bewust een instrument moeten zoeken dat tot voldoende lage q kan meten.
Als uw gegevens kwaliteitsproblemen hebben bij lage q, die veroorzaakt kunnen worden door de hierboven genoemde problemen, kunt u vinden dat het uitsluiten van die gegevens uit de fit de kwaliteit van de fit kan verbeteren. Hoewel dit acceptabel kan zijn, moet u hierbij voorzichtig te werk gaan en altijd het volledige gegevensbereik op de plots laten zien. Het meest acceptabele geval waarin dit gebeurt is wanneer de eerste paar punten ofwel te hoog ofwel te laag zijn, maar de rest van het bereik perfect past (zie hieronder voor criteria voor een goede fit). In dat geval kunnen de paar punten die het dichtst bij de bundelstop liggen slechte statistieken of hogere instrumentele achtergrondverstrooiing hebben, en kunnen ze meestal veilig worden genegeerd.