Random gebeurtenissen die plaatsvinden in een continue steekproefruimte kunnen om ten minste twee redenen geometrische beelden oproepen: vanwege de aard van het probleem of vanwege de aard van de oplossing.

Sommige problemen, zoals de naald van Buffon, vogels op een draad, de paradox van Bertrand, of het probleem van de stok die in drie stukken breekt, doen zich vanwege hun aard voor in een geometrische setting. Dit laatste probleem kan ook op verschillende manieren worden opgelost, waarbij de oppervlakten van meetkundige figuren moeten worden vergeleken. In het algemeen kunnen wij meetkundige waarschijnlijkheden beschouwen als niet-negatieve grootheden (niet groter dan 1) die volgens bepaalde regels worden toegewezen aan deelgebieden van een bepaald domein. Als de functie μ een uitdrukking is van deze toewijzing, gedefinieerd op een domein D, dan eisen wij bijvoorbeeld

0 ≤ μ(A) ≤ 1, A ⊂ D en
μ(D) = 1

De functie μ is gewoonlijk niet gedefinieerd voor alle A ⊂ D. De deelverzamelingen van D waarvoor μ gedefinieerd is, zijn de toevallige gebeurtenissen die een bepaalde steekproefruimte vormen. Heel vaak wordt μ gedefinieerd door middel van de verhouding van oppervlakten, zodat, als σ(A) wordt gedefinieerd als de “oppervlakte” van verzameling A, men μ(A) = σ(A) / σ(D) kan stellen.

Probleem 1

Twee vrienden die vanaf hetzelfde station de metro naar hun werk nemen, komen uniform willekeurig tussen 7 en 7:20 ’s morgens op het station aan. Ze zijn bereid 5 minuten op elkaar te wachten, waarna ze samen of alleen een trein nemen. Wat is de kans dat zij elkaar op het station ontmoeten?

In een cartesisch coördinatenstelsel (s, t) stelt een vierkant met zijde 20 (minuten) alle mogelijkheden voor van de ochtendaankomsten van de twee vrienden op het metrostation.

Het grijze gebied A wordt begrensd door twee rechte lijnen, t = s + 5 en t = s – 5, zodat binnen A, |s – t| ≤ 5. Hieruit volgt dat de twee vrienden elkaar alleen zullen ontmoeten als hun aankomsten s en t in gebied A vallen. De kans dat dit gebeurt, wordt gegeven door de verhouding van de oppervlakte van A tot de oppervlakte van het vierkant:

/ 400 = 175/400 = 7/16.

Probleem 2

(.)

Drie punten A, B, C worden willekeurig op een cirkel met straal 1 geplaatst. Hoe groot is de kans dat ΔABC scherp is?

Vast punt C. De posities van de punten A en B worden dan bepaald door bogen α en β die zich vanuit C in twee richtingen uitstrekken. A priori weten we dat 0 < α + β < 2π. De voor ons probleem gunstige waarden van α en β (als snijdende scherpe hoeken voldoen) 0 < α < π en 0 < β < π. Hun som kan niet kleiner zijn dan π want dan zou hoek C stom zijn, dus α + β > π. De situatie wordt weergegeven in het volgende diagram waar het vierkant de zijde 2π heeft.

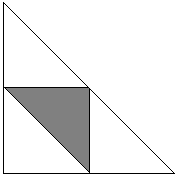
Regio D is het snijpunt van drie halve vlakken: 0 < α, 0 < β, en α + β < 2π. Dit is de grote driehoek in het bovenstaande diagram. De gunstige gebeurtenissen behoren tot de gearceerde driehoek die het snijpunt is van de halve vlakken α < π, β < π, en α + β > π. De verhouding van de oppervlakten van de twee is uiteraard 1/4.

Merk nu op, dat tenzij de willekeurige driehoek scherphoekig is, hij als stomphoekig kan worden beschouwd omdat de kans dat twee van de drie punten A, B, C een middellijn vormen 0 is. (Om BC een middellijn te laten zijn, moet α + β = π, wat een rechte lijn is, met nul als de enige mogelijke toewijzing van oppervlakte). We kunnen dus zeggen dat de kans dat ΔABC stomphoekig is 3/4 is. Voor een stomphoekige driehoek kan de cirkel in twee helften worden verdeeld, waarbij de driehoek volledig in een van de helften ligt. Hieruit volgt dat 3/4 het antwoord is op de volgende vraag:

Drie punten A, B, C worden willekeurig geplaatst op een cirkel met straal 1. Wat is de kans dat ze alle drie in een halve cirkel liggen?

1. E. J. Barbeau, Murray S. Klamkin, W. O. J. Moser, Five Hundred Mathematical Challenges by (MAA, 1995, probleem 244.)
2. D. A. Klain, G.-C. Rota Introduction to Geometric Probability , Cambridge University Press, 1997
3. A. A. Sveshnikov, Problems in Probability Theory, Mathematical Statistics and Theory of Random Functions, Dover, 1978
4. A. M. Yaglom, I. M. Yaglom, Challenging Mathematical Problems With Elementary Solutions, Dover, 1987

Geometric Probability

• Geometric Probabilities
• Are Most Triangles Obtuse?
  • Acht selecties in zes sectoren
  • Drie willekeurige punten op een cirkel
• Geometrische waarschijnlijkheid
  • Stok in drie stukken gebroken (Trilineaire Coördinaten)
  • Stok in drie stukken gebroken. Oplossing in cartesiaanse coördinaten
• Bertrand’s Paradox
• Birds On a Wire (Probleem en Interactieve Simulatie)
  • Birds on a Wire: Oplossing door Nathan Bowler
  • Birds on a Wire. Oplossing door Mark Huber
  • Birds on a Wire: een probabilistische simulatie. Oplossing door Moshe Eliner
  • Birds on a Wire. Oplossing door Stuart Anderson
  • Birds on a Wire. Oplossing door Bogdan Lataianu
• Buffon’s Noodle Simulation
• Het gemiddelde van regendruppels – een oefening in geometrische waarschijnlijkheid
  • Het gemiddelde van regendruppels, deel 2
• Rechthoek op een schaakbord: een inleiding
• Stokjes markeren en breken
• Random punten op een segment
• Semicirkeldekking
• Hemisfeerdekking
• Overlappende willekeurige intervallen
• Random intervallen with One Dominant
• Points on a Square Grid
• Flat Probabilities on a Sphere
• Probability in Triangle

|Contact||Front page||Contents||Up|

Copyright © 1996-2018 Alexander Bogomolny