Statistiekdefinities > Friedman’s Test
Wat is Friedman’s Test?
Friedman’s test is een niet-parametrische test voor het vinden van verschillen in behandelingen over meerdere pogingen. Niet-parametrisch betekent dat de test er niet van uitgaat dat de gegevens uit een bepaalde verdeling komen (zoals de normale verdeling). In principe wordt hij gebruikt in plaats van de ANOVA-test wanneer u de verdeling van uw gegevens niet kent.
De test van Friedman is een uitbreiding van de tekentest, die wordt gebruikt wanneer er meerdere behandelingen zijn. In feite zijn de twee toetsen identiek als er slechts twee behandelingen zijn.
Uitvoeren van de toets
Uw gegevens moeten aan de volgende eisen voldoen:
- De gegevens moeten ordinaal zijn (bijv. de Likert-schaal) of continu,
- Gegevens zijn afkomstig van één groep, gemeten bij ten minste drie verschillende gelegenheden,
- De steekproef is tot stand gekomen met een aselecte steekproefmethode,
- Blocks zijn onderling onafhankelijk (d.d.w.z. alle paren zijn onafhankelijk – het ene beïnvloedt het andere niet),
- waarnemingen zijn gerangschikt binnen blokken zonder gelijken.
De nulhypothese voor de test is dat de behandelingen allemaal identieke effecten hebben, of dat de steekproeven op de een of andere manier verschillen. Bijvoorbeeld, ze hebben verschillende centra, spreidingen, of vormen. De alternatieve hypothese is dat de behandelingen wel degelijk verschillende effecten hebben.
Voorbereid uw gegevens voor op de test.
Stap 1: Sorteer uw gegevens in blokken (kolommen in een spreadsheet).Voor dit voorbeeld hebben we 12 patiënten die drie verschillende behandelingen krijgen.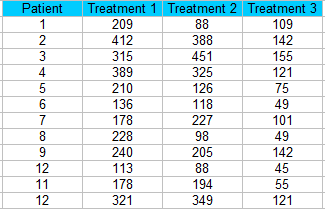
Stap 2: Rangschik elke kolom afzonderlijk. De kleinste score moet een 1 krijgen. Ik rangschik hier over de rijen heen, dus elke patiënt krijgt een 1, 2 of 3 voor elke behandeling.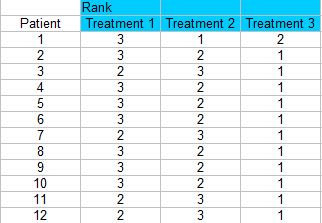
Stap 3: Tel de rangschikkingen bij elkaar op (vind een totaal voor elke kolom).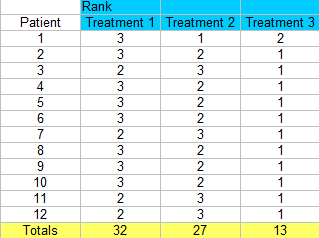
Uitvoeren van de test
Noot: deze test wordt gewoonlijk niet met de hand uitgevoerd, aangezien de berekeningen tijdrovend en arbeidsintensief zijn. Bijna alle populaire statistische softwarepakketten kunnen deze test uitvoeren. Ik vermeld hier echter de handmatige stappen ter referentie.
Stap 4: Bereken de teststatistiek. U hebt nodig:
- n: het aantal proefpersonen (12)
- k: het aantal behandelingen (3)
- R: de totale rangschikking voor elk van de drie kolommen (32, 27, 13).
Voeg deze in de volgende formule in en los op: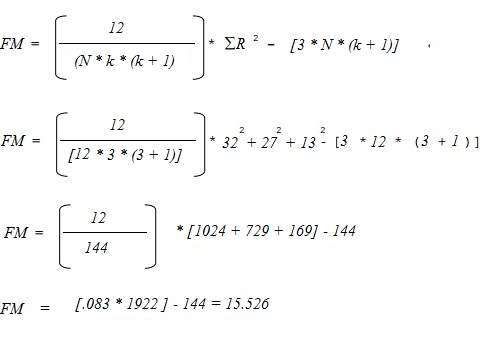
Stap 5: Zoek de kritieke waarde FM uit de tabel met kritieke waarden voor Friedman (zie tabel hieronder).
Gebruik de tabel met k=3 (want zoveel behandelingen hebben we) en een alfaniveau van 5%. U kunt een hoger of lager alfaniveau kiezen, maar 5% is vrij gebruikelijk – gebruik dus de 5%-tabel als u uw alfaniveau niet kent.
Als we n-12 in die tabel opzoeken, vinden we een FM-kritieke waarde van 6,17.
Stap 6: Vergelijk de berekende FM-teststatistiek (stap 4) met de FM-kritieke waarde (stap 5). Verwerp de nulhypothese als de berekende F-waarde groter is dan de FM-kritieke waarde.:
- Berekende FM-teststatistiek = 15,526.
- Kritieke waarde uit tabel = 6,17.
De berekende FM statistiek is groter, zodat u de nulhypothese zou verwerpen.
Friedman’s ANOVA by Ranks Critical Value Table
Drie tabellen volgens “k”.
Als uw k groter is dan 5, of uw n groter dan 13, gebruik dan de chi kwadraat kritische waardetabel in stap 5 om de kritische waarde te krijgen.
k=3
| N | α <.10 | α ≤.05 | α <.01 |
| 3 | 6.00 | ||
| 4 | 6.50 | 8.00 | |
| 5 | 5.20 | 6.40 | 8.40 |
| 6 | 5.33 | 7.00 | 9.00 |
| 7 | 5.43 | 7.14 | 8.86 |
| 8 | 5.25 | 6.25 | 9.00 |
| 9 | 5.56 | 6.22 | 8.67 |
| 10 | 5.00 | 6.20 | 9.60 |
| 11 | 4.91 | 6.54 | 8.91 |
| 12 | 5.17 | 6.17 | 8.67 |
| 13 | 4.77 | 6.00 | 9.39 |
| ∞ | 4.61 | 5.99 | 9.21 |
k=4
| N | α <.10 | α ≤.05 | α <.01 |
| 2 | 6.00 | – | |
| 3 | 7.40 | 8.60 | |
| 4 | 6.30 | 7.80 | 9.60 |
| 5 | 6.36 | 7.80 | 9.96 |
| 6 | 6.40 | 7.60 | 10.00 |
| 7 | 6.26 | 7.80 | 10.37 |
| 8 | 6.30 | 7.50 | 10.35 |
| ∞ | 6.25 | 7.82 | 11.34 |
k=4
| N | α <.10 | α <.01 | |
| 3 | 7.47 | 8.53 | 10.13 | 4 | 7.60 | 8.80 | 11.00 | 5 | 7.68 | 8.96 | 11.52 | ∞ | 7.78 | 9.49 | 13.28 |
Reference:
Friedman’s Two-way Analysis of Variance by Ranks – Analysis of k-Within-Group Data with a
Quantitative Response Variable. Retrieved 7-17-2016 from: http://psych.unl.edu/psycrs/handcomp/hcfried.PDF
Stephanie Glen. “Friedman’s Test / Two Way Analysis of Variance by Ranks” Van StatisticsHowTo.com: Elementaire Statistiek voor de rest van ons! https://www.statisticshowto.com/friedmans-test/
——————————————————————————
Heb je hulp nodig bij een huiswerk- of toetsvraag? Met Chegg Study kunt u stap-voor-stap oplossingen voor uw vragen krijgen van een expert op dit gebied. Uw eerste 30 minuten met een Chegg-leraar zijn gratis!