Hoeveel weet jij over oneindigheden? Je hebt vast wel eens gehoord van een getal dat het grootst mogelijke getal is, of onmogelijk groot.
Om oneindigheden uit te leggen, moet ik eerst wat terminologie definiëren.
Geheelgetallen zijn getallen die gebruikt worden om te tellen. De verzameling gehele getallen wordt gedefinieerd als alle getallen zonder breukdelen. Enkele voorbeelden zijn: -12, 0, 1, 3, 42, 17.
Infiniteit is het concept van een object buiten het bereik van de natuurlijke getallen. Het werd voor het eerst geconceptualiseerd door een Russische wiskundige genaamd Georg Cantor, die niet alleen oneindigheid introduceerde, maar ook onthulde dat er meerdere oneindigheden bestonden.
Cantor leverde een controversieel bewijs van oneindigheden, waarin stond dat sommige oneindigheden groter waren dan andere. Op het eerste gezicht lijkt dit onmogelijk: hoe kan een object groter zijn dan een ander object dat oneindig is?

Cantor baseerde zijn bewijs op een tak van de wiskunde die schijnbaar nutteloos is: Set Theorie. Een set is een verzameling objecten – we kunnen bijvoorbeeld een set hebben die 1, 2 en 3 bevat. Deze objecten in de verzameling worden elementen genoemd.
In wiskundige notatie zou dit er als volgt uitzien:
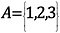
Het aantal elementen in deze verzameling, of de kardinaliteit van de verzameling, is 3.
Dit wordt aangeduid als:
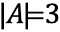
Als we nu een andere verzameling hebben, B, die voorwerpen bevat, zodanig dat
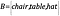
Hoe weten we dan dat de verzamelingen dezelfde grootte hebben?
Een manier om dit te zien is door het aantal elementen in de tweede verzameling te tellen. We kunnen duidelijk zien dat deze set ook 3 elementen bevat, en dus weten we dat ze even groot zijn.
Een andere manier waarop we dit kunnen doen is door onze tweede set, B, te vergelijken met onze eerste set, A door mapping.
We kunnen het eerste element van set A , 1, mappen naar het eerste element van set B, stoel.
We kunnen het tweede element uit verzameling A , 2, mappen naar het tweede element van verzameling B, tafel.
We kunnen het derde element uit verzameling A , 3, mappen naar het derde element van verzameling B, hoed.
Omdat elk element uit A wordt gemapt op precies 1 element uit B, zijn de verzamelingen even groot.
Laten we nu eens kijken naar oneindige verzamelingen. De verzameling gehele getallen, die in het begin werd genoemd, is een oneindige verzameling – er zijn oneindig veel gehele getallen. De verzameling gehele getallen wordt aangeduid met het symbool
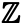
De verzameling van even getallen, die we kunnen aanduiden als

is gedefinieerd als
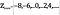
Intuïtief, kan het lijken alsof
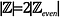
want er zijn 2 gehele getallen voor elk even geheel getal: 1 oneven geheel getal en 1 even geheel getal. Laten we dit verifiëren.
Laten we proberen de verzamelingen te vergelijken door elementen van de ene verzameling naar de andere te mappen.
We kunnen 1 naar 2 mappen, 2 naar 4, 3 naar 6, enzovoort.
Als we zo door de verzamelingen heen gaan, zien we dat elk element uit de gehele verzameling overgaat in precies 1 element uit de even gehele verzameling.
Dus, al lijkt het tegen-intuïtief, de grootte van de verzamelingen zijn gelijk.