分散は、数字の集合がどのくらい離れているかを示す数字です。
分散 – 例
ある研究で、100人が80回の試行で簡単なスピードの課題を実行しました。 こうして各参加者について、80回の反応時間(秒単位)が記録される。 5007> 
このような研究では、通常、速度課題をより頻繁に実行すると、人々がより速くなることがわかります。 つまり、平均反応時間は試行回数が増えるにつれて短くなる傾向がある。
また、反応時間は通常、タスクをより頻繁に実行する限り、異なる人々の間であまり変化しない。 専門的には、試行回数が増えるにつれて分散が小さくなることを言います。 以下の表は、試行1、4、7、10についてこれを示しています。
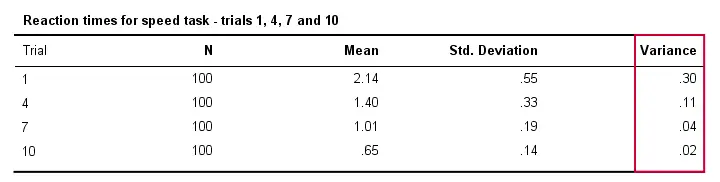
Variance and Histogram
前の表からデータを視覚化する素晴らしい方法は、各試行についてのヒストグラムです。 試行 1 から試行 10 まで、ヒストグラム バーは左方向、0 秒に向かって移動します。
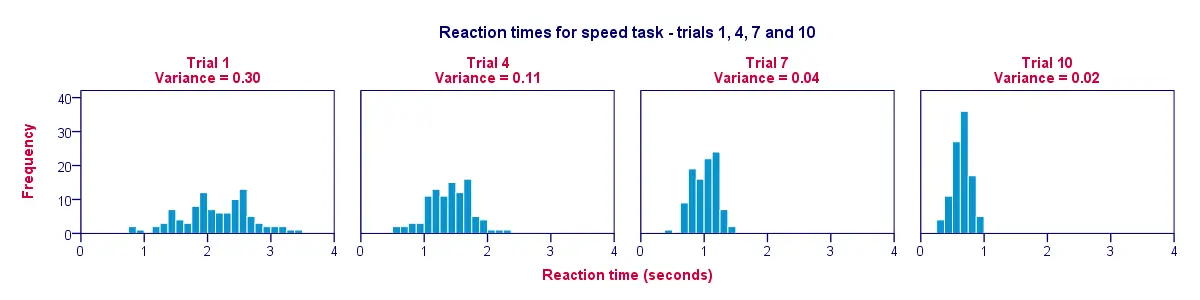
2 番目の発見は、試行 1 から試行 10 に移動するとヒストグラムが狭くなる (従って高くなる) ことで、これは、実験が進むにつれて被験者間の反応時間が少なくなっていることを表しています。 5007>
Variance – Population Formula
分散の基本的な計算式は
$S^2 = \frac{sum(X – \overline{X})^2}{n}$
この式が何をするか理解しておくと、 ANOVA (= Analysis of variance) を理解するのに大いに役立つでしょうから、ぜひ挑戦することをお勧めします。 5007>
Variance – GoogleSheets
簡単のために、最初の5人の参加者の最初のトライアルにデータを切り詰めます。 5007> 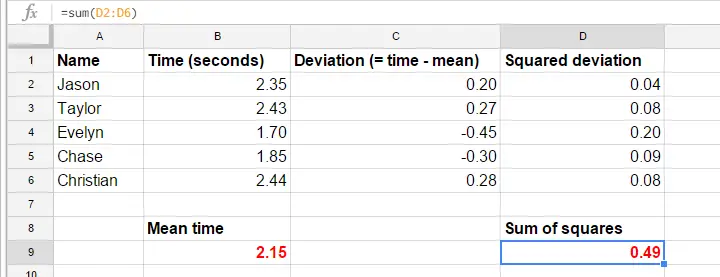
Variance – Calculation Steps
GoogleSheetの公式は、分散の計算方法を正確に示しています。 基本的な手順は、
- 平均反応時間 (2.15) を計算し、
- 偏差値 (反応時間-平均反応時間) を計算し、
- 偏差値の二乗を計算し、
- 偏差値の二乗を追加します。 結果 (0.49) はANOVAの主な構成要素である平方和です。
- 平方和をオブザベーションの数(5つの反応時間)で割ります。
あるいは、いくつかのセル(B2:B6は5つの反応時間を保持しているセル)で=VARP(B2:B6)と入力することによって分散を計算してみてください。 VARPは「分散母集団」の略です。 5007>
分散 – サンプル数式
標準偏差と同様に、データがより大きな母集団からの単純な無作為標本である場合、前述の数式は体系的に母分散を過小評価することになります。 5007>
$S^2 = \frac{sum(X_i – \overline{X})^2}{n – 1}$
どちらの式を使用するかは、調査したい集団全体を含むか、集団からの単なるサンプルか、によって決まります。 5007>
Variance in SPSS
私たちが知る限り、母集団の分散の公式はSPSSには全くなく、これは重大な欠陥であると考えます。 これは被験者間の分散(このチュートリアルで説明)と同様に被験者内の分散にも当てはまります。 5007> 
この出力表に関して、分散は確かに二乗標準偏差(丸めは別として)であることにも注意してください。 このチュートリアルが、分散が何であるかを理解するのにお役に立てれば幸いです。