不要な畳み込みは、アナログ情報の転送に固有の問題である。 例えば、手ぶれカメラの画像ブレ、長距離電話のエコー、アナログセンサーや電子機器の無限の帯域幅など、すべて畳み込みとしてモデル化することができるのです。 デコンボリューションは、望ましくないコンボリューションを補正するために信号をフィルタリングするプロセスである。 デコンボリューションの目標は、コンボリューションが起こる前に存在していた信号を再現することです。 このためには、通常、コンボリューションの特性(すなわち、インパルスまたは周波数応答)を知っていることが必要です。 これは、寄生畳み込みの特性がわからないブラインド・デコンボリューションと区別することができます。 デコンボリューションは、時間領域ではほとんど理解できないが、周波数領域では非常に簡単である。
デコンボリューションは、時間領域ではほとんど理解できませんが、周波数領域では非常に簡単です。元の信号を構成する各正弦波は、望ましくないコンボリューションを通過する際に振幅や位相を変化させることができます。 元の信号を取り出すには、デコンボリューション・フィルターがこれらの振幅と位相の変化を元に戻さなければなりません。
例えば、コンボリューションが 30 度の位相変化で正弦波の振幅を 0.5 だけ変化させる場合、デコンボリューション フィルターは-30 度の位相変化で正弦波を 2.0 だけ増幅させなければなりません。 図17-3に示すように、この装置はシンチレータと光検出器の2つの部分から構成されています。 シンチレータはヨウ化ナトリウムやゲルマン酸ビスマスなどの特殊な透明材料です。 これらの化合物は、ガンマ線のエネルギーを短時間の可視光線に変化させます。 この光は
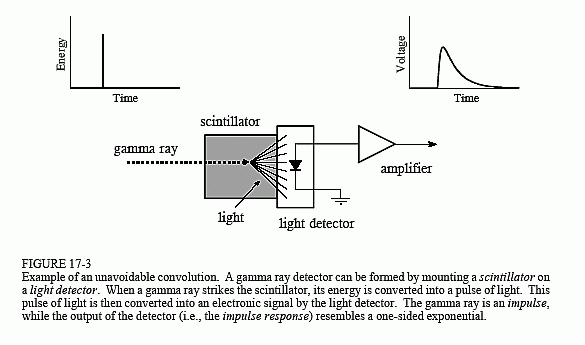
そして、フォトダイオードや光電子増倍管などの光検出器によって電子信号に変換されるのです。 検出器によって生成された各パルスは、角が丸くなった片側指数関数に似ています。 この形状は、使用するシンチレータの特性によって決定されます。 アガンマ線がシンチレータに入射すると、近くの原子はより高いエネルギー準位に励起されます。 これらの原子はランダムに励起され、それぞれ可視光の1光子を発生させます。 その結果、光パルスの振幅は数百ナノ秒かけて減衰する(ヨウ化ナトリウムの場合)。 各ガンマ線の到着はインパルスであるため、検出器からの出力パルス(すなわち片側指数関数)はシステムのインパルス応答となります。
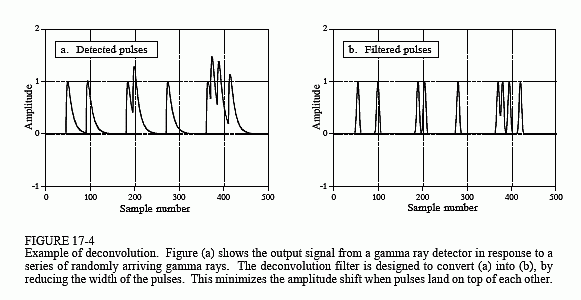
図17-4aはランダムに到来するガンマ線に応答して検出器が生成するパルスを示したものです。 この出力信号から引き出したい情報は、各パルスの振幅で、これはそれを発生させたガンマ線のエネルギーに比例します。 このエネルギーは、ガンマ線がどこに来たかについて興味深いことを教えてくれるので、有用な情報です。 例えば、患者の医療情報を提供したり、遠くの銀河の年齢を教えたり、航空会社の荷物の中にある爆弾を検出したりすることができます。
ガンマ線が時々検出されるだけなら、すべてがうまくいくのですが、通常はそうではありません。 (a)に示すように、2つ以上のパルスが重なり、測定された振幅がずれることがあるのです。 この問題を解決するには、検出器の出力信号をデコンボリューションして、パルスの幅を狭くし、重なりが少なくなるようにすることです。 理想は、各パルスが元のインパルスに似ていることです。 しかし、これは不可能で、有限の長さでありながら、検出されたパルスよりかなり短いパルスにせざるを得ません。 この目標を図17-4bに示します。
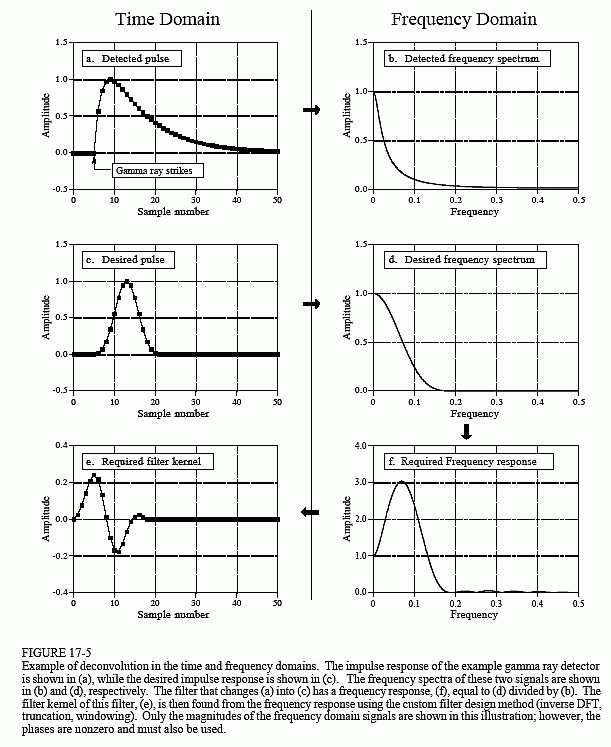
検出信号は時間領域で情報が符号化されていますが、分析の多くは問題を理解しやすい周波数領域で行う必要があります。 図17-5aは検出器によって生成された信号です(私たちが知っているもの)。 図(c)は、私たちが望む信号です(これも分かっていることです)。 この希望するパルスは、ブラックマン窓と同じ形状で、長さは元のパルスの3分の1程度と任意に選択した。 我々の目標は、(a)の信号と畳み込んだときに(c)の信号を生成するフィルターカーネル(e)を見つけることである。 方程式で言うと、a * e = c で、aとcが与えられたら、eを見つけます。
もしこれらの信号がコンボリューションの代わりに加算や乗算で結合されていたら、解決は簡単でしょう。 コンボリューションは違います。”デコンボリューション “と呼べるような単純な逆演算は存在しません。 コンボリューションは、時間領域の信号を直接操作することによって元に戻すことができないほど厄介なものです。
幸いなことに、この問題は周波数領域ではより単純です。 一方の領域での畳み込みは、他方の領域での乗算に対応することを思い出してください。 再び図17-5の信号を参照して、b×f=dとすると、bとdを与えてfを求めます。これは簡単な問題で、フィルタの周波数応答(f)は、目的のパルスの周波数スペクトル(d)を検出パルスの周波数スペクトル(b)で割ったものです。 検出されたパルスは非対称であるため、位相はゼロではありません。 このため、複素分割(つまり、大きさ<2420>の位相を別の大きさ<2420>の位相で割ること)をしなければならない。 第9章でスペクトルの複素分割の方法を説明します。 必要なフィルタカーネル(e)は、カスタムフィルタ法(IDFT, shift, truncate, &multiply by a window)によって周波数応答から求められる。
デコンボリューションがもたらす改善には限度がある。 つまり、欲張ると破綻してしまうのです。 この例で欲張るとは、目的のパルスを過剰に狭くしようとすることです。 どうなるか見てみましょう。 目的のパルスを細くすると、その周波数スペクトルは高周波成分を多く含むはずです。 この高周波成分は、検出されたパルスの中では非常に小さい振幅であるため、フィルタはこの周波数で非常に高い利得を持つ必要があります。 例えば、(f)を見ると、(c)のようなパルスを得るためには、ある周波数を3倍する必要があることがわかります。 また、パルス幅を狭くする場合、デコンボリューションフィルタの利得は高周波数でさらに大きくなる。
問題は、このような場合、小さな誤差は非常に容赦がないことです。 例えば、ある周波数が28だけ必要なときに30だけ増幅されると、デコンボリューションされた信号はおそらくめちゃくちゃになります。 デコンボリューションをより高度な性能にするためには、不要なコンボリューションの特性をより正確に理解する必要があります。 現実のアプリケーションでは、電子ノイズ、温度ドリフト、デバイス間のばらつきなど、常に未知数な部分が存在します。 たとえ不要畳み込みが完全に理解できたとしても、デコンボリューションの性能を制限する事実、すなわちノイズが存在するのです。 例えば、ほとんどの不要な畳み込みはローパスフィルタの形をとり、信号の高周波成分の振幅を減少させます。 デコンボリューションは、これらの周波数成分を増幅することでこれを補正します。 しかし、これらの成分の振幅がシステムの固有ノイズ以下になると、これらの周波数に含まれる情報が失われてしまいます。 いくら信号処理を施しても、その情報を取り戻すことはできません。 永遠に消えてしまうのです。 アディオス!(Adios! さようなら! サヨナラ! このデータを再生しようとしても、ノイズが増幅されるだけです。 極端な例として、いくつかの周波数の振幅が完全にゼロになることがあります。 これは情報を消してしまうだけでなく、デコンボリューションフィルターの利得をその周波数で無限大にしようとする。 解決策: より攻撃的でないデコンボリューション・フィルターを設計し、または、どの周波数でも利得がどの程度まで許容されるかに制限を設ける。
どこまでできるのか? どの程度まで欲張りすぎでしょうか。 これは、あなたが攻撃している問題に完全に依存します。 信号の振る舞いが良く、ノイズが少ない場合、おそらく大幅な改善が可能です (5-10倍を考えてください)。 信号が時間とともに変化し、特によく理解されておらず、ノイズが多い場合は、ほぼうまくいきません(1~2倍とお考えください)。 デコンボリューションを成功させるには、多くのテストが必要です。 ある程度うまくいったら、もっと遠くまで行ってみてください。 どんなに理論的に研究しても、この反復プロセスを回避することはできない。
デコンボリューションは、周波数領域で符号化された信号にも適用できます。 古典的な例としては、有名なオペラ歌手であるエンリコ・カルーソ(1873-1921)の古い録音の復元があります。 これらの録音は、現代の基準からすると非常に原始的な装置で行われたものです。 最も大きな問題は、集音に使われる長い筒状のレコーディングホーンの共振である。 歌い手がこの共振周波数にぶつかると、録音の音量が急激に大きくなってしまうのだ。 デジタル・デコンボリューションは、
音楽中のラウドスポットを減少させることによって、これらの録音の主観品質を向上させたのである。 ここでは、一般的な方法のみを説明し、詳細な説明は原著論文を参照してください。 詳細な説明は原著論文:T. Stockham, T. Cannon, andR. Ingebretsen, “Blind Deconvolution Through Digital Signal Processing”, Proc. IEEE, vol.63, Apr. 1975, pp.678-692.
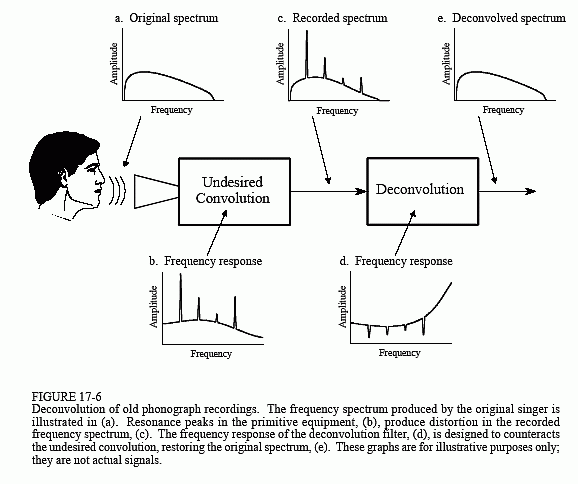
図17-6は、一般的なアプローチを示しています。 (a)は元のオーディオ信号の周波数スペクトルを示している。 (b)は録音機器の周波数特性で、いくつかの鋭い共振ピークを除いて比較的滑らかな曲線である。 録音された信号のスペクトルは(c)のように、(a)の真のスペクトルに(b)の不均一な周波数応答を乗じたものとなる。 デコンボリューションの目的は、望ましくないコンボリューションを打ち消すことである。 つまり、デコンボリューションフィルタの周波数特性(d)は、(b)の逆数でなければならない。 つまり、(b)の各ピークは(d)の対応するディップでキャンセルされる。 このフィルターが完璧に設計されていれば、得られる信号のスペクトル(e)は元の信号と同じになるはずです。
ここで問題なのは、元の録音機材が長い間廃棄されており、その周波数特性(b)が謎であることです。 つまり、これはブラインド・デコンボリューションの問題で、(c)だけがあれば、(d)はどのように決定すればよいのでしょうか。
ブラインドデコンボリューション問題は、通常、未知のパラメータについて推定や仮定をすることで攻略します。 この例では、原曲の平均スペクトルが、現代の歌手が最新の機器を用いて演奏した同じ曲の平均スペクトルと一致すると仮定します。 平均スペクトルは、第9章の手法で求めます:信号を多数のセグメントに分割し、各セグメントをDFTし、極座標に変換し、その大きさを平均化します。 最も単純なケースでは、未知の周波数応答は、古い録音の平均スペクトルを現代の録音の平均スペクトルで割ったものとみなされます。 (Stockhamらが用いた方法は、同型処理と呼ばれるより高度な技術に基づいており、録音システムの特性をよりよく推定することができる)。