物体を吊るすロープの張力の計算方法

下の図を見ると、物体を持ち上げるために必要な力Fは、物体の重量Wと同じであることがわかります。 この考え方は、引張力の公式の根底にある基本的な考え方です。 また、下の図は、物体の自由体図ですが、これはひもに働く引張力Tを表しています。 9573>

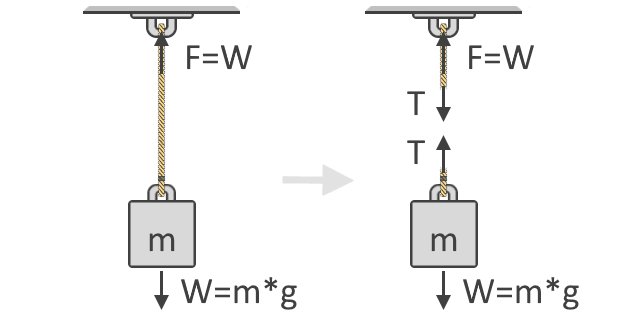
Following the Second Law of Motion, then we can express the sumation of forces using the free-body diagram of the object, as shown at the right side of the above illustrations.ニュートンの第二法則によれば、力の和を、右側のように物体図（FB）を使って表現することができます。 自由体図とは、物体に働く力の方向と大きさの違いを表すものです。 平衡状態では、これらの力はすべてゼロに等しくなるはずです。 上向きの力を正、下向きの力を負とすると、

ΣF = 0 = T + (-W)
T = W
ここで重量Wは下向きなので負になります。 Wを式の反対側に移すと、上でも示したように、ロープの張力は運ぶ物の重さに等しいことがわかります。

物を持ち上げるのにもっとロープを使うと、総張力はロープに分割されます。 各ロープの引張力は、対抗する力の方向に対する角度に依存します。 このことをさらに理解するために、次のような2本のロープで物体を吊るした自由体図を考えてみましょう。

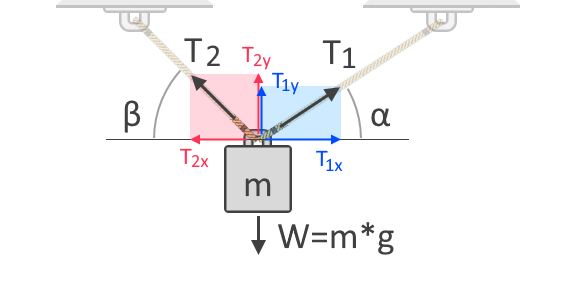
上に示した自由体図で、張力の水平成分と垂直成分 T₁, T₂ を見ることができる。 力はベクトルであり、常に大きさと方向の両方を持つことを意味する。 すべてのベクトルと同様に、力もこれらの成分で表すことができ、水平軸と垂直軸に沿った力の影響を与えることができる。 T₁ₓとT₂ₓは、それぞれT₁とT₂の垂直成分である。 一方、T₁ᵧとT₂ᵧは、それぞれ同じ力の鉛直成分である。 重力は物体に縦軸に作用するので、次のように力の和に引張力の縦成分を考慮する必要がある。

ΣF = 0 = T₁ᵧ + T₂ᵧ + (-W)
W = T₁ᵧ + T₂ᵧ

引張り力の角度も分かっているので、三角関数を用いてT₁ᵧとT₂ᵧをそれぞれT₁とTⅡで表せばいい。

T₁ᵧ = T₁ * sin(α)
T₂ᵧ = T₂ * sin(β)
W = T₁ * sin(α) + T₂ * sin(β)

また、システムが平衡であるためには、物体は水平方向またはx軸方向に動いてはならないと言うことができる。 したがって、そのときT₁とT₂の水平成分はゼロに等しくなければならない。 また、三角測量の助けを借りて、T₁ₓとT₂ₓをそれぞれT₁とT₂で表現することができる。

T₁ₓ = T₂ₓ
T₁ * cos(α) = T₂ * cos(β)

両辺をcos(α)で割ると、T₁をT₂と角で表した式が得られる。

T₁ = T₂ * cos(β) / cos(α)

次にこの式を使って、以下のように力の総和の式のT₁にT₂ * cos(β) / cos(α)を代入してT₂を解くことができる。

W = T₁ * sin(α) + T₂ * sin(β)
W = T₂ * * sin(α) + T₂ * sin(β)
W = T₂ *
T₂ = W /

最後に、この式全体に、T₁の値をTⅡで導いたようにcos(β) / cos(α)をかけて、すべてを単純化するとこの式になる。

T₁ = W / *
T₁ = W / *
T₁ = W /

さて、あとはテンションロープの水平に対する角度だけである。 垂直からの角度が与えられたら、90°からこの角度を引けばよい。 そうすれば、水平からの角度がわかる。 しかし、90°や180°よりも大きな角度の値が与えられた場合は、必要な角度を決定するために、参考となる角度計算機をチェックすることをお勧めします。 引張力の公式で変数の値を決めたら、引張力を求めることができます。