どうやってGuinierフィットをするのか¶
Guinier近似は指数( \exp(-q^2 R_g^2 /3)\ )が小さいときだけ成立します。 つまり、良いGuinierフィットを行うためには、qRgが十分に小さいことが必要です。 ある散乱プロファイルに対してギニエ近似が破綻し始めるqRgの値は、散乱体の全体形状に依存します。 以下は、ギニエ近似(黒)と、球、細い棒、細い円盤(すべて同じRg)の散乱強度を示した図である。
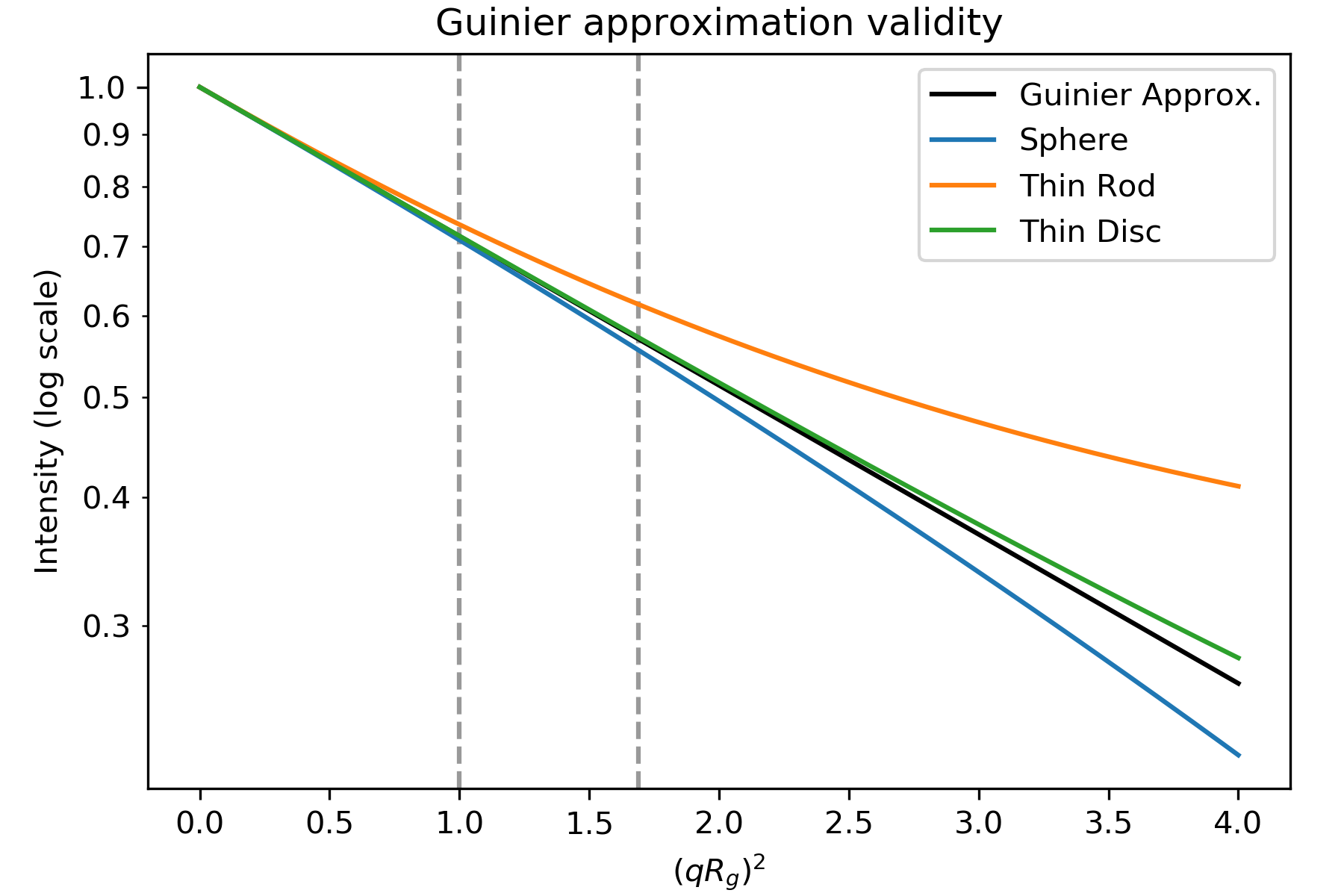
Plot based on Figure 3.3 in . の Table 3.4 からの幾何形状に対する強度を示したもので、図3.4はギニエ近似の結果を示している。 破線はqRgが1.0と1.3((qRg) 2 of 1.0 and 1.69) のとき。
このように、棒の散乱強度がGuinier近似と一致するのは、 \(qR_ggiensim 1.0), the sphere until \(qR_ggiensim 1.3), the disc until \(qR_ggiensim 1.7) までであることが分かる。 このように、全体の粒子形状によって、Guinierフィットを行うために、異なる量のlow qデータをフィットさせる必要があります。 (注:プロットのX軸は(qRg)2なので、1.69の破線に見えるのは \(qR_g} 1.3)
実際には、球状(球状、円盤状)のものは \(qR_g} 1.3 まで、大きく広がった(棒状の)ものは \(qR_g} 1.0 までフィットさせました。 この値は、実際の形状とGuinier近似との乖離による誤差が<10%になるように選んだものです。この程度の乖離を許容する理由は、データ中の少ないポイントにフィットすることによる不確実性も得られるため、近似がうまく機能するか(小さい最大qRgにフィットするか)、データにうまくフィットするか(大きい最大qRgにフィットするか)はトレードオフになるためです。
したがって、Guinierフィットの範囲は、理想的には最も初期の利用可能なq値から1.0または1.3の最大qRgまでである。 しかし、Rgがギニエ・フィットから得られるとすると、フィットの終点となる正しい最大q値をどのように決定するのでしょうか。
- フィットの開始最大q値を求める。
- ギニエフィットを計算し、Rgを得る。
- qmaxRg > 1.3 (または 1.0) なら、最大 q を下げます。
- qmaxRg < 1.3 (または 1.0) なら、最大 q を上げます。最終的に最大 q に収束するまでステップ 2 と 3 を繰り返してください。
ギニエフィットの最小q値は通常、データ中の利用可能な最小q値によって決定され、それは測定を行う機器によって設定されます。 一般的には、qRgの最小値は0.65であるが、球状星系では1.0であっても構わない。 つまり、測定した系の大きさによって、必要なqの最小値は異なるということです。
上記のような低Qでのデータ品質に問題がある場合、フィットからそれらのデータを除外することでフィットの品質が改善されることがあります。 このような場合、最初の数点は高すぎるか低すぎるが、残りの範囲は完全にフィットする場合です(良いフィットの基準については後述)。 この場合、ビームストップに最も近い数点は、統計値が低いか、機器の背景散乱が大きい可能性があり、通常は安全に無視することができる。