ゼロは、数直線上の正の数と負の数のちょうど中間に位置する数です。 0は正の自然数（1、2、3、4…）と負の数（…-4、-3、-2、-1）と共に整数とみなされる。

0は整数の中で特別な数で、正でも負でもない唯一の整数である。 また、素数でも合成数でもない唯一の整数でもある。 2で割っても余りが出ないので偶数であるとみなされる。 ゼロは代数学のさまざまな体系における加法的な同一要素であり、数字を表す位置表記法では数字の「0」がプレースホルダー値として使われる。

ゼロには数学者にとって興味深い特性が多くある。 どんな数でも0を足したり引いたりすると、その数は変わらない。0にどんな数をかけても結果は0である。 0は実数と複素数の要素でもある。

History Of The Number 0

ゼロという概念はどこから来たのだろうか。 現在では直感的に理解できるが、0は無量（何もない状態）を表す数である。 社会のいたるところでゼロを目にし、それが何を意味し、どのように数学的に操作されるかを自然に理解しています。 しかし歴史的には、0という概念が数学の対象として普遍的に認識されるにはかなりの時間がかかり、歴史を通じて多くの人が0という数は存在しない、あるいは0という考えは支離滅裂な概念であると主張しました」

多くの古代社会では、0の量やその表現に使用する特定の桁についての明確な概念を持っていませんでした。 古代エジプト人とバビロニア人は共に、無効な量と、数の表現におけるプレースホルダー値の必要性について何らかの考えを持っていましたが、その量やプレースホルダー値を表す明確な数字や概念を開発することはありませんでした。 5549>

マヤは0という明確な概念を持ち、その概念を表す明確な数字を持ち、20進法のカレンダーシステムでプレースホルダー値として使用した。 マヤ、オルメカ、およびその他の先コロンビア社会は、0 という数について明確かつ洗練された理解を持った歴史上最初の社会のひとつでしたが、これらのシステムは、ヨーロッパの旧世界の社会に影響を与えるまでには至りませんでした。 0という数字が本当に存在するものなのかどうかがわからなかったため、その概念を表す記号も、プレースホルダーとしての値も持たなかったのである。 何か（数）が無（ゼロ）になるとはどういうことなのか。 ギリシャ人にとって、自然数（1、2、3、4、…）は、世界の中の個別の物体を理解することから導き出されたものである。 アリストテレス自身、0は空虚または無を表し、真の空虚または無は存在し得ないという理由で、0は存在しないと主張したのは有名な話だ。

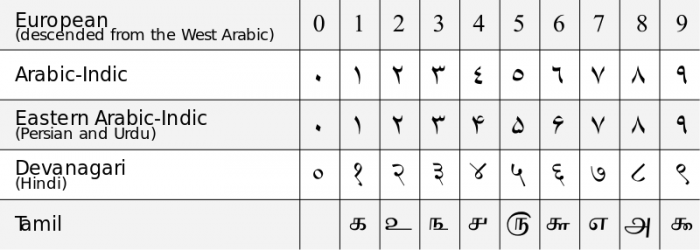
中国では、「0」は数え方のためのプレースホルダとして理解していたが、「0」という桁は、何か別の数を表すものではなく、役に立つ記号に過ぎないと考えていた。 0を数字として、また位置表記のための桁として一般的に理解するようになったのは、西暦6世紀頃のインドからである。 当時のインドの数学者たちは、0を明確な数字として取り入れた最初の10進数表記法を開発し、0が持つユニークな数学的特性を理解していたのだ。 11世紀には、ウマイヤ暦のスペインに住むイスラム数学者の影響で、西ヨーロッパにも「0」の概念が広まり、現在のアラビア数字による10進法が誕生した。 5549>

Mathematical Properties of Zero

数字のゼロは数学のほぼすべての分野で不可欠な役割を担っています。 ゼロは最小の非負の整数で、それに続く自然数を持たない。 0は整数であるため、有理数、実数、複素数でもある。 数学では、0は無量に相当する量と考えられている。 5549>

代数学

初等代数学では、0はしばしば数直線の中心に位置すると表現される。 数0は数2の整数倍（2×0=0）であるため偶数とみなされる。 0は因子が無限にあるため素数ではなく、2つの素数の積が0になることはないため合成数でもない。

四則演算（+、-、×、÷）と指数演算に関して、数0は以下の規則に従って振る舞う：

• 加算： x+0=0+x=x. ゼロは加法恒等式要素とみなされ、ゼロを加えた数、引いた数はその数に等しい
• Subtraction: x-0=x and 0-x=-x
• Multiplication: x⋅0=0⋅x=0.Any number times 0 is also equal to 0.
• Division: 0/x=0, except when x=0. x/0 は数学的に未定義の量であり、0 には乗法的な逆数がない (0 の倍数で 1 になる数はない)。
• Exponents: x0=1, except when x=0. 00 が未定義か正規表現かについては長い議論がある。 すべての正の x に対して、0x=0.

極限を含む式では、f(x)/g(x) のような有理関数の極限を示す文脈で、量 0/0 が現れることがあります。 このような場合、0/0は未定義ではなく、不定形を表す。 これは極限が未定義であるという意味ではなく、微分を求めるなど別の方法で計算しなければならないという意味である。 5549>

集合論

集合論において、数0は「空集合」または「空集合」（一般に{}または{∅}と表される）の基数として対応する。

集合論では、0は残りの自然数を構成するための出発点としてよく使われる。 このフォン・ノイマン構成は、著名な博学者ジョン・フォン・ノイマンにちなんで名付けられたもので、0={}を定義して自然数を構成し、後継関数S（a）=a∪{a}を定義するものである。 自然数の全体は、空集合から始まる後継関数の再帰的な適用から構成することができる。

0 = {}

1 = 0∪{0} = {{}}

2 = 1∪{1} = {0,1} = {{}, {{}}

3 = 2∪{2} = {0,1,2} = {{},{{}},{{}}}

以下となります。 このパターンに従って、自然数の無限集合全体を構成することができる。 5549>

物理学

物理学で定量的な測定を行う場合、0は他のすべての単位の測定が行われる基準であると考えられる。

たとえば、ケルビンスケールでは、0 K の温度は絶対 0-物理的に可能な最も冷たい温度に対応します。 摂氏温度スケールでは、0℃は大気圧での水の凝固点として定義されている。 力学や電磁気学の分野では、ポテンシャルエネルギーが最小になる位置を0とする。 同様に、運動学の文脈では、運動の観測を行う基準フレームは、座標軸の原点を点 (0, 0) に置く中心点を持つものとして定義される。 質量エネルギー、運動量、角運動量などの保存量の場合、孤立した系における保存量への変化の総量は常に0に等しい。

In Computer Science

コンピュータは、ビット長の1と0のシーケンスという形で情報を保存する。 この 2 進表現では、0 は「オフ」位置に対応し、1 で指定された「オン」位置と対照的です。電気回路上の値 0 は、回路がオフで、いかなる電気的フローもないことを意味します。 同様に、多くの計算論理学では「0」を偽の真理値を表す文字と定義している。

コンピュータのデータベースでは、配列の要素は0ベースのカウントシステムを使用してカウントされる。 したがって、インデックス番号 0 の要素は実際には系列の最初の要素であり、インデックス番号 1 は 2 番目の要素に対応し、以下同様である。 一般に、集合の第n項はn-1に対応する添字番号を持つ。 この数え方は、直感的に1から始まるインデックス値を割り当てることに慣れた新米プログラマーを混乱させることがある。