研究において、変数とは、身長、年齢、種、試験のスコアなど、異なる値を取り得るあらゆる特性のことです。
科学研究において、ある変数が別の変数に及ぼす影響を調査したいことがよくあります。 例えば、より多くの時間を勉強に費やす学生は、より良い試験のスコアを得るかどうかをテストしたい場合があります。
因果関係の研究における変数は、独立変数と従属変数と呼ばれます。 その値は、研究の他の変数から独立しています。
| Research Question | 独立変数 | 従属変数 |
|---|---|---|
| トマトが最も速く成長するには蛍光灯、白熱灯、自然光の下だろうか? |
|
|
|
|
|
| 就寝前のスマホ利用が眠りに与える影響とは何ですか? |
|
|
| 異なる植物種はどれくらい塩水に耐えるのか? |
|
|
実験における独立変数と従属変数
実験研究において、「独立した変数」とは? 独立変数が実験者によって操作または変更され、この変化が従属変数に及ぼす影響を測定します。
薬が有効かどうかをテストするために、患者を2つのグループに分けます。
- 独立変数とは、グループ間で変化させる治療法:患者がどのタイプの錠剤を受け取るか、
- 従属変数とは、測定する結果:患者の血圧、
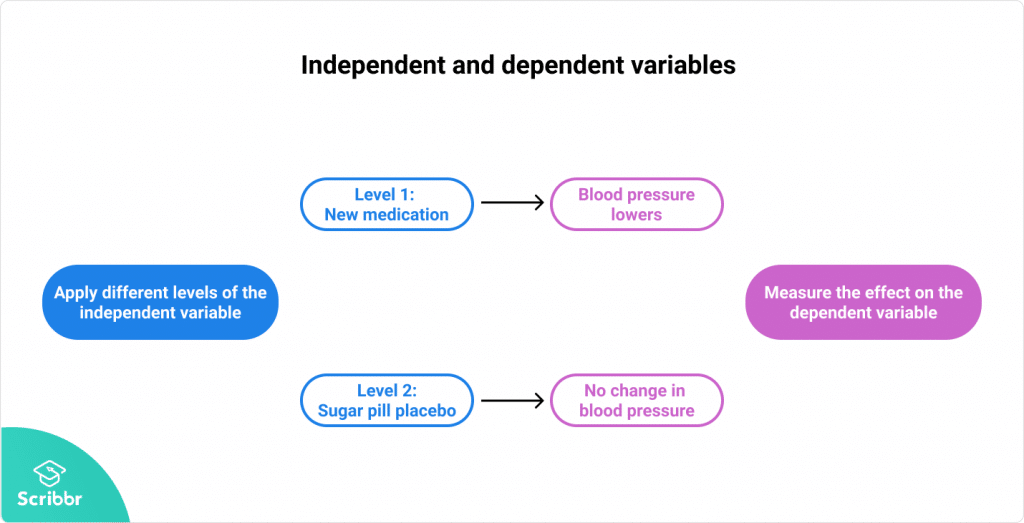
独立変数は通常、結果がどう異なるかを見るために異なるレベルで適用されます。
独立変数が従属変数にどのように影響するかを調べるために、2つのレベル(例:新しい薬とプラセボ)だけを適用することもできます。

他のタイプの研究での変数
実験設定以外では、研究者はしばしば興味のある独立変数を直接操作したり変えたりすることができないことがあります。
その代わり、独立変数のすでに存在する例を見つけ、この変数の変化が従属変数にどのように影響するかを調査しなければなりません。
- 独立変数は最低賃金で、
- 従属変数は雇用率です。
二つの州の結果の違いを比較することによって(と他の要因を考慮)、あなたは最低賃金の変化が雇用率に影響を与えたかどうかを調査することができます。
非実験研究では、あなたが測定していない他の変数が変化に影響を与えているかもしれないので、明確な原因と効果の関係を確立することがより困難です。 これらは交絡変数と呼ばれます。
変数間の正確な関係があまり確かでないタイプの研究では、独立変数と従属変数に異なる用語を使用する場合があります。 この場合、これらの用語のいずれかがより適切です:
- 説明変数(それらはイベントまたは結果を説明します)
- 予測変数(それらは従属変数の値を予測するために使用できます)
- 右辺変数(それらは回帰式の右辺に表示される)。
従属変数の他の名前
従属変数は、これらの用語でも知られています。
- 応答変数(他の変数の変化に応答する)
- 結果変数(測定したい結果を表す)
- 左辺変数(回帰式の左辺に現れる)
独立変数と従属変数の視覚化
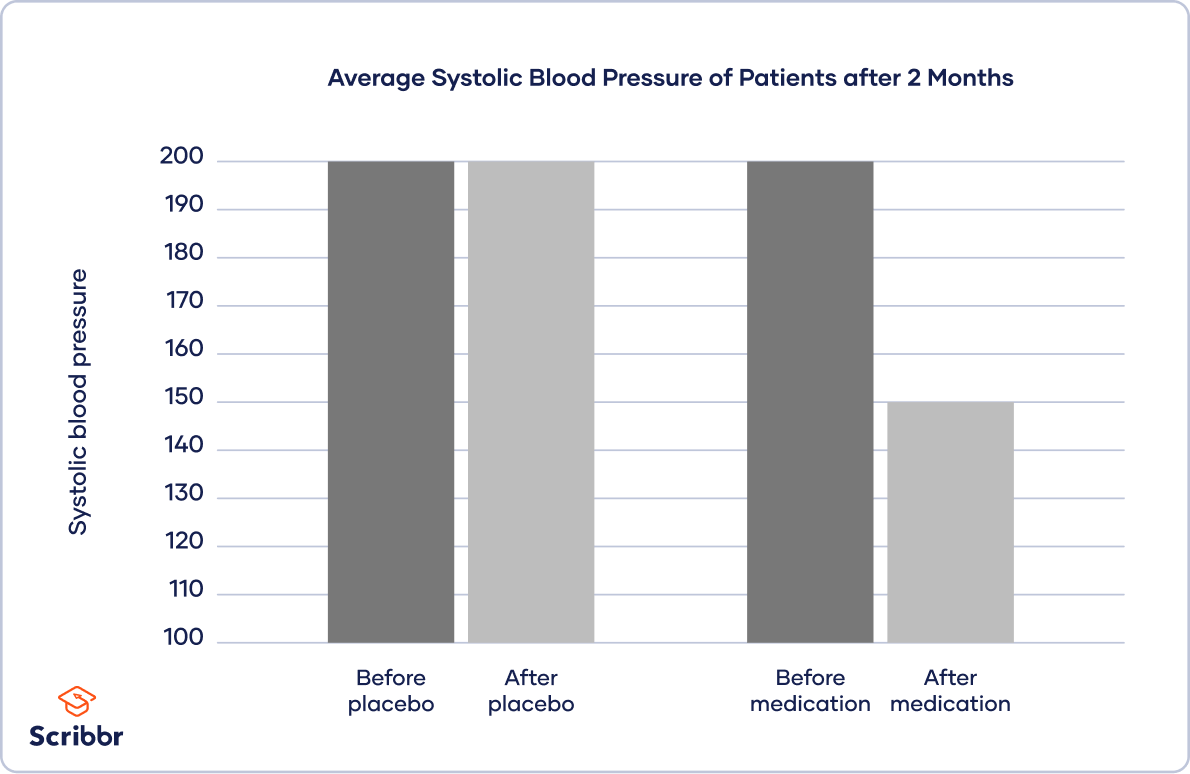
研究者はしばしば図表を使って研究結果を視覚化する。 通常、独立変数を「x」または横軸に、従属変数を「y」または縦軸に配置します。
たとえば、新しい薬の血圧への影響に関する研究例から、グラフはどのように見えるでしょうか。

よくある質問
独立変数と従属変数は、原因と結果で考えることができます。独立変数は原因と考えられる変数で、従属変数は結果です。
実験では、独立変数を操作して、その結果を従属変数で測定します。 例えば、作物の成長に対する栄養素の効果に関する実験では、
- 独立変数は作物畑に加えられた栄養素の量である。
- 従属変数は収穫時の作物のバイオマスである。
変数を定義し、それらをどのように操作し測定するかを決めることは、実験計画の重要な部分です。
原因と結果を決定することは、科学研究の最も重要な部分の1つです。 どちらが原因か-独立変数-、どちらが結果か-従属変数-を知ることが不可欠です。
ダイエットソーダと普通のソーダを飲むと血糖値がどうなるか調べたいので、実験を行います。
- ソーダの種類(ダイエットか普通か)が独立変数にあたります。
- 測定した血糖値が従属変数で、ソーダの種類によって変化します。
いいえ。従属変数の値は独立変数に依存するので、変数は独立変数と従属変数の両方に同時になることはできません。 原因か結果のどちらかでなければならず、両方ではありません!
はい、しかし、どちらかのタイプを複数含めるには、複数のリサーチクエスチョンが必要です。
たとえば、ダイエットの健康への影響に関心がある場合、血糖値、血圧、体重、脈拍など、複数の健康指標を使用することができます。 これらはそれぞれ独自の従属変数であり、独自のリサーチクエスチョンを持ちます。
また、食事だけでなく運動レベルの効果、あるいは2つを組み合わせた付加的な効果に注目することも可能でしょう。 これらはそれぞれ別の独立変数です。
実験の内部妥当性を確保するために、一度に1つの独立変数のみを変更する必要があります。