無限大について、あなたはどれくらいご存知でしょうか？ おそらく、可能な限り大きな数、つまり、ありえないほど大きな数というのを聞いたことがあると思います。

無限を説明するには、まずいくつかの用語を定義しなければなりません。

整数とは数えるために用いられる数のことです。 整数の集合は分数成分を含まないすべての数として定義される。 いくつかの例を挙げます。 -12、0、1、3、42、17。

無限とは、自然数の範囲を超えたものという概念である。 ロシアの数学者ゲオルク・カントールが初めて概念化し、無限を導入しただけでなく、複数の無限が存在することを明らかにしました。

カントールは、ある無限は他の無限より大きいという無限論の証明を行い、論議を呼びました。 最初は、これは不可能に思えるかもしれませんが、ある物体が無限である他の物体よりも大きくなることができるでしょうか。

Cantor は一見役に立たない数学の一分野を基に証明したのです。 集合論です。 集合とは、例えば、1、2、3を含む集合のことである。

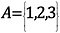
このセットの要素の数、つまりセットの基数は3である。

このように表記される。

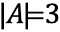
もし今、オブジェクトを含む別の集合Bが、

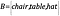
のようになっていたら、どのようにして集合は同じサイズを持っているとわかるのでしょうか。

これを確認する1つの方法は、2番目の集合の要素数を数えることです。

もう1つの方法は、2番目の集合であるBと最初の集合であるAをマッピングで比較することです。

集合Aの2番目の要素を集合Bの2番目の要素であるtableに写像できる。

集合Aの3番目の要素を集合Bの3番目の要素であるhatに写像できる。

Aからのすべての要素はBからのちょうど1つの要素に写されるので、セットサイズは等しい。

ここで無限集合について見てみよう。 冒頭で述べた整数の集合は無限集合であり、整数は無限に存在する。 整数の集合は記号

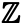
偶数の集合で表される。 であり、これを

と定義する。 2272>

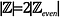
のように見えるかもしれないが、偶数個の整数に対して2個の整数が存在するのである。 奇数整数1個と偶数整数1個です。 これを検証してみましょう。

1つの集合の要素を他の集合に写像して比較してみましょう。

1から2、2から4、3から6、・・・と写像できます。

これをセット全体で行うと、整数セットからのすべての要素は偶数整数セットからのちょうど1つの要素に対応することがわかります。

したがって、直感に反するかもしれませんが、セットの大きさは等しいのです。