by Marco Taboga, PhD
イベントの指標関数は、イベントが起こったときに値1、イベントが起こらなかったときに値0となる確率変数である。

Definition
以下は公式定義である。
定義  をサンプル空間、
をサンプル空間、 を事象とする。
を事象とする。  で示される事象
で示される事象 の指標関数(または指標確率変数)は、次のように定義される確率変数である。
の指標関数(または指標確率変数)は、次のように定義される確率変数である。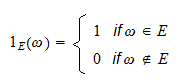
イベント の指標は通常
の指標は通常 で表されるが、
で表されるが、 (
( はギリシャ文字のカイ)で表されることもある。
はギリシャ文字のカイ)で表されることもある。
例題 サイコロを投げて、1から6までの6個の数字のうち1個を表にして出すことができる。 サンプル空間は 「偶数が表向きに出る」という文が記述する事象
「偶数が表向きに出る」という文が記述する事象 を定義する。 偶数が表向きに現れるときに値1、そうでないときに値0をとる確率変数が事象
を定義する。 偶数が表向きに現れるときに値1、そうでないときに値0をとる確率変数が事象 の指標となる。 この指標の場合分けの定義は
の指標となる。 この指標の場合分けの定義は
以上の定義から、 は支持
は支持 と確率質量関数
と確率質量関数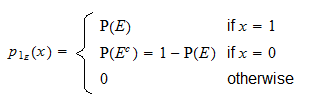
特性
指標関数は以下の特性を楽しむことが簡単に理解できる。
べき乗
 の
の 乗は
乗は と同じである。
と同じである。 なぜなら、
なぜなら、 は
は か
か のどちらかになり、
のどちらかになり、
期待値
 の期待値は
の期待値は と同じになるからです。
と同じになるからです。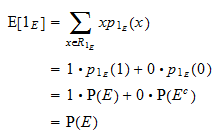
分散
 の分散は
の分散は  に等しい。 通常の分散の公式と上記の累乗の性質のおかげで、
に等しい。 通常の分散の公式と上記の累乗の性質のおかげで、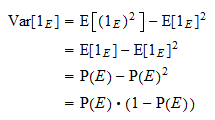
交点
 と
と が二つの事象だとすると、
が二つの事象だとすると、 なぜかというと。
なぜかというと。
-
if
 , then
, then  and
and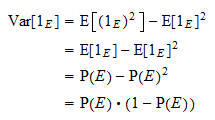
-
if
 , then
, then and
and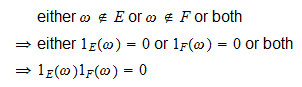
ゼロ確率事象の指標
 をゼロ確率事象、
をゼロ確率事象、 を可積分確率変数とすると、ゼロ確率事象の指標は、
を可積分確率変数とすると、ゼロ確率事象の指標は、 と
と  の間にある。 すると、
の間にある。 すると、 この事実の厳密な証明はこの入門的な解説の範囲を超えているが、この性質は直観的に理解できるはずである。 確率変数
この事実の厳密な証明はこの入門的な解説の範囲を超えているが、この性質は直観的に理解できるはずである。 確率変数 は、おそらくE$” style=”background-position:0px -1174pxvertical-align:-5px”>の点
は、おそらくE$” style=”background-position:0px -1174pxvertical-align:-5px”>の点 で0に等しくなる。 期待値は、
で0に等しくなる。 期待値は、 が取り得る値の加重平均であり、各値はそれぞれの確率で加重されている。 ゼロでない値
が取り得る値の加重平均であり、各値はそれぞれの確率で加重されている。 ゼロでない値 はゼロの確率で重み付けされているので、
はゼロの確率で重み付けされているので、 はゼロでなければならない。
はゼロでなければならない。
練習問題
以下では、練習問題の解答解説をしています。
練習問題1
確率変数  と別の確率変数
と別の確率変数  が
が  の関数として定義されていると考える。
の関数として定義されていると考える。
 を事象
を事象 と
と の指標関数を使って表す。
の指標関数を使って表す。
事象 の指標を
の指標を で、事象
で、事象 の指標を
の指標を であらわし、
であらわし、 とする。
とする。  を
を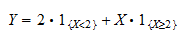
と書くことができる。
演習2
 を正の確率変数、つまり正の値のみを取り得る確率変数とする。
を正の確率変数、つまり正の値のみを取り得る確率変数とする。  を定数とする。
を定数とする。  ここで、
ここで、 は事象
は事象 の指標であることを証明しなさい。
の指標であることを証明しなさい。
まず、指標 と
と の和は常に
の和は常に :
: に等しいことに注意し、その結果として
に等しいことに注意し、その結果として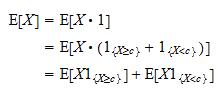 と書くことができる。さて、
と書くことができる。さて、 は正の確率変数であり、正の確率変数の期待値は正であることに注意すること。
は正の確率変数であり、正の確率変数の期待値は正であることに注意すること。 従って、
従って、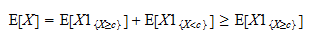
練習問題3
 を事象とし、その指標関数を
を事象とし、その指標関数を とする。
とする。  を
を  の補集合とし、その指標関数を
の補集合とし、その指標関数を  とする。
とする。  を
を の関数として表せるか。
の関数として表せるか。
二つの指標の和は常に :
: に等しいので、
に等しいので、
引用方法
引用元:
Taboga, Marco (2017). “指標関数”, 確率論・数理統計学講義, 第3版. Kindleダイレクト出版. オンライン付録。 https://www.statlect.com/fundamentals-of-probability/indicator-functions.